Sliding DFT-based Signal Recovery for Modulo ADC with 1-bit Folding Information

The modulo analog-to-digital converter (ADC) is a promising solution to resolve the limited dynamic range (DR) issue of conventional ADCs. However, a modulo ADC requires an unfolding scheme to correct the nonlinear distortion introduced by the modulo operation. This paper presents a sliding discrete Fourier Transform (DFT)-based method for fast signal reconstruction given the modulo ADC output sequence and a 1-bit folding information sequence. In contrast to existing DFT-based signal recovery techniques for modulo ADCs, our proposed sliding DFT method reduces the required observation time and minimizes the spectral leakage effects via proper choice of window function parameters. A mean squared error (MSE) performance guarantee is established for the proposed signal recovery algorithm. More precisely, we derive sufficient conditions for the oversampling factor ($\mathrm{OF}$) and the number of quantization bits ($b$) to obtain a specific MSE performance. Our numerical results demonstrate that modulo ADCs equipped with our proposed recovery method can outperform conventional ADCs without modulo for $\mathrm{OF} \geq 4$ and $b \geq 4$. The impact of spectral leakage on the MSE performance of the proposed sliding DFT recovery method is also quantified.

Non-Linear Analog Processing Gains in Task-Based Quantization

In task-based quantization, a multivariate analog signal is transformed into a digital signal using a limited number of low-resolution analog-to-digital converters (ADCs). This process aims to minimize a fidelity criterion, which is assessed against an unobserved task variable that is correlated with the analog signal. The scenario models various applications of interest such as channel estimation, medical imaging applications, and object localization. This work explores the integration of analog processing components -- such as analog delay elements, polynomial operators, and envelope detectors -- prior to ADC quantization. Specifically, four scenarios, involving different collections of analog processing operators are considered: (i) arbitrary polynomial operators with analog delay elements, (ii) limited-degree polynomial operators, excluding delay elements, (iii) sequences of envelope detectors, and (iv) a combination of analog delay elements and linear combiners. For each scenario, the minimum achievable distortion is quantified through derivation of computable expressions in various statistical settings. It is shown that analog processing can significantly reduce the distortion in task reconstruction. Numerical simulations in a Gaussian example are provided to give further insights into the aforementioned analog processing gains.

Design and Analysis of Hardware-limited Non-uniform Task-based Quantizers

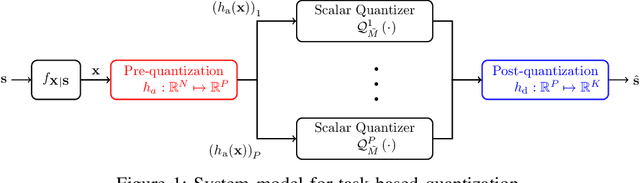
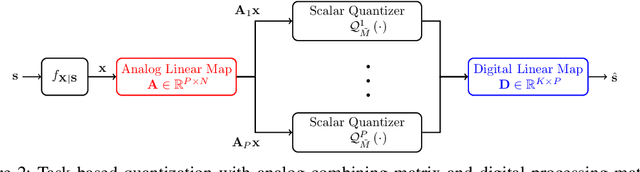
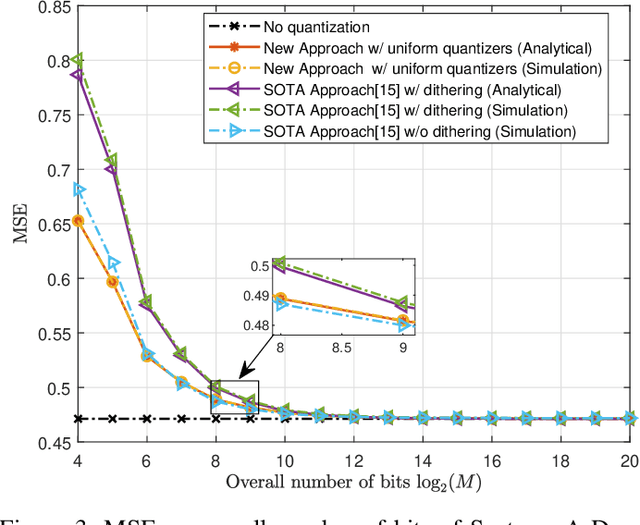
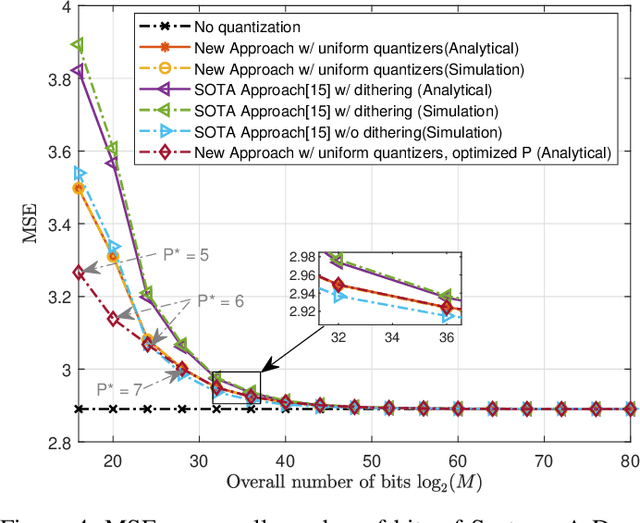
Hardware-limited task-based quantization is a new design paradigm for data acquisition systems equipped with serial scalar analog-to-digital converters using a small number of bits. By taking into account the underlying system task, task-based quantizers can efficiently recover the desired parameters from the low-bit quantized observation. Current design and analysis frameworks for hardware-limited task-based quantization are only applicable to inputs with bounded support and uniform quantizers with non-subtractive dithering. Here, we propose a new framework based on generalized Bussgang decomposition that enables the design and analysis of hardware-limited task-based quantizers that are equipped with non-uniform scalar quantizers or that have inputs with unbounded support. We first consider the scenario in which the task is linear. Under this scenario, we derive new pre-quantization and post-quantization linear mappings for task-based quantizers with mean squared error (MSE) that closely matches the theoretical MSE. Next, we extend the proposed analysis framework to quadratic tasks. We demonstrate that our derived analytical expression for the MSE accurately predicts the performance of task-based quantizers with quadratic tasks.

On the Capacity-Achieving Input of the Gaussian Channel with Polar Quantization

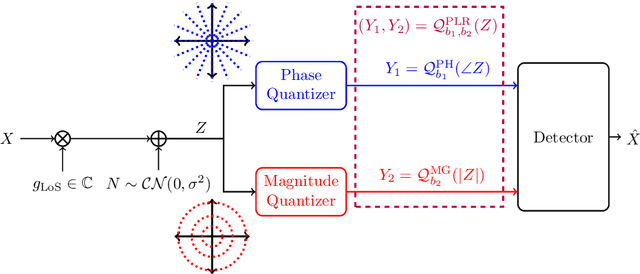
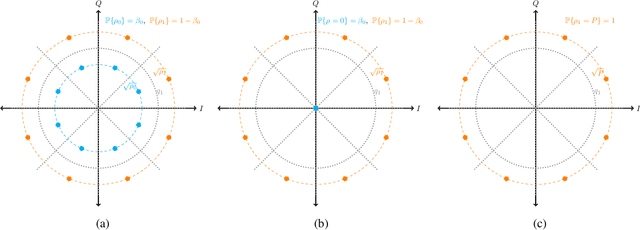
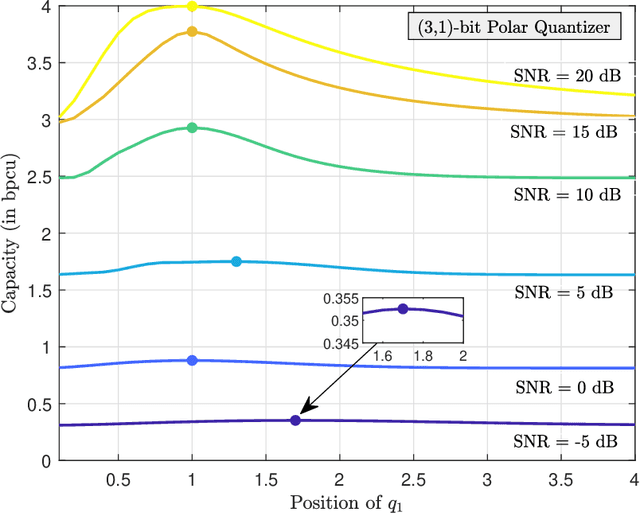
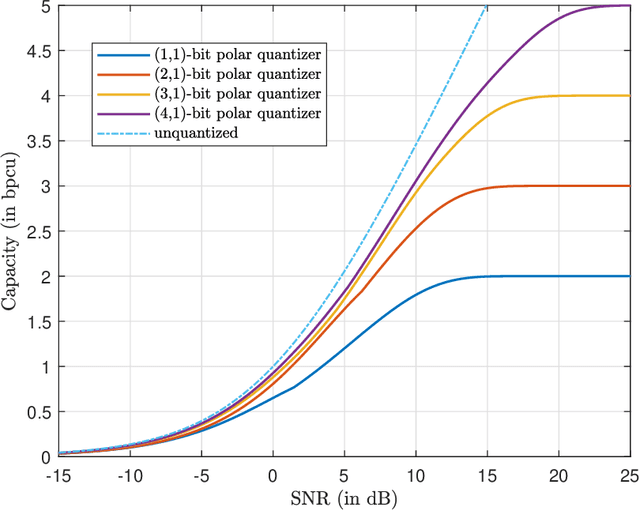
The polar receiver architecture is a receiver design that captures the envelope and phase information of the signal rather than its in-phase and quadrature components. Several studies have demonstrated the robustness of polar receivers to phase noise and other nonlinearities. Yet, the information-theoretic limits of polar receivers with finite-precision quantizers have not been investigated in the literature. The main contribution of this work is to identify the optimal signaling strategy for the additive white Gaussian noise (AWGN) channel with polar quantization at the output. More precisely, we show that the capacity-achieving modulation scheme has an amplitude phase shift keying (APSK) structure. Using this result, the capacity of the AWGN channel with polar quantization at the output is established by numerically optimizing the probability mass function of the amplitude. The capacity of the polar-quantized AWGN channel with $b_1$-bit phase quantizer and optimized single-bit magnitude quantizer is also presented. Our numerical findings suggest the existence of signal-to-noise ratio (SNR) thresholds, above which the number of amplitude levels of the optimal APSK scheme and their respective probabilities change abruptly. Moreover, the manner in which the capacity-achieving input evolves with increasing SNR depends on the number of phase quantization bits.

Capacity Bounds for One-Bit MIMO Gaussian Channels with Analog Combining

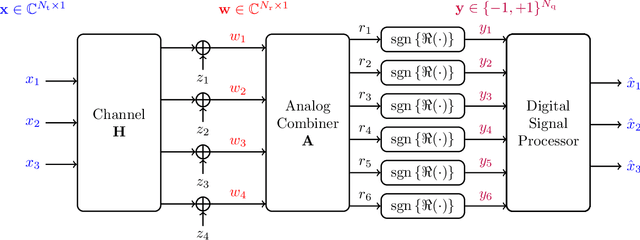
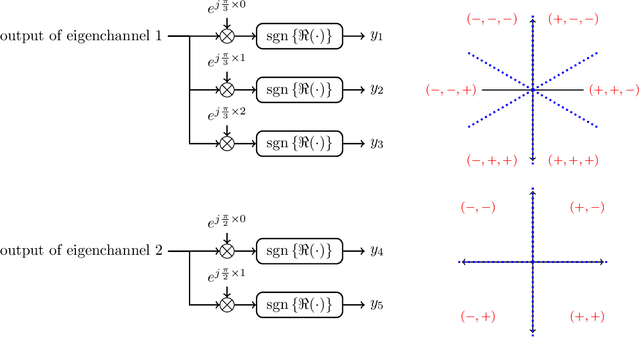
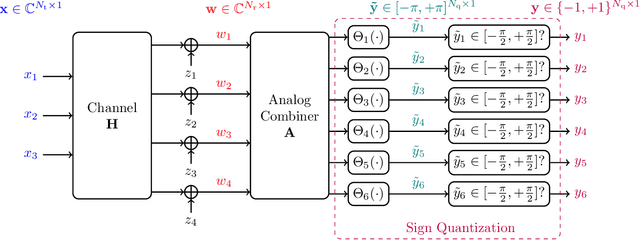
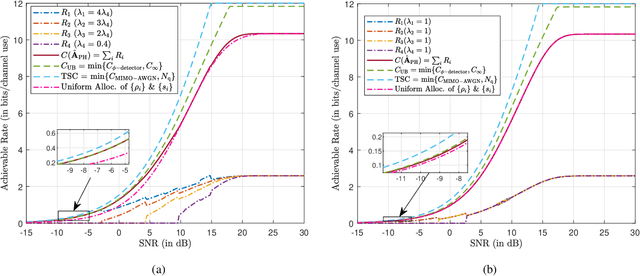
The use of 1-bit analog-to-digital converters (ADCs) is seen as a promising approach to significantly reduce the power consumption and hardware cost of multiple-input multiple-output (MIMO) receivers. However, the nonlinear distortion due to 1-bit quantization fundamentally changes the optimal communication strategy and also imposes a capacity penalty to the system. In this paper, the capacity of a Gaussian MIMO channel in which the antenna outputs are processed by an analog linear combiner and then quantized by a set of zero threshold ADCs is studied. A new capacity upper bound for the zero threshold case is established that is tighter than the bounds available in the literature. In addition, we propose an achievability scheme which configures the analog combiner to create parallel Gaussian channels with phase quantization at the output. Under this class of analog combiners, an algorithm is presented that identifies the analog combiner and input distribution that maximize the achievable rate. Numerical results are provided showing that the rate of the achievability scheme is tight in the low signal-to-noise ratio (SNR) regime. Finally, a new 1-bit MIMO receiver architecture which employs analog temporal and spatial processing is proposed. The proposed receiver attains the capacity in the high SNR regime.

On Minimizing Symbol Error Rate Over Fading Channels with Low-Resolution Quantization

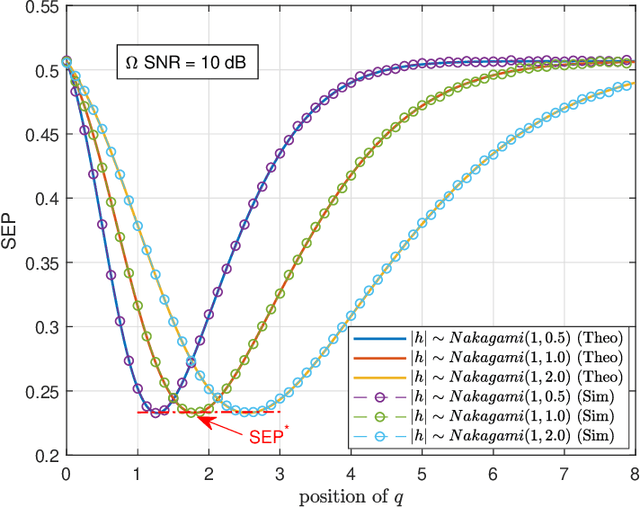
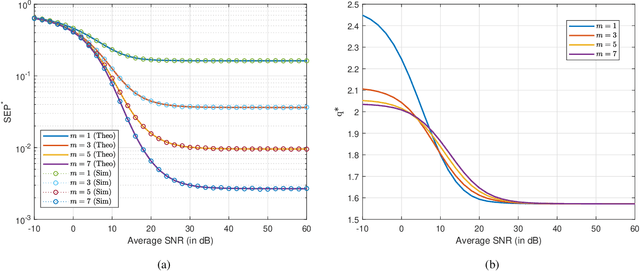
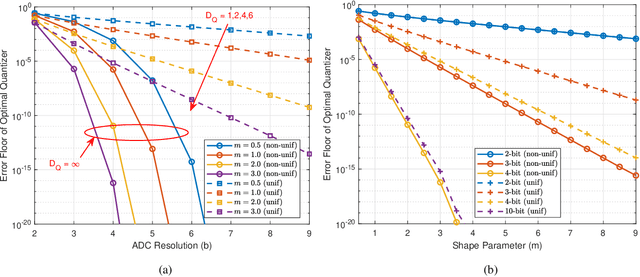
We analyze the symbol error probability (SEP) of $M$-ary pulse amplitude modulation ($M$-PAM) receivers equipped with optimal low-resolution quantizers. We first show that the optimum detector can be reduced to a simple decision rule. Using this simplification, an exact SEP expression for quantized $M$-PAM receivers is obtained when Nakagami-$m$ fading channel is considered. The derived expression enables the optimization of the quantizer and/or constellation under the minimum SEP criterion. Our analysis of optimal quantization for equidistant $M$-PAM receiver reveals the existence of error floor which decays at a double exponential rate with increasing quantization bits, $b$. Moreover, by also allowing the transmitter to optimize the constellation based on the statistics of the fading channel, we prove that the error floor can be eliminated but at a lower decay exponent than the unquantized case. Characterization of this decay exponent is provided in this paper. We also expose the outage performance limitations of SEP-optimal uniform quantizers. To be more precise, its decay exponent does not improve with $b$. Lastly, we demonstrate that the decay exponent of a quantized receiver can be complemented by receive antenna diversity techniques.

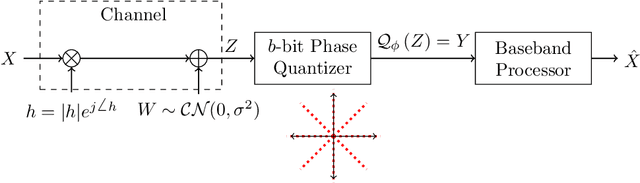
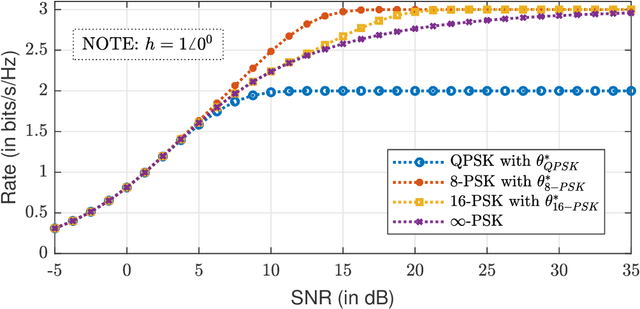
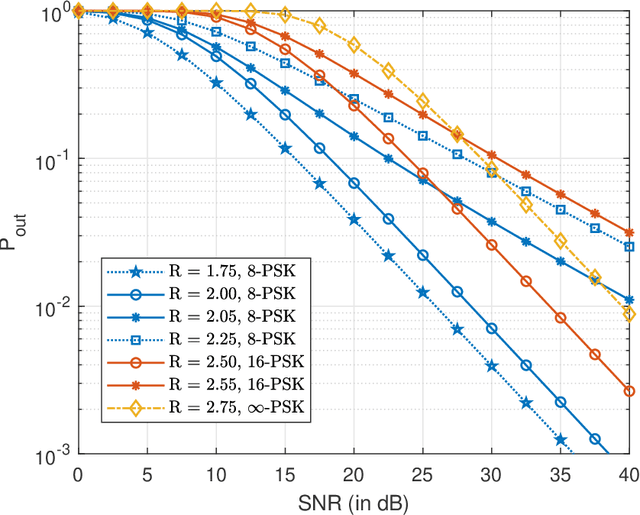
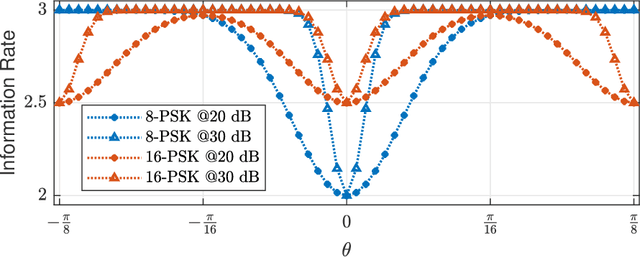
Is Phase Shift Keying Optimal for Channels with Phase-Quantized Output?

This paper establishes the capacity of additive white Gaussian noise (AWGN) channels with phase-quantized output. We show that a rotated $2^b$-phase shift keying scheme is the capacity-achieving input distribution for a complex AWGN channel with $b$-bit phase quantization. The result is then used to establish the expression for the channel capacity as a function of average power constraint $P$ and quantization bits $b$. The outage performance of phase-quantized system is also investigated for the case of Rayleigh fading. Our findings suggest the existence of a threshold in the rate $R$, above which the decay exponent of the outage probability changes abruptly. In fact, this threshold effect in the decay exponent causes $2^b$-PSK to have suboptimal outage performance at high SNR.