A Two-Phase Deep Learning Framework for Adaptive Time-Stepping in High-Speed Flow Modeling

We consider the problem of modeling high-speed flows using machine learning methods. While most prior studies focus on low-speed fluid flows in which uniform time-stepping is practical, flows approaching and exceeding the speed of sound exhibit sudden changes such as shock waves. In such cases, it is essential to use adaptive time-stepping methods to allow a temporal resolution sufficient to resolve these phenomena while simultaneously balancing computational costs. Here, we propose a two-phase machine learning method, known as ShockCast, to model high-speed flows with adaptive time-stepping. In the first phase, we propose to employ a machine learning model to predict the timestep size. In the second phase, the predicted timestep is used as an input along with the current fluid fields to advance the system state by the predicted timestep. We explore several physically-motivated components for timestep prediction and introduce timestep conditioning strategies inspired by neural ODE and Mixture of Experts. As ShockCast is the first framework for learning high-speed flows, we evaluate our methods by generating two supersonic flow datasets, available at https://huggingface.co/datasets/divelab. Our code is publicly available as part of the AIRS library (https://github.com/divelab/AIRS).

Machine Learning Product State Distributions from Initial Reactant States for a Reactive Atom-Diatom Collision System

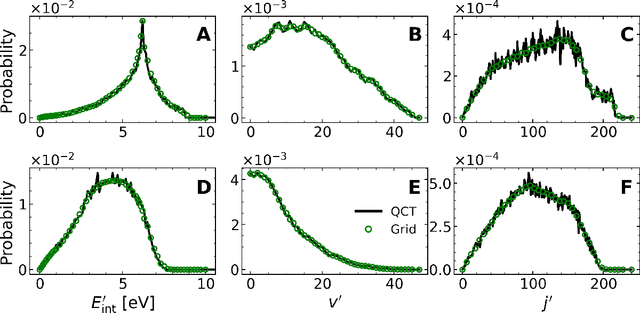
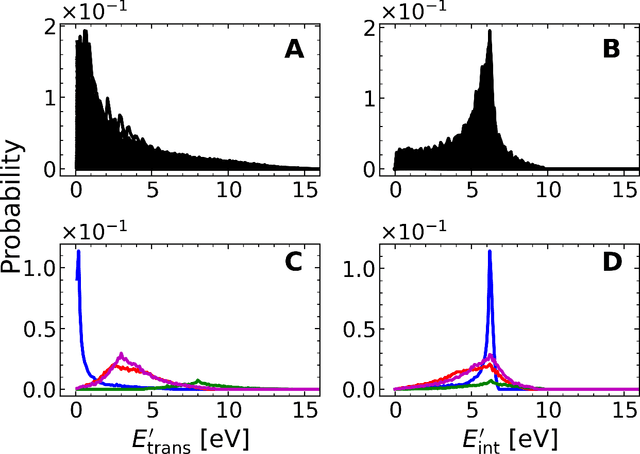
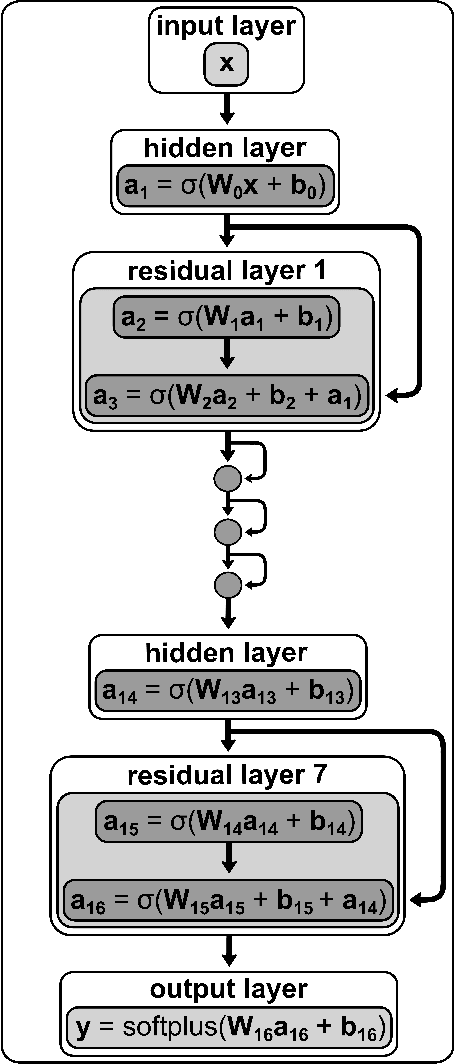
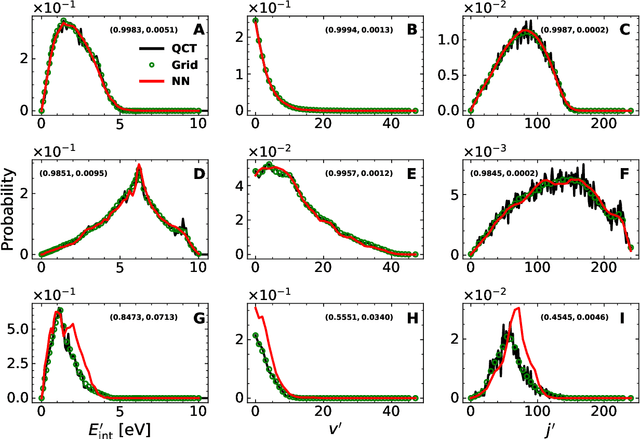
A machine learned (ML) model for predicting product state distributions from specific initial states (state-to-distribution or STD) for reactive atom-diatom collisions is presented and quantitatively tested for the N($^4$S)+O$_{2}$(X$^3 \Sigma_{\rm g}^{-}$) $\rightarrow$ NO(X$^2\Pi$) +O($^3$P) reaction. The reference data set for training the neural network (NN) consists of final state distributions determined from explicit quasi-classical trajectory (QCT) simulations for $\sim 2000$ initial conditions. Overall, the prediction accuracy as quantified by the root-mean-squared difference $(\sim 0.003)$ and the $R^2$ $(\sim 0.99)$ between the reference QCT and predictions of the STD model is high for the test set and off-grid state specific initial conditions and for initial conditions drawn from reactant state distributions characterized by translational, rotational and vibrational temperatures. Compared with a more coarse grained distribution-to-distribution (DTD) model evaluated on the same initial state distributions, the STD model shows comparable performance with the additional benefit of the state resolution in the reactant preparation. Starting from specific initial states also leads to a more diverse range of final state distributions which requires a more expressive neural network to be used compared with DTD. Direct comparison between explicit QCT simulations, the STD model, and the widely used Larsen-Borgnakke (LB) model shows that the STD model is quantitative whereas the LB model is qualitative at best for rotational distributions $P(j')$ and fails for vibrational distributions $P(v')$. As such the STD model can be well-suited for simulating nonequilibrium high-speed flows, e.g., using the direct simulation Monte Carlo method.