FreBIS: Frequency-Based Stratification for Neural Implicit Surface Representations

Neural implicit surface representation techniques are in high demand for advancing technologies in augmented reality/virtual reality, digital twins, autonomous navigation, and many other fields. With their ability to model object surfaces in a scene as a continuous function, such techniques have made remarkable strides recently, especially over classical 3D surface reconstruction methods, such as those that use voxels or point clouds. However, these methods struggle with scenes that have varied and complex surfaces principally because they model any given scene with a single encoder network that is tasked to capture all of low through high-surface frequency information in the scene simultaneously. In this work, we propose a novel, neural implicit surface representation approach called FreBIS to overcome this challenge. FreBIS works by stratifying the scene based on the frequency of surfaces into multiple frequency levels, with each level (or a group of levels) encoded by a dedicated encoder. Moreover, FreBIS encourages these encoders to capture complementary information by promoting mutual dissimilarity of the encoded features via a novel, redundancy-aware weighting module. Empirical evaluations on the challenging BlendedMVS dataset indicate that replacing the standard encoder in an off-the-shelf neural surface reconstruction method with our frequency-stratified encoders yields significant improvements. These enhancements are evident both in the quality of the reconstructed 3D surfaces and in the fidelity of their renderings from any viewpoint.

High-Dimensional Bayesian Optimization with Constraints: Application to Powder Weighing

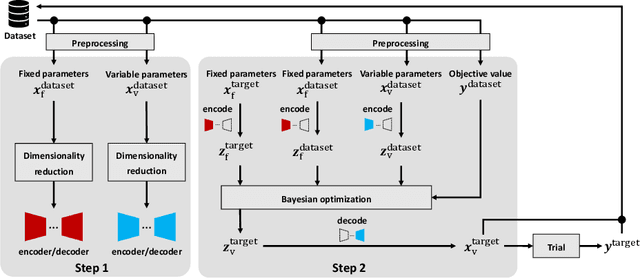
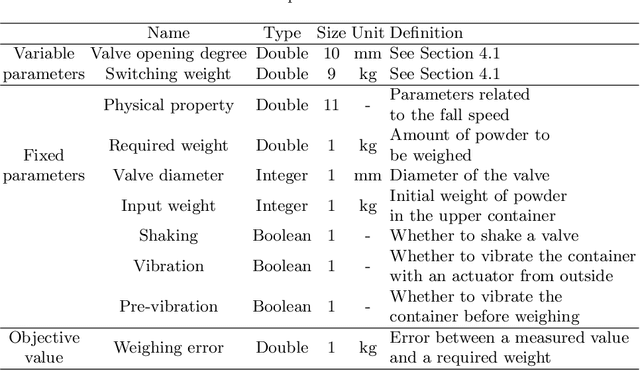
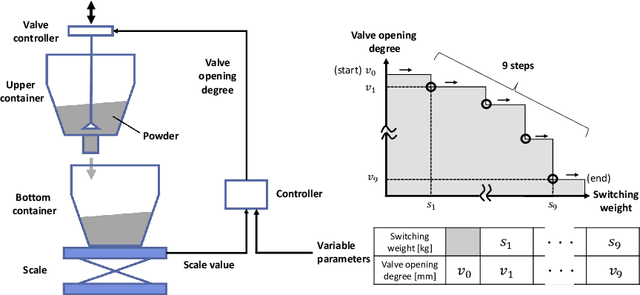
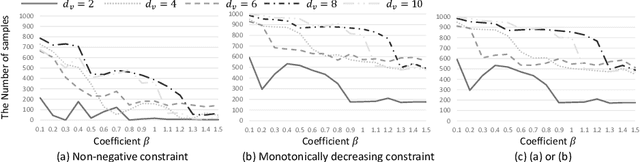
Bayesian optimization works effectively optimizing parameters in black-box problems. However, this method did not work for high-dimensional parameters in limited trials. Parameters can be efficiently explored by nonlinearly embedding them into a low-dimensional space; however, the constraints cannot be considered. We proposed combining parameter decomposition by introducing disentangled representation learning into nonlinear embedding to consider both known equality and unknown inequality constraints in high-dimensional Bayesian optimization. We applied the proposed method to a powder weighing task as a usage scenario. Based on the experimental results, the proposed method considers the constraints and contributes to reducing the number of trials by approximately 66% compared to manual parameter tuning.