Correspondence of high-dimensional emotion structures elicited by video clips between humans and Multimodal LLMs

Recent studies have revealed that human emotions exhibit a high-dimensional, complex structure. A full capturing of this complexity requires new approaches, as conventional models that disregard high dimensionality risk overlooking key nuances of human emotions. Here, we examined the extent to which the latest generation of rapidly evolving Multimodal Large Language Models (MLLMs) capture these high-dimensional, intricate emotion structures, including capabilities and limitations. Specifically, we compared self-reported emotion ratings from participants watching videos with model-generated estimates (e.g., Gemini or GPT). We evaluated performance not only at the individual video level but also from emotion structures that account for inter-video relationships. At the level of simple correlation between emotion structures, our results demonstrated strong similarity between human and model-inferred emotion structures. To further explore whether the similarity between humans and models is at the signle item level or the coarse-categorical level, we applied Gromov Wasserstein Optimal Transport. We found that although performance was not necessarily high at the strict, single-item level, performance across video categories that elicit similar emotions was substantial, indicating that the model could infer human emotional experiences at the category level. Our results suggest that current state-of-the-art MLLMs broadly capture the complex high-dimensional emotion structures at the category level, as well as their apparent limitations in accurately capturing entire structures at the single-item level.

Quantum circuit-like learning: A fast and scalable classical machine-learning algorithm with similar performance to quantum circuit learning

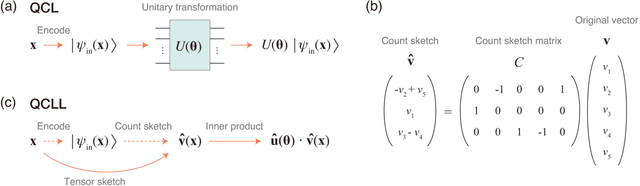
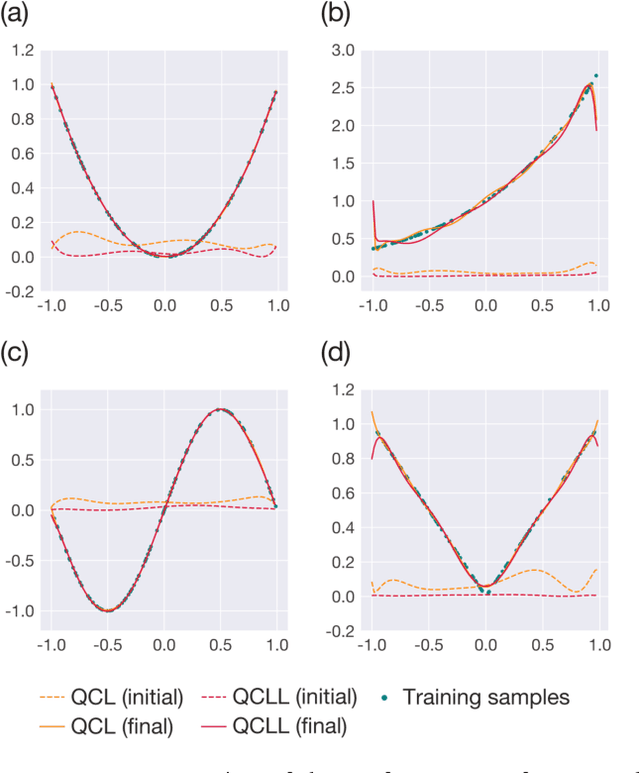
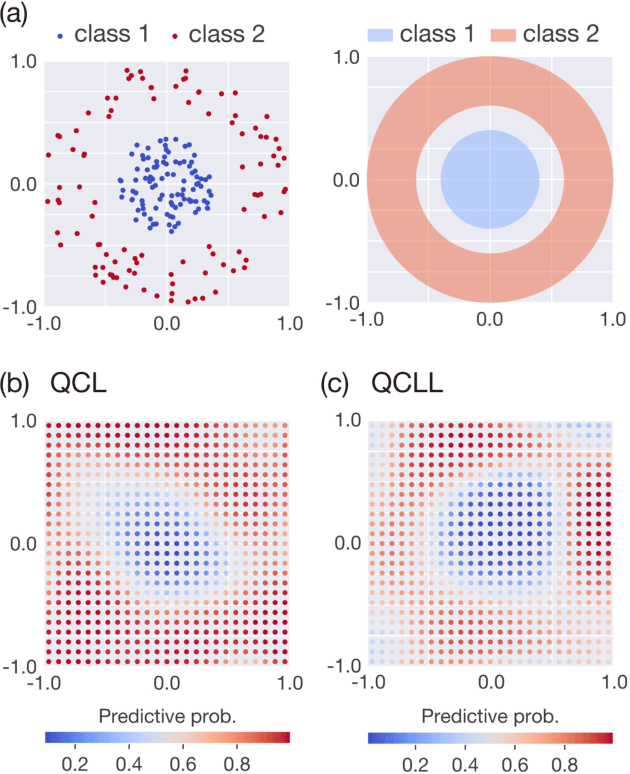
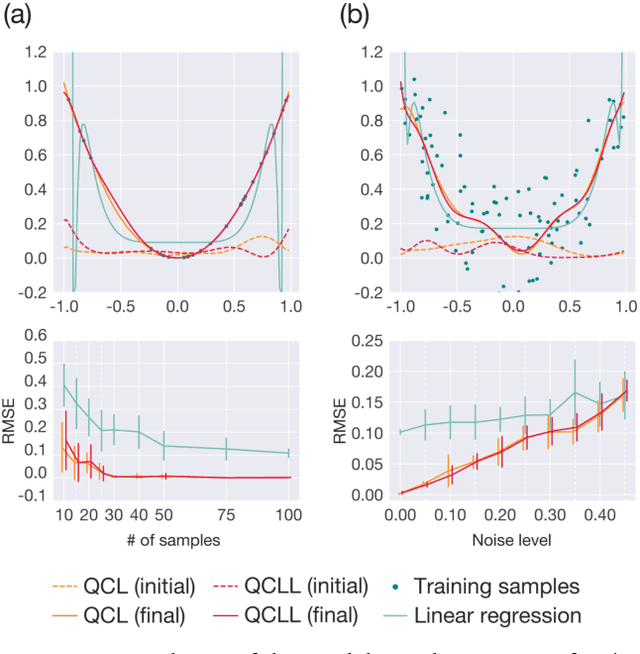
The application of near-term quantum devices to machine learning (ML) has attracted much attention. In one such attempt, Mitarai et al. (2018) proposed a framework to use a quantum circuit for supervised ML tasks, which is called quantum circuit learning (QCL). Due to the use of a quantum circuit, QCL can employ an exponentially high-dimensional Hilbert space as its feature space. However, its efficiency compared to classical algorithms remains unexplored. In this study, using a statistical technique called count sketch, we propose a classical ML algorithm that uses the same Hilbert space. In numerical simulations, our proposed algorithm demonstrates similar performance to QCL for several ML tasks. This provides a new perspective with which to consider the computational and memory efficiency of quantum ML algorithms.

Quantum-inspired canonical correlation analysis for exponentially large dimensional data

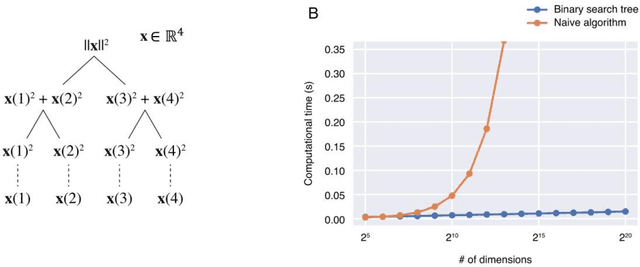
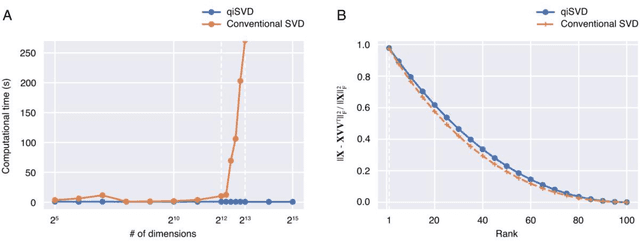
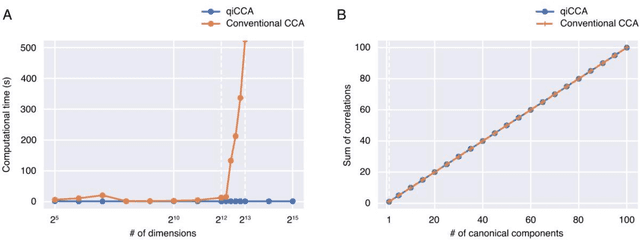
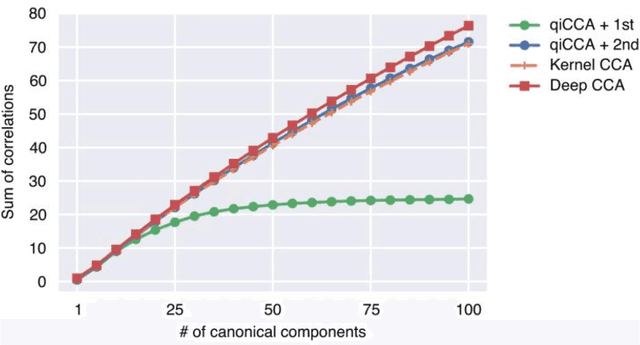
Canonical correlation analysis (CCA) is a technique to find statistical dependencies between a pair of multivariate data. However, its application to high dimensional data is limited due to the resulting time complexity. While the conventional CCA algorithm requires polynomial time, we have developed an algorithm that approximates CCA with computational time proportional to the logarithm of the input dimensionality using quantum-inspired computation. The computational efficiency and approximation performance of the proposed quantum-inspired CCA (qiCCA) algorithm are experimentally demonstrated. Furthermore, the fast computation of qiCCA allows us to directly apply CCA even after nonlinearly mapping raw input data into very high dimensional spaces. Experiments performed using a benchmark dataset demonstrated that, by mapping the raw input data into the high dimensional spaces with second-order monomials, the proposed qiCCA extracted more correlations than linear CCA and was comparable to deep CCA and kernel CCA. These results suggest that qiCCA is considerably useful and quantum-inspired computation has the potential to unlock a new field in which exponentially large dimensional data can be analyzed.