Toward a Robust and Generalizable Metamaterial Foundation Model

Advances in material functionalities drive innovations across various fields, where metamaterials-defined by structure rather than composition-are leading the way. Despite the rise of artificial intelligence (AI)-driven design strategies, their impact is limited by task-specific retraining, poor out-of-distribution(OOD) generalization, and the need for separate models for forward and inverse design. To address these limitations, we introduce the Metamaterial Foundation Model (MetaFO), a Bayesian transformer-based foundation model inspired by large language models. MetaFO learns the underlying mechanics of metamaterials, enabling probabilistic, zero-shot predictions across diverse, unseen combinations of material properties and structural responses. It also excels in nonlinear inverse design, even under OOD conditions. By treating metamaterials as an operator that maps material properties to structural responses, MetaFO uncovers intricate structure-property relationships and significantly expands the design space. This scalable and generalizable framework marks a paradigm shift in AI-driven metamaterial discovery, paving the way for next-generation innovations.

Spectral operator learning for parametric PDEs without data reliance

In this paper, we introduce the Spectral Coefficient Learning via Operator Network (SCLON), a novel operator learning-based approach for solving parametric partial differential equations (PDEs) without the need for data harnessing. The cornerstone of our method is the spectral methodology that employs expansions using orthogonal functions, such as Fourier series and Legendre polynomials, enabling accurate PDE solutions with fewer grid points. By merging the merits of spectral methods - encompassing high accuracy, efficiency, generalization, and the exact fulfillment of boundary conditions - with the prowess of deep neural networks, SCLON offers a transformative strategy. Our approach not only eliminates the need for paired input-output training data, which typically requires extensive numerical computations, but also effectively learns and predicts solutions of complex parametric PDEs, ranging from singularly perturbed convection-diffusion equations to the Navier-Stokes equations. The proposed framework demonstrates superior performance compared to existing scientific machine learning techniques, offering solutions for multiple instances of parametric PDEs without harnessing data. The mathematical framework is robust and reliable, with a well-developed loss function derived from the weak formulation, ensuring accurate approximation of solutions while exactly satisfying boundary conditions. The method's efficacy is further illustrated through its ability to accurately predict intricate natural behaviors like the Kolmogorov flow and boundary layers. In essence, our work pioneers a compelling avenue for parametric PDE solutions, serving as a bridge between traditional numerical methodologies and cutting-edge machine learning techniques in the realm of scientific computation.

Unsupervised Legendre-Galerkin Neural Network for Stiff Partial Differential Equations

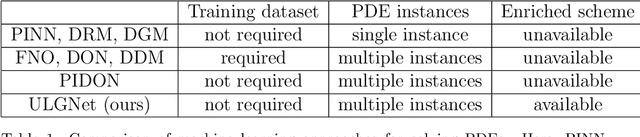
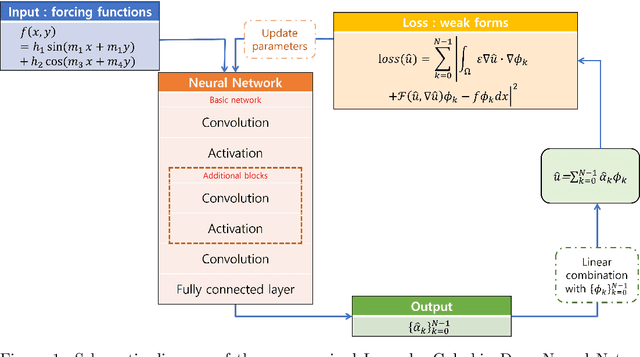
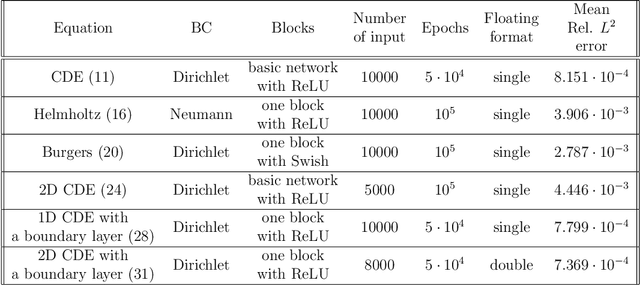
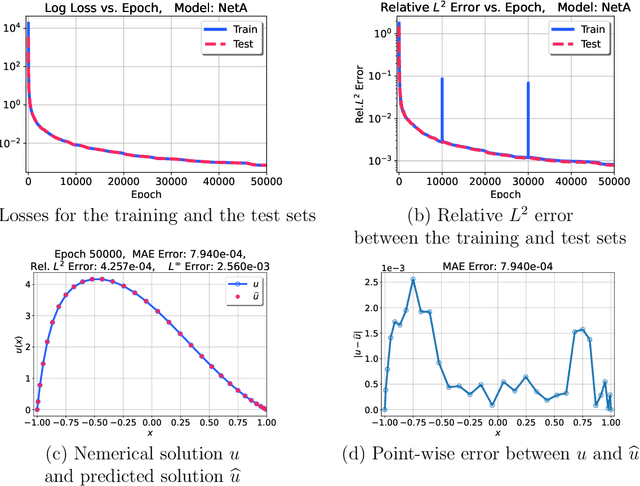
Machine learning methods have been lately used to solve differential equations and dynamical systems. These approaches have been developed into a novel research field known as scientific machine learning in which techniques such as deep neural networks and statistical learning are applied to classical problems of applied mathematics. Because neural networks provide an approximation capability, computational parameterization through machine learning and optimization methods achieve noticeable performance when solving various partial differential equations (PDEs). In this paper, we develop a novel numerical algorithm that incorporates machine learning and artificial intelligence to solve PDEs. In particular, we propose an unsupervised machine learning algorithm based on the Legendre-Galerkin neural network to find an accurate approximation to the solution of different types of PDEs. The proposed neural network is applied to the general 1D and 2D PDEs as well as singularly perturbed PDEs that possess boundary layer behavior.