Phase-Pole-Free Images and Smooth Coil Sensitivity Maps by Regularized Nonlinear Inversion

Purpose: Phase singularities are a common problem in image reconstruction with auto-calibrated sensitivities due to an inherent ambiguity of the estimation problem. The purpose of this work is to develop a method for detecting and correcting phase poles in non-linear inverse (NLINV) reconstruction of MR images and coil sensitivity maps. Methods: Phase poles are detected in individual coil sensitivity maps by computing the curl in each pixel. A weighted average of the curl in each coil is computed to detect phase poles. Phase pole detection and correction is then integrated into the iteratively regularized Gauss-Newton method of the NLINV algorithm, which then avoid phase singularities in the reconstructed images. The method is evaluated for reconstruction of accelerated Cartesian MPRAGE data of the brain and interactive radial real-time MRI of the human heart. Results: Phase poles are reliably removed in NLINV reconstructions for both applications. NLINV with phase pole correction can reliably and efficiently estimate coil sensitivity profiles free from singularities even from very small ($7\times7$) auto-calibration (AC) regions. Conclusion: NLINV emerges as an efficient and reliable tool for image reconstruction and coil sensitivity estimation in challenging MRI applications.

Self Supervised Learning for Improved Calibrationless Radial MRI with NLINV-Net

Purpose: To develop a neural network architecture for improved calibrationless reconstruction of radial data when no ground truth is available for training. Methods: NLINV-Net is a model-based neural network architecture that directly estimates images and coil sensitivities from (radial) k-space data via non-linear inversion (NLINV). Combined with a training strategy using self-supervision via data undersampling (SSDU), it can be used for imaging problems where no ground truth reconstructions are available. We validated the method for (1) real-time cardiac imaging and (2) single-shot subspace-based quantitative T1 mapping. Furthermore, region-optimized virtual (ROVir) coils were used to suppress artifacts stemming from outside the FoV and to focus the k-space based SSDU loss on the region of interest. NLINV-Net based reconstructions were compared with conventional NLINV and PI-CS (parallel imaging + compressed sensing) reconstruction and the effect of the region-optimized virtual coils and the type of training loss was evaluated qualitatively. Results: NLINV-Net based reconstructions contain significantly less noise than the NLINV-based counterpart. ROVir coils effectively suppress streakings which are not suppressed by the neural networks while the ROVir-based focussed loss leads to visually sharper time series for the movement of the myocardial wall in cardiac real-time imaging. For quantitative imaging, T1-maps reconstructed using NLINV-Net show similar quality as PI-CS reconstructions, but NLINV-Net does not require slice-specific tuning of the regularization parameter. Conclusion: NLINV-Net is a versatile tool for calibrationless imaging which can be used in challenging imaging scenarios where a ground truth is not available.

Deep, Deep Learning with BART

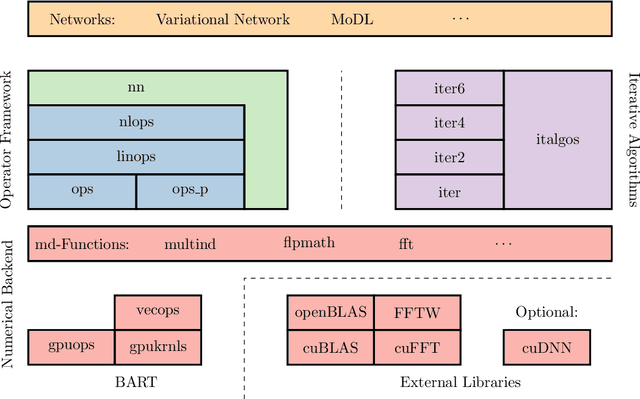
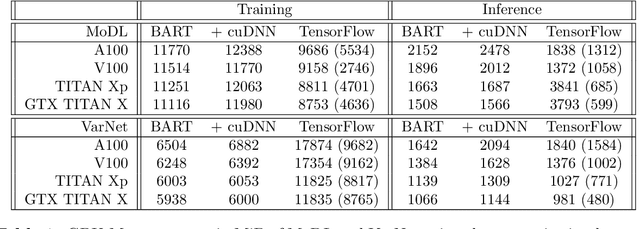
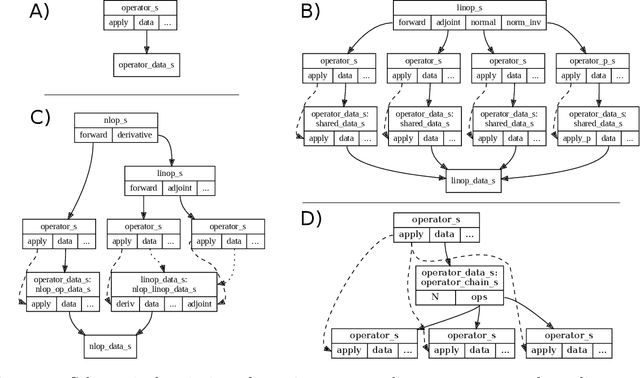
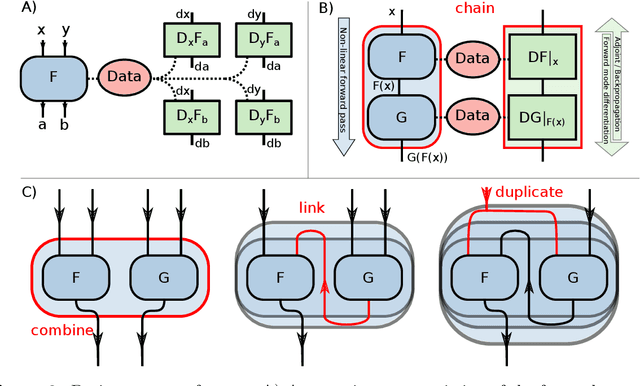
Purpose: To develop a deep-learning-based image reconstruction framework for reproducible research in MRI. Methods: The BART toolbox offers a rich set of implementations of calibration and reconstruction algorithms for parallel imaging and compressed sensing. In this work, BART was extended by a non-linear operator framework that provides automatic differentiation to allow computation of gradients. Existing MRI-specific operators of BART, such as the non-uniform fast Fourier transform, are directly integrated into this framework and are complemented by common building blocks used in neural networks. To evaluate the use of the framework for advanced deep-learning-based reconstruction, two state-of-the-art unrolled reconstruction networks, namely the Variational Network [1] and MoDL [2], were implemented. Results: State-of-the-art deep image-reconstruction networks can be constructed and trained using BART's gradient based optimization algorithms. The BART implementation achieves a similar performance in terms of training time and reconstruction quality compared to the original implementations based on TensorFlow. Conclusion: By integrating non-linear operators and neural networks into BART, we provide a general framework for deep-learning-based reconstruction in MRI.

Free-Breathing Water, Fat, $R_2^{\star}$ and $B_0$ Field Mapping of the Liver Using Multi-Echo Radial FLASH and Regularized Model-based Reconstruction

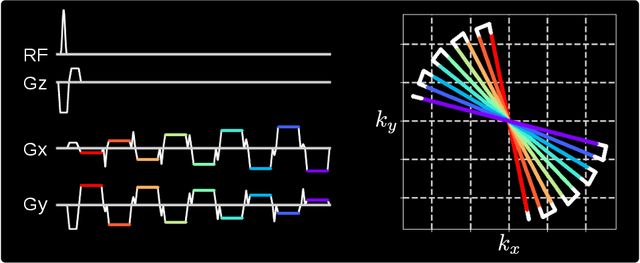
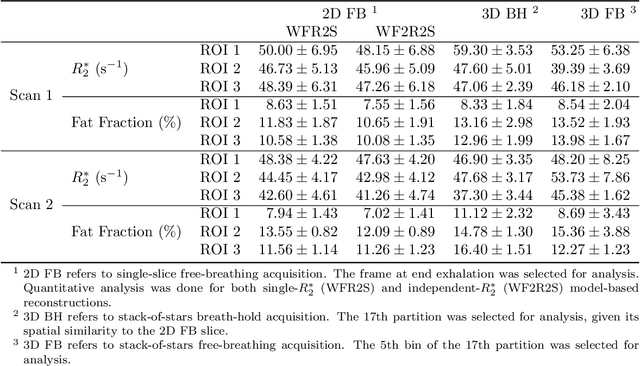
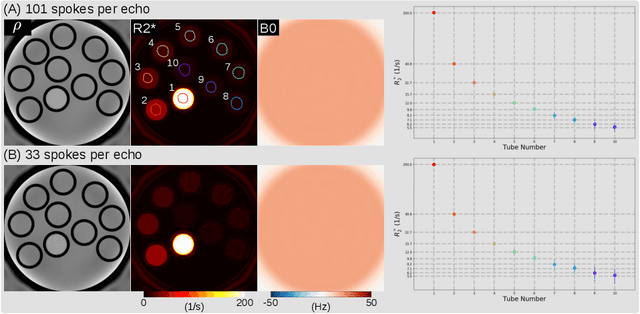
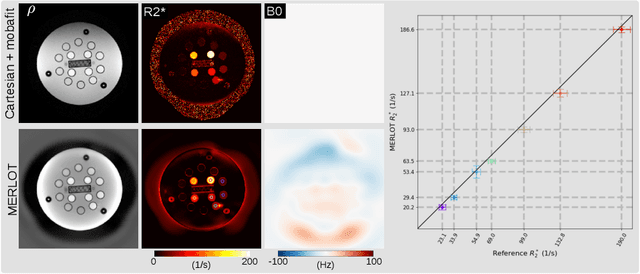
Purpose: To achieve free-breathing quantitative fat and $R_2^{\star}$ mapping of the liver using a generalized model-based iterative reconstruction, dubbed as MERLOT. Methods: For acquisition, we use a multi-echo radial FLASH sequence that acquires multiple echoes with different complementary radial spoke encodings. We investigate real-time single-slice and volumetric multi-echo radial FLASH acquisition. For the latter, the sampling scheme is extended to a volumetric stack-of-stars acquisition. Model-based reconstruction based on generalized nonlinear inversion is used to jointly estimate water, fat, $R_2^{\star}$, $B_0$ field inhomogeneity, and coil sensitivity maps from the multi-coil multi-echo radial spokes. Spatial smoothness regularization is applied onto the B 0 field and coil sensitivity maps, whereas joint sparsity regularization is employed for the other parameter maps. The method integrates calibration-less parallel imaging and compressed sensing and was implemented in BART. For the volumetric acquisition, the respiratory motion is resolved with self-gating using SSA-FARY. The quantitative accuracy of the proposed method was validated via numerical simulation, the NIST phantom, a water/fat phantom, and in in-vivo liver studies. Results: For real-time acquisition, the proposed model-based reconstruction allowed acquisition of dynamic liver fat fraction and $R_2^{\star}$ maps at a temporal resolution of 0.3 s per frame. For the volumetric acquisition, whole liver coverage could be achieved in under 2 minutes using the self-gated motion-resolved reconstruction. Conclusion: The proposed multi-echo radial sampling sequence achieves fast k -space coverage and is robust to motion. The proposed model-based reconstruction yields spatially and temporally resolved liver fat fraction, $R_2^{\star}$ and $B_0$ field maps at high undersampling factor and with volume coverage.