The Randomized Elliptical Potential Lemma with an Application to Linear Thompson Sampling

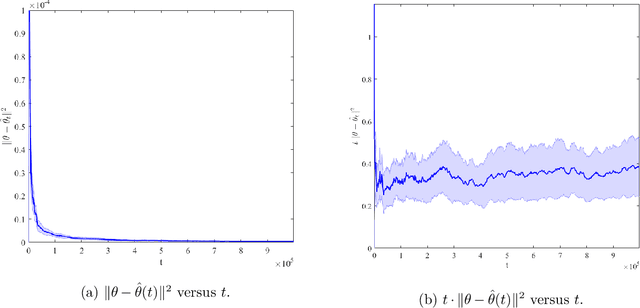
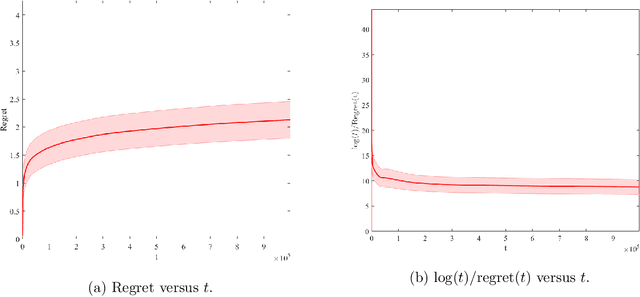
In this note, we introduce a randomized version of the well-known elliptical potential lemma that is widely used in the analysis of algorithms in sequential learning and decision-making problems such as stochastic linear bandits. Our randomized elliptical potential lemma relaxes the Gaussian assumption on the observation noise and on the prior distribution of the problem parameters. We then use this generalization to prove an improved Bayesian regret bound for Thompson sampling for the linear stochastic bandits with changing action sets where prior and noise distributions are general. This bound is minimax optimal up to constants.

On Worst-case Regret of Linear Thompson Sampling

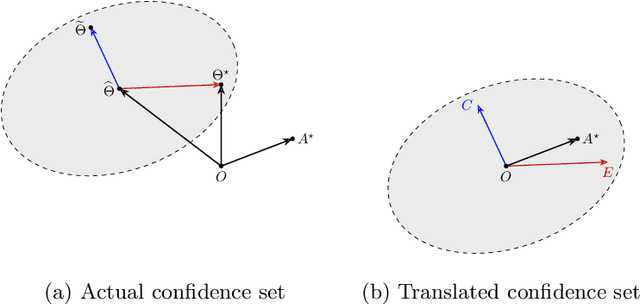
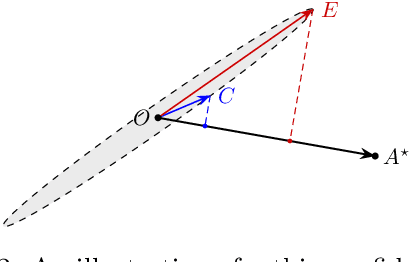
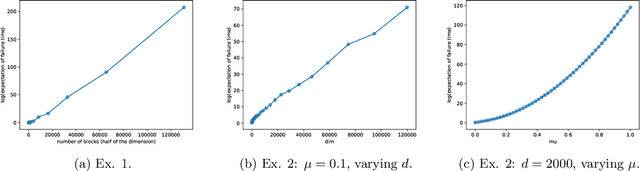
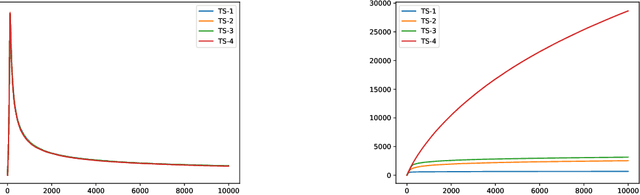
In this paper, we consider the worst-case regret of Linear Thompson Sampling (LinTS) for the linear bandit problem. Russo and Van Roy (2014) show that the Bayesian regret of LinTS is bounded above by $\widetilde{\mathcal{O}}(d\sqrt{T})$ where $T$ is the time horizon and $d$ is the number of parameters. While this bound matches the minimax lower-bounds for this problem up to logarithmic factors, the existence of a similar worst-case regret bound is still unknown. The only known worst-case regret bound for LinTS, due to Agrawal and Goyal (2013b); Abeille et al. (2017), is $\widetilde{\mathcal{O}}(d\sqrt{dT})$ which requires the posterior variance to be inflated by a factor of $\widetilde{\mathcal{O}}(\sqrt{d})$. While this bound is far from the minimax optimal rate by a factor of $\sqrt{d}$, in this paper we show that it is the best possible one can get, settling an open problem stated in Russo et al. (2018). Specifically, we construct examples to show that, without the inflation, LinTS can incur linear regret up to time $\exp(\mathcal{O}(d))$. We then demonstrate that, under mild conditions, a slightly modified version of LinTS requires only an $\widetilde{\mathcal{O}}(1)$ inflation where the constant depends on the diversity of the optimal arm.

Optimal and Greedy Algorithms for Multi-Armed Bandits with Many Arms

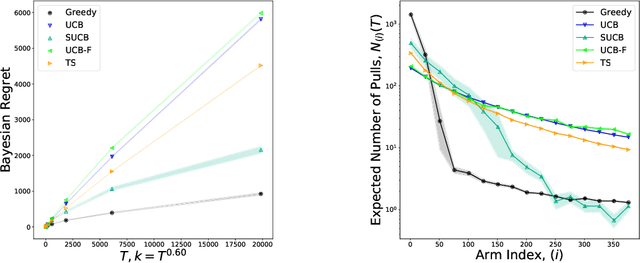
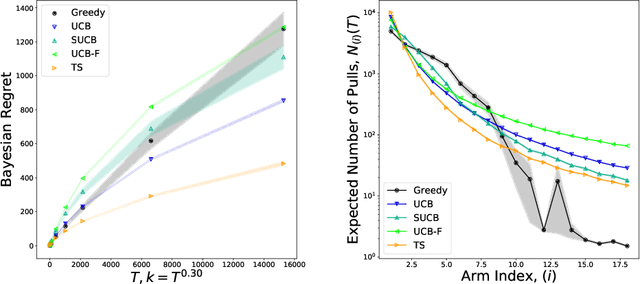
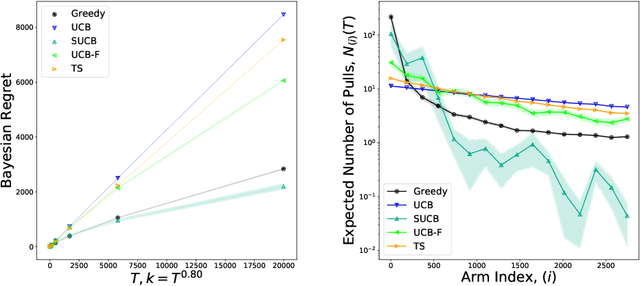
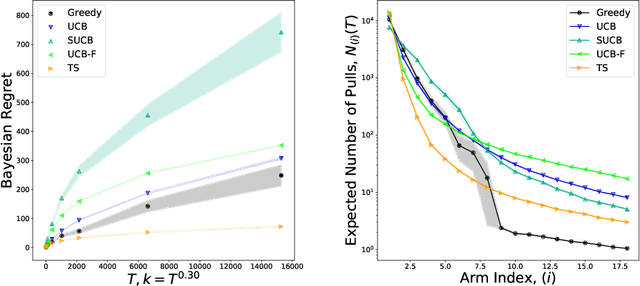
We characterize Bayesian regret in a stochastic multi-armed bandit problem with a large but finite number of arms. In particular, we assume the number of arms $k$ is $T^{\alpha}$, where $T$ is the time-horizon and $\alpha$ is in $(0,1)$. We consider a Bayesian setting where the reward distribution of each arm is drawn independently from a common prior, and provide a complete analysis of expected regret with respect to this prior. Our results exhibit a sharp distinction around $\alpha = 1/2$. When $\alpha < 1/2$, the fundamental lower bound on regret is $\Omega(k)$; and it is achieved by a standard UCB algorithm. When $\alpha > 1/2$, the fundamental lower bound on regret is $\Omega(\sqrt{T})$, and it is achieved by an algorithm that first subsamples $\sqrt{T}$ arms uniformly at random, then runs UCB on just this subset. Interestingly, we also find that a sufficiently large number of arms allows the decision-maker to benefit from "free" exploration if she simply uses a greedy algorithm. In particular, this greedy algorithm exhibits a regret of $\tilde{O}(\max(k,T/\sqrt{k}))$, which translates to a {\em sublinear} (though not optimal) regret in the time horizon. We show empirically that this is because the greedy algorithm rapidly disposes of underperforming arms, a beneficial trait in the many-armed regime. Technically, our analysis of the greedy algorithm involves a novel application of the Lundberg inequality, an upper bound for the ruin probability of a random walk; this approach may be of independent interest.

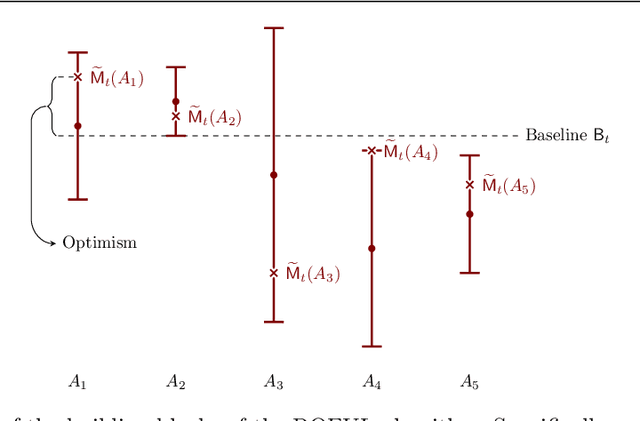
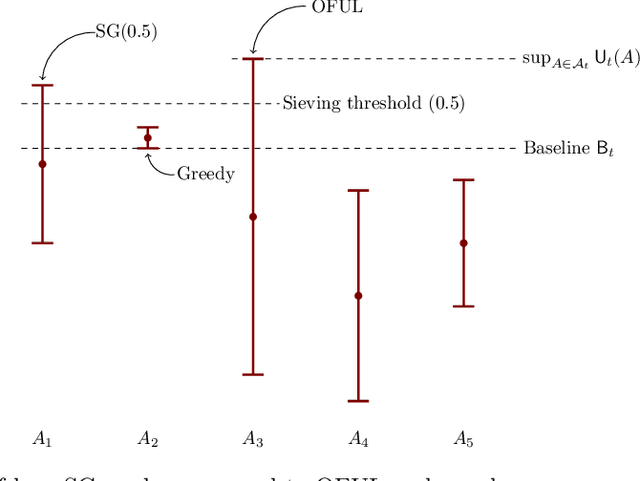
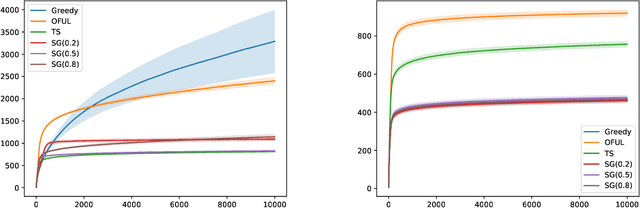
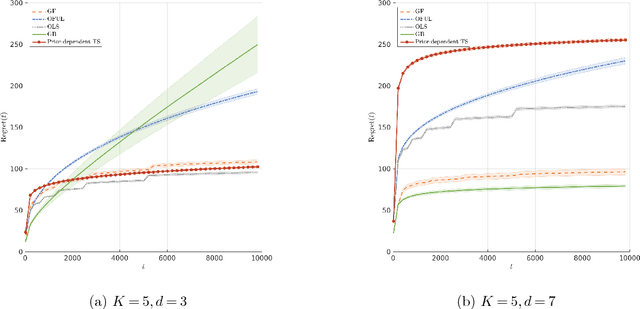
A General Framework to Analyze Stochastic Linear Bandit

In this paper we study the well-known stochastic linear bandit problem where a decision-maker sequentially chooses among a set of given actions in R^d, observes their noisy reward, and aims to maximize her cumulative expected reward over a horizon of length T. We introduce a general family of algorithms for the problem and prove that they are rate optimal. We also show that several well-known algorithms for the problem such as optimism in the face of uncertainty linear bandit (OFUL) and Thompson sampling (TS) are special cases of our family of algorithms. Therefore, we obtain a unified proof of rate optimality for both of these algorithms. Our results include both adversarial action sets (when actions are potentially selected by an adversary) and stochastic action sets (when actions are independently drawn from an unknown distribution). In terms of regret, our results apply to both Bayesian and worst-case regret settings. Our new unified analysis technique also yields a number of new results and solves two open problems known in the literature. Most notably, (1) we show that TS can incur a linear worst-case regret, unless it uses inflated (by a factor of $\sqrt{d}$) posterior variances at each step. This shows that the best known worst-case regret bound for TS, that is given by (Agrawal & Goyal, 2013; Abeille et al., 2017) and is worse (by a factor of \sqrt(d)) than the best known Bayesian regret bound given by Russo and Van Roy (2014) for TS, is tight. This settles an open problem stated in Russo et al., 2018. (2) Our proof also shows that TS can incur a linear Bayesian regret if it does not use the correct prior or noise distribution. (3) Under a generalized gap assumption and a margin condition, as in Goldenshluger & Zeevi, 2013, we obtain a poly-logarithmic (in $T$) regret bound for OFUL and TS in the stochastic setting.

Optimal Experimental Design for Staggered Rollouts

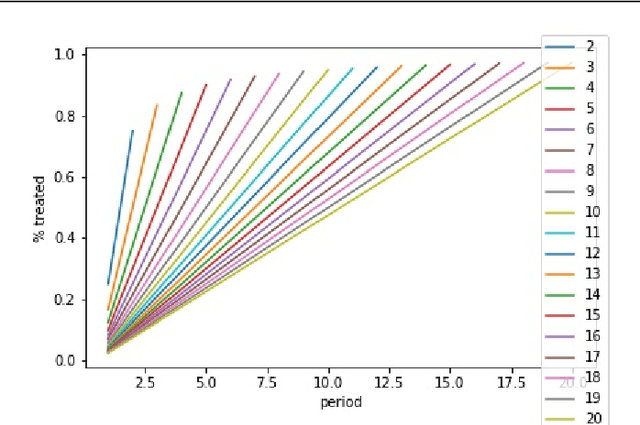
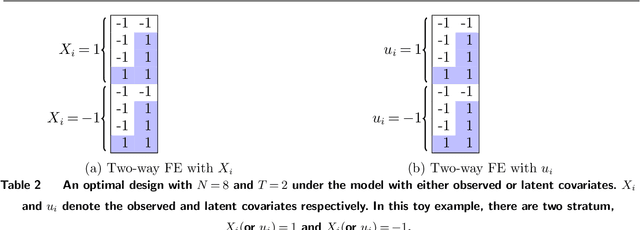
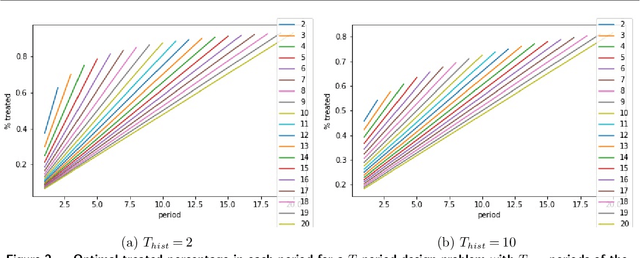
Experimentation has become an increasingly prevalent tool for guiding policy choices, firm decisions, and product innovation. A common hurdle in designing experiments is the lack of statistical power. In this paper, we study optimal multi-period experimental design under the constraint that the treatment cannot be easily removed once implemented; for example, a government or firm might implement treatment in different geographies at different times, where the treatment cannot be easily removed due to practical constraints. The design problem is to select which units to treat at which time, intending to test hypotheses about the effect of the treatment. When the potential outcome is a linear function of a unit effect, a time effect, and observed discrete covariates, we provide an analytically feasible solution to the design problem where the variance of the estimator for the treatment effect is at most 1+O(1/N^2) times the variance of the optimal design, where N is the number of units. This solution assigns units in a staggered treatment adoption pattern, where the proportion treated is a linear function of time. In the general setting where outcomes depend on latent covariates, we show that historical data can be utilized in the optimal design. We propose a data-driven local search algorithm with the minimax decision criterion to assign units to treatment times. We demonstrate that our approach improves upon benchmark experimental designs through synthetic experiments on real-world data sets from several domains, including healthcare, finance, and retail. Finally, we consider the case where the treatment effect changes with the time of treatment, showing that the optimal design treats a smaller fraction of units at the beginning and a greater share at the end.

On Low-rank Trace Regression under General Sampling Distribution

A growing number of modern statistical learning problems involve estimating a large number of parameters from a (smaller) number of observations. In a subset of these problems (matrix completion, matrix compressed sensing, and multi-task learning) the unknown parameters form a high-dimensional matrix, and two popular approaches for the estimation are trace-norm regularized linear regression or alternating minimization. It is also known that these estimators satisfy certain optimal tail bounds under assumptions on rank, coherence, or spikiness of the unknown matrix. We study a general family of estimators and sampling distribution that include the above two estimators, and introduce a general notion of spikiness and rank for the unknown matrix. Next, we extend the existing literature on the analysis of these estimators and provide a unifying technique to prove tail bounds for the estimation error. We demonstrate the benefit of this generalization by studying its application to four problems of (1) matrix completion, (2) multi-task learning, (3) compressed sensing with Gaussian ensembles, and (4) compressed sensing with factored measurements. For (1) and (3), we recover matching tail bounds as those found in the literature, and for (2) and (4) we obtain (to the best of our knowledge) the first tail bounds. Our approach relies on a generic recipe to prove restricted strong convexity for the sampling operator of the trace regression, that only requires finding upper bounds on certain norms of the parameter matrix.

Mostly Exploration-Free Algorithms for Contextual Bandits

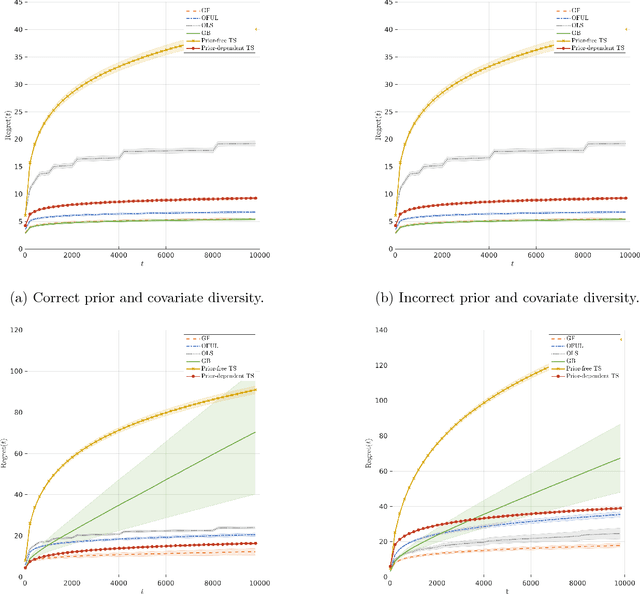
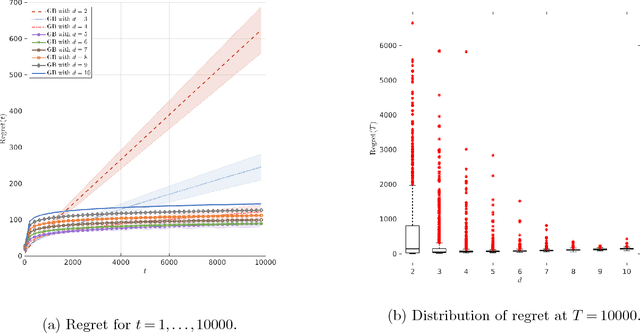
The contextual bandit literature has traditionally focused on algorithms that address the exploration-exploitation tradeoff. In particular, greedy algorithms that exploit current estimates without any exploration may be sub-optimal in general. However, exploration-free greedy algorithms are desirable in practical settings where exploration may be costly or unethical (e.g., clinical trials). Surprisingly, we find that a simple greedy algorithm can be rate-optimal (achieves asymptotically optimal regret) if there is sufficient randomness in the observed contexts (covariates). We prove that this is always the case for a two-armed bandit under a general class of context distributions that satisfy a condition we term $\textit{covariate diversity}$. Furthermore, even absent this condition, we show that a greedy algorithm can be rate optimal with positive probability. Thus, standard bandit algorithms may unnecessarily explore. Motivated by these results, we introduce Greedy-First, a new algorithm that uses only observed contexts and rewards to determine whether to follow a greedy algorithm or to explore. We prove that this algorithm is rate-optimal without any additional assumptions on the context distribution or the number of arms. Extensive simulations demonstrate that Greedy-First successfully reduces exploration and outperforms existing (exploration-based) contextual bandit algorithms such as Thompson sampling or upper confidence bound (UCB).

Scalable Approximations for Generalized Linear Problems

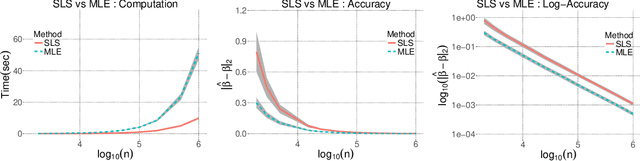
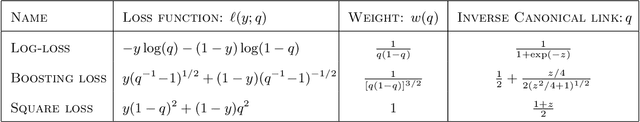
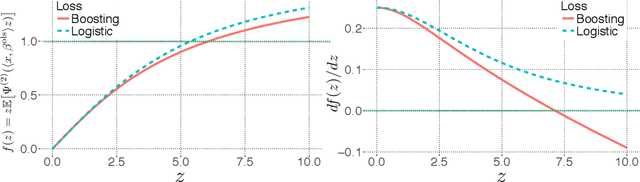
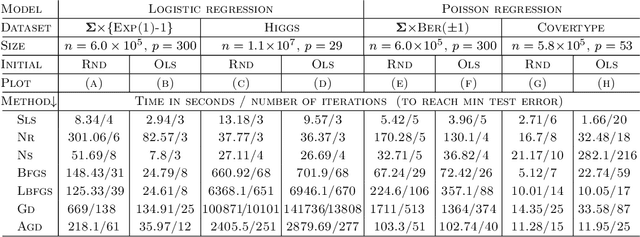
In stochastic optimization, the population risk is generally approximated by the empirical risk. However, in the large-scale setting, minimization of the empirical risk may be computationally restrictive. In this paper, we design an efficient algorithm to approximate the population risk minimizer in generalized linear problems such as binary classification with surrogate losses and generalized linear regression models. We focus on large-scale problems, where the iterative minimization of the empirical risk is computationally intractable, i.e., the number of observations $n$ is much larger than the dimension of the parameter $p$, i.e. $n \gg p \gg 1$. We show that under random sub-Gaussian design, the true minimizer of the population risk is approximately proportional to the corresponding ordinary least squares (OLS) estimator. Using this relation, we design an algorithm that achieves the same accuracy as the empirical risk minimizer through iterations that attain up to a cubic convergence rate, and that are cheaper than any batch optimization algorithm by at least a factor of $\mathcal{O}(p)$. We provide theoretical guarantees for our algorithm, and analyze the convergence behavior in terms of data dimensions. Finally, we demonstrate the performance of our algorithm on well-known classification and regression problems, through extensive numerical studies on large-scale datasets, and show that it achieves the highest performance compared to several other widely used and specialized optimization algorithms.

Dynamic Pricing with Demand Covariates

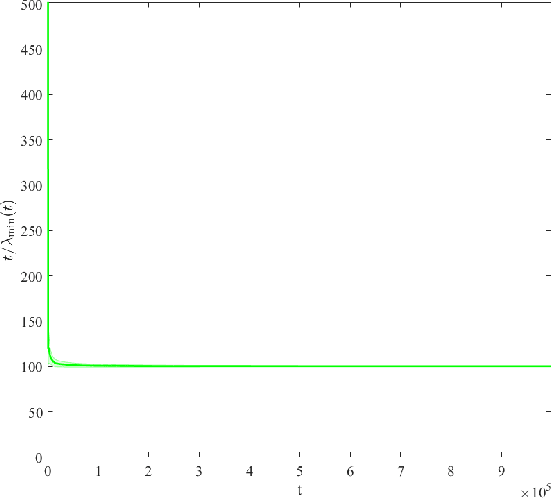
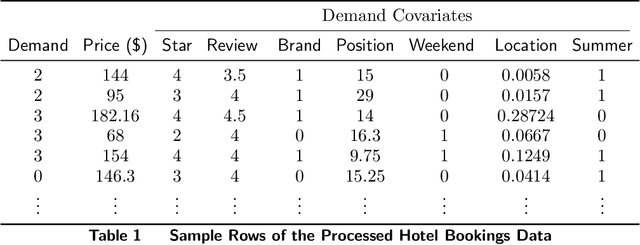
We consider a firm that sells products over $T$ periods without knowing the demand function. The firm sequentially sets prices to earn revenue and to learn the underlying demand function simultaneously. A natural heuristic for this problem, commonly used in practice, is greedy iterative least squares (GILS). At each time period, GILS estimates the demand as a linear function of the price by applying least squares to the set of prior prices and realized demands. Then a price that maximizes the revenue, given the estimated demand function, is used for the next time period. The performance is measured by the regret, which is the expected revenue loss from the optimal (oracle) pricing policy when the demand function is known. Recently, den Boer and Zwart (2014) and Keskin and Zeevi (2014) demonstrated that GILS is sub-optimal. They introduced algorithms which integrate forced price dispersion with GILS and achieve asymptotically optimal performance. In this paper, we consider this dynamic pricing problem in a data-rich environment. In particular, we assume that the firm knows the expected demand under a particular price from historical data, and in each period, before setting the price, the firm has access to extra information (demand covariates) which may be predictive of the demand. We prove that in this setting GILS achieves asymptotically optimal regret of order $\log(T)$. We also show the following surprising result: in the original dynamic pricing problem of den Boer and Zwart (2014) and Keskin and Zeevi (2014), inclusion of any set of covariates in GILS as potential demand covariates (even though they could carry no information) would make GILS asymptotically optimal. We validate our results via extensive numerical simulations on synthetic and real data sets.

Belief-Propagation for Weighted b-Matchings on Arbitrary Graphs and its Relation to Linear Programs with Integer Solutions

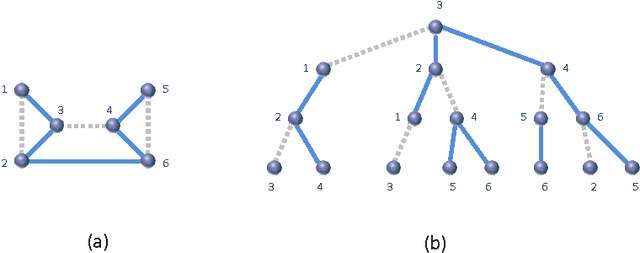
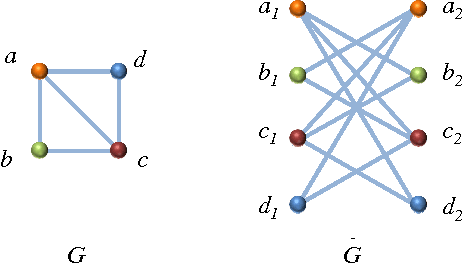
We consider the general problem of finding the minimum weight $\bm$-matching on arbitrary graphs. We prove that, whenever the linear programming (LP) relaxation of the problem has no fractional solutions, then the belief propagation (BP) algorithm converges to the correct solution. We also show that when the LP relaxation has a fractional solution then the BP algorithm can be used to solve the LP relaxation. Our proof is based on the notion of graph covers and extends the analysis of (Bayati-Shah-Sharma 2005 and Huang-Jebara 2007}. These results are notable in the following regards: (1) It is one of a very small number of proofs showing correctness of BP without any constraint on the graph structure. (2) Variants of the proof work for both synchronous and asynchronous BP; it is the first proof of convergence and correctness of an asynchronous BP algorithm for a combinatorial optimization problem.