A Kolmogorov-Arnold Neural Model for Cascading Extremes

This paper addresses the growing concern of cascading extreme events, such as an extreme earthquake followed by a tsunami, by presenting a novel method for risk assessment focused on these domino effects. The proposed approach develops an extreme value theory framework within a Kolmogorov-Arnold network (KAN) to estimate the probability of one extreme event triggering another, conditionally on a feature vector. An extra layer is added to the KAN's architecture to enforce the definition of the parameter of interest within the unit interval, and we refer to the resulting neural model as KANE (KAN with Natural Enforcement). The proposed method is backed by exhaustive numerical studies and further illustrated with real-world applications to seismology and climatology.

When a Reinforcement Learning Agent Encounters Unknown Unknowns

An AI agent might surprisingly find she has reached an unknown state which she has never been aware of -- an unknown unknown. We mathematically ground this scenario in reinforcement learning: an agent, after taking an action calculated from value functions $Q$ and $V$ defined on the {\it {aware domain}}, reaches a state out of the domain. To enable the agent to handle this scenario, we propose an {\it episodic Markov decision {process} with growing awareness} (EMDP-GA) model, taking a new {\it noninformative value expansion} (NIVE) approach to expand value functions to newly aware areas: when an agent arrives at an unknown unknown, value functions $Q$ and $V$ whereon are initialised by noninformative beliefs -- the averaged values on the aware domain. This design is out of respect for the complete absence of knowledge in the newly discovered state. The upper confidence bound momentum Q-learning is then adapted to the growing awareness for training the EMDP-GA model. We prove that (1) the regret of our approach is asymptotically consistent with the state of the art (SOTA) without exposure to unknown unknowns in an extremely uncertain environment, and (2) our computational complexity and space complexity are comparable with the SOTA -- these collectively suggest that though an unknown unknown is surprising, it will be asymptotically properly discovered with decent speed and an affordable cost.

Decoding AI: The inside story of data analysis in ChatGPT

As a result of recent advancements in generative AI, the field of Data Science is prone to various changes. This review critically examines the Data Analysis (DA) capabilities of ChatGPT assessing its performance across a wide range of tasks. While DA provides researchers and practitioners with unprecedented analytical capabilities, it is far from being perfect, and it is important to recognize and address its limitations.

A parallelizable model-based approach for marginal and multivariate clustering

This paper develops a clustering method that takes advantage of the sturdiness of model-based clustering, while attempting to mitigate some of its pitfalls. First, we note that standard model-based clustering likely leads to the same number of clusters per margin, which seems a rather artificial assumption for a variety of datasets. We tackle this issue by specifying a finite mixture model per margin that allows each margin to have a different number of clusters, and then cluster the multivariate data using a strategy game-inspired algorithm to which we call Reign-and-Conquer. Second, since the proposed clustering approach only specifies a model for the margins -- but leaves the joint unspecified -- it has the advantage of being partially parallelizable; hence, the proposed approach is computationally appealing as well as more tractable for moderate to high dimensions than a `full' (joint) model-based clustering approach. A battery of numerical experiments on artificial data indicate an overall good performance of the proposed methods in a variety of scenarios, and real datasets are used to showcase their application in practice.

Uncovering Regions of Maximum Dissimilarity on Random Process Data

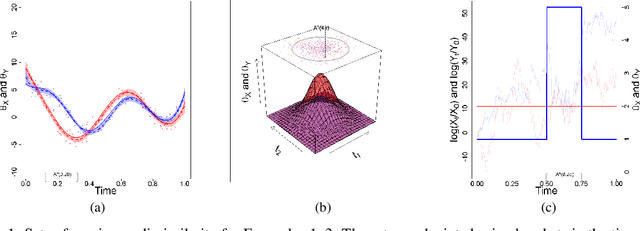
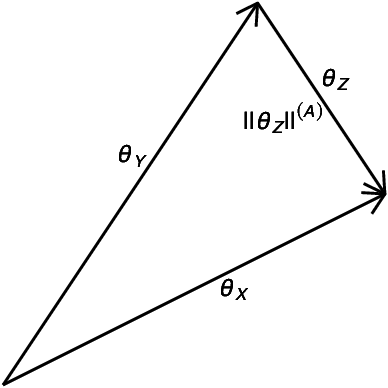
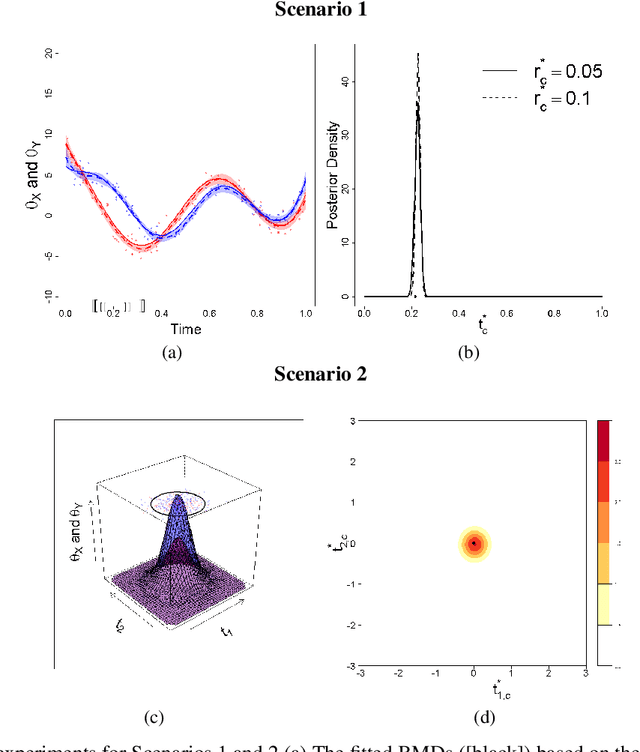
The comparison of local characteristics of two random processes can shed light on periods of time or space at which the processes differ the most. This paper proposes a method that learns about regions with a certain volume, where the marginal attributes of two processes are less similar. The proposed methods are devised in full generality for the setting where the data of interest are themselves stochastic processes, and thus the proposed method can be used for pointing out the regions of maximum dissimilarity with a certain volume, in the contexts of functional data, time series, and point processes. The parameter functions underlying both stochastic processes of interest are modeled via a basis representation, and Bayesian inference is conducted via an integrated nested Laplace approximation. The numerical studies validate the proposed methods, and we showcase their application with case studies on criminology, finance, and medicine.