Optimal Learning of Joint Alignments with a Faulty Oracle

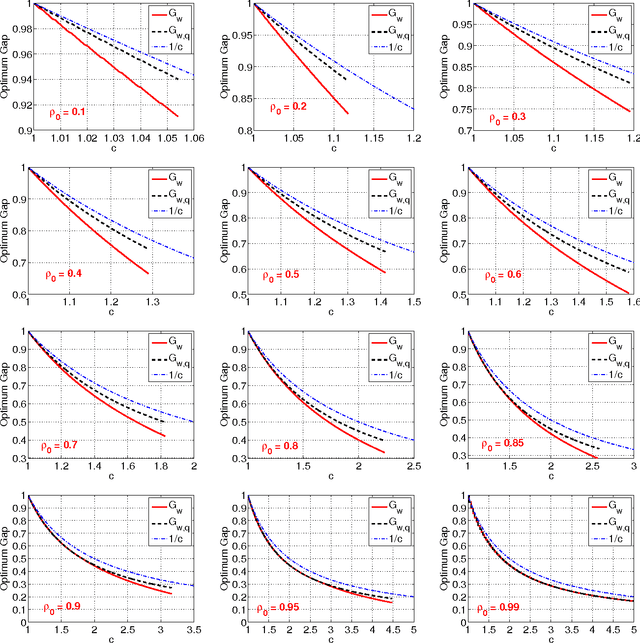
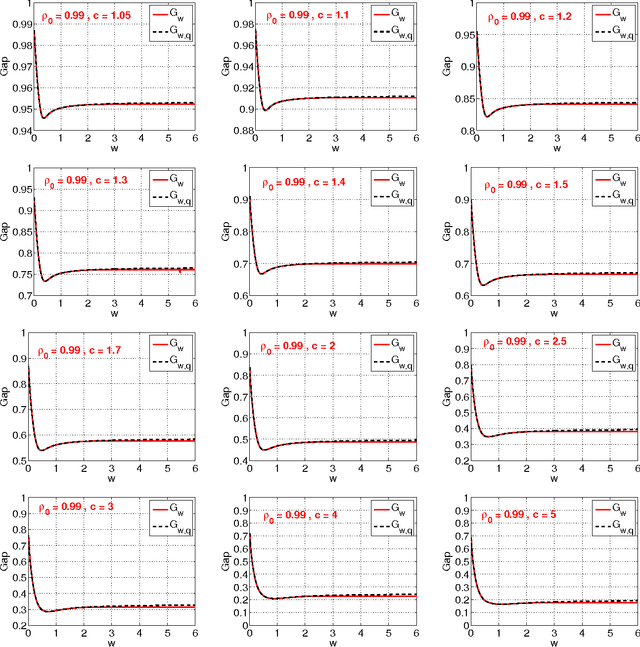
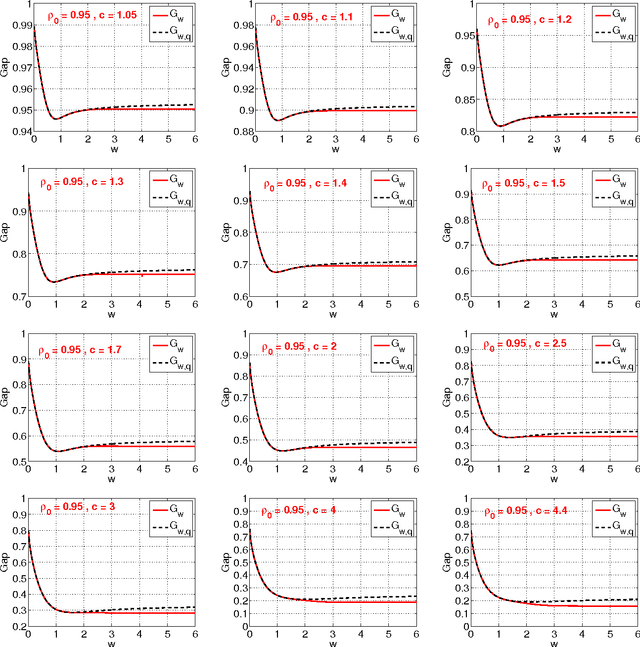
We consider the following problem, which is useful in applications such as joint image and shape alignment. The goal is to recover $n$ discrete variables $g_i \in \{0, \ldots, k-1\}$ (up to some global offset) given noisy observations of a set of their pairwise differences $\{(g_i - g_j) \bmod k\}$; specifically, with probability $\frac{1}{k}+\delta$ for some $\delta > 0$ one obtains the correct answer, and with the remaining probability one obtains a uniformly random incorrect answer. We consider a learning-based formulation where one can perform a query to observe a pairwise difference, and the goal is to perform as few queries as possible while obtaining the exact joint alignment. We provide an easy-to-implement, time efficient algorithm that performs $O\big(\frac{n \lg n}{k \delta^2}\big)$ queries, and recovers the joint alignment with high probability. We also show that our algorithm is optimal by proving a general lower bound that holds for all non-adaptive algorithms. Our work improves significantly recent work by Chen and Cand\'{e}s \cite{chen2016projected}, who view the problem as a constrained principal components analysis problem that can be solved using the power method. Specifically, our approach is simpler both in the algorithm and the analysis, and provides additional insights into the problem structure.

The Supermarket Model with Known and Predicted Service Times

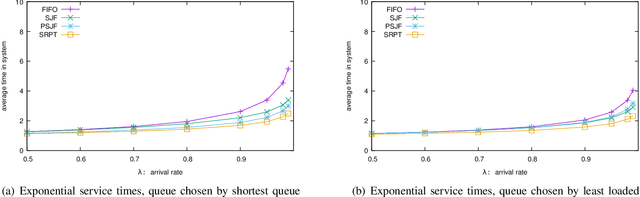
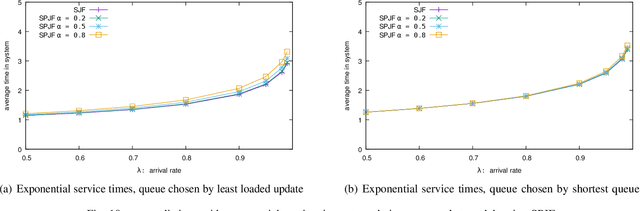
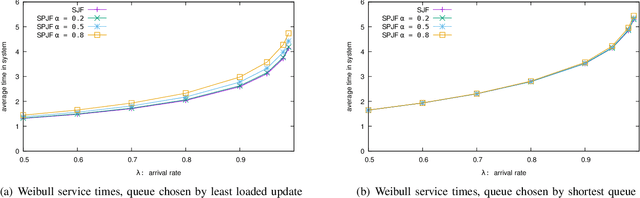
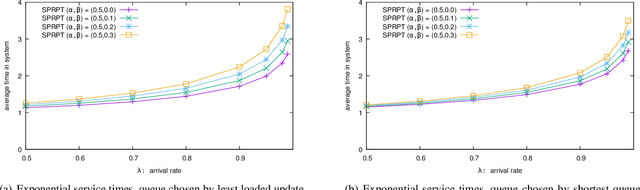
The supermarket model typically refers to a system with a large number of queues, where arriving customers choose $d$ queues at random and join the queue with fewest customers. The supermarket model demonstrates the power of even small amounts of choice, as compared to simply joining a queue chosen uniformly at random, for load balancing systems. In this work we perform simulation-based studies to consider variations where service times for a customer are predicted, as might be done in modern settings using machine learning techniques or related mechanisms. To begin, we start by considering the baseline where service times are known. We find that this allows for significant improvements. In particular, not only can the queue being joined be chosen based on the total work at the queue instead of the number of jobs, but also the jobs in the queue can be served using strategies that take advantage of the service times such as shortest job first or shortest remaining processing time. Such strategies greatly improve performance under high load. We then examine the impact of using predictions in place of true service times. Our main takeaway is that using even seemingly weak predictions of service times can yield significant benefits over blind First In First Out queueing in this context. However, some care must be taken when using predicted service time information to both choose a queue and order elements for service within a queue; while in many cases using the information for both choosing and ordering is beneficial, in many of our simulation settings we find that simply using the number of jobs to choose a queue is better when using predicted service times to order jobs in a queue. Our study leaves many natural open questions for further work.

Online Pandora's Boxes and Bandits

We consider online variations of the Pandora's box problem (Weitzman. 1979), a standard model for understanding issues related to the cost of acquiring information for decision-making. Our problem generalizes both the classic Pandora's box problem and the prophet inequality framework. Boxes are presented online, each with a random value and cost drew jointly from some known distribution. Pandora chooses online whether to open each box given its cost, and then chooses irrevocably whether to keep the revealed prize or pass on it. We aim for approximation algorithms against adversaries that can choose the largest prize over any opened box, and use optimal offline policies to decide which boxes to open (without knowledge of the value inside). We consider variations where Pandora can collect multiple prizes subject to feasibility constraints, such as cardinality, matroid, or knapsack constraints. We also consider variations related to classic multi-armed bandit problems from reinforcement learning. Our results use a reduction-based framework where we separate the issues of the cost of acquiring information from the online decision process of which prizes to keep. Our work shows that in many scenarios, Pandora can achieve a good approximation to the best possible performance.

A Model for Learned Bloom Filters, and Optimizing by Sandwiching

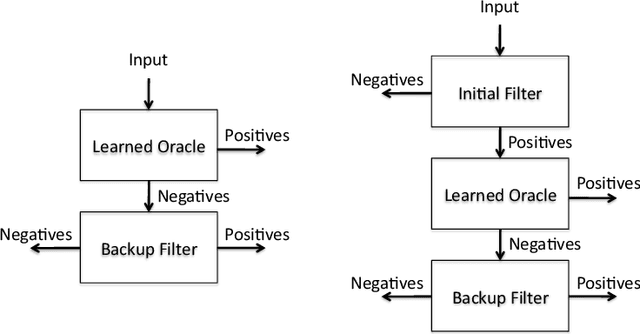
Recent work has suggested enhancing Bloom filters by using a pre-filter, based on applying machine learning to determine a function that models the data set the Bloom filter is meant to represent. Here we model such learned Bloom filters,, with the following outcomes: (1) we clarify what guarantees can and cannot be associated with such a structure; (2) we show how to estimate what size the learning function must obtain in order to obtain improved performance; (3) we provide a simple method, sandwiching, for optimizing learned Bloom filters; and (4) we propose a design and analysis approach for a learned Bloomier filter, based on our modeling approach.

Predicting Positive and Negative Links with Noisy Queries: Theory & Practice

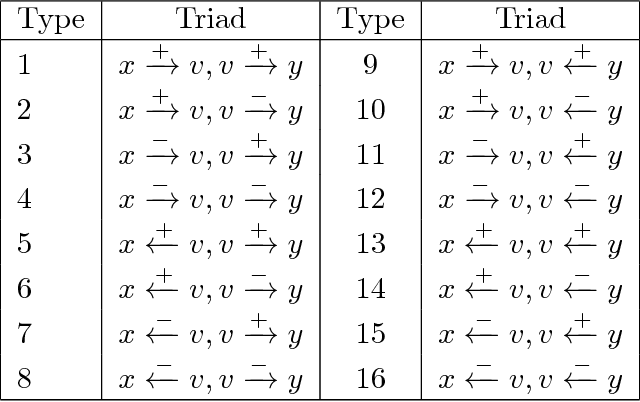
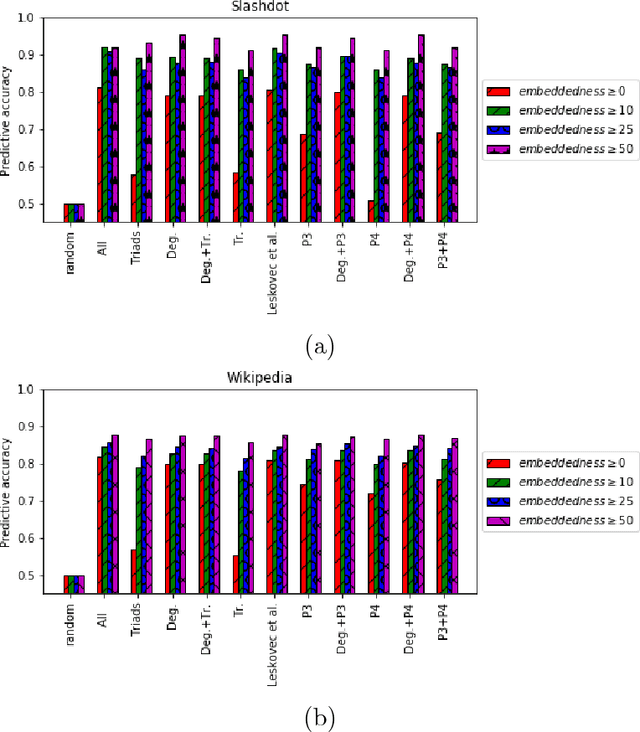
Social networks involve both positive and negative relationships, which can be captured in signed graphs. The {\em edge sign prediction problem} aims to predict whether an interaction between a pair of nodes will be positive or negative. We provide theoretical results for this problem that motivate natural improvements to recent heuristics. The edge sign prediction problem is related to correlation clustering; a positive relationship means being in the same cluster. We consider the following model for two clusters: we are allowed to query any pair of nodes whether they belong to the same cluster or not, but the answer to the query is corrupted with some probability $0<q<\frac{1}{2}$. Let $\delta=1-2q$ be the bias. We provide an algorithm that recovers all signs correctly with high probability in the presence of noise with $O(\frac{n\log n}{\delta^2}+\frac{\log^2 n}{\delta^6})$ queries. This is the best known result for this problem for all but tiny $\delta$, improving on the recent work of Mazumdar and Saha \cite{mazumdar2017clustering}. We also provide an algorithm that performs $O(\frac{n\log n}{\delta^4})$ queries, and uses breadth first search as its main algorithmic primitive. While both the running time and the number of queries for this algorithm are sub-optimal, our result relies on novel theoretical techniques, and naturally suggests the use of edge-disjoint paths as a feature for predicting signs in online social networks. Correspondingly, we experiment with using edge disjoint $s-t$ paths of short length as a feature for predicting the sign of edge $(s,t)$ in real-world signed networks. Empirical findings suggest that the use of such paths improves the classification accuracy, especially for pairs of nodes with no common neighbors.

2-Bit Random Projections, NonLinear Estimators, and Approximate Near Neighbor Search

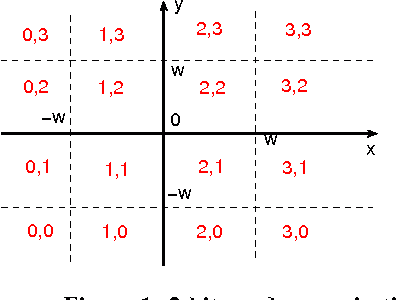
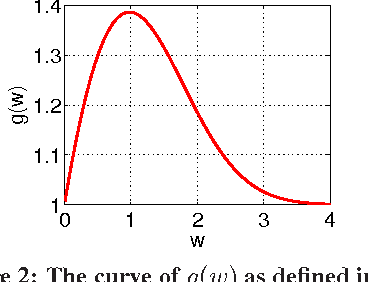
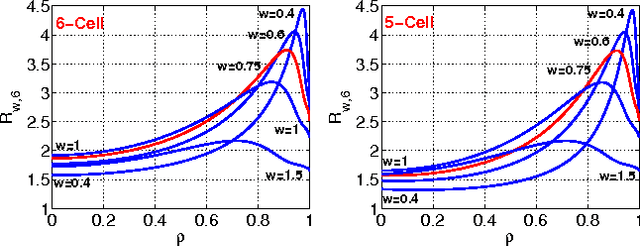
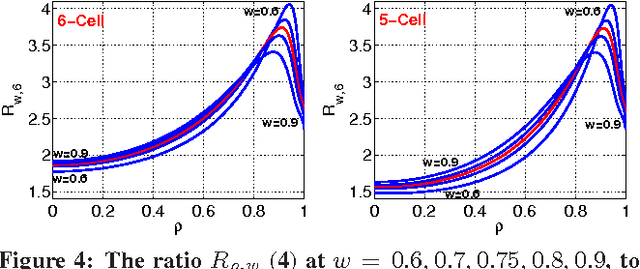
The method of random projections has become a standard tool for machine learning, data mining, and search with massive data at Web scale. The effective use of random projections requires efficient coding schemes for quantizing (real-valued) projected data into integers. In this paper, we focus on a simple 2-bit coding scheme. In particular, we develop accurate nonlinear estimators of data similarity based on the 2-bit strategy. This work will have important practical applications. For example, in the task of near neighbor search, a crucial step (often called re-ranking) is to compute or estimate data similarities once a set of candidate data points have been identified by hash table techniques. This re-ranking step can take advantage of the proposed coding scheme and estimator. As a related task, in this paper, we also study a simple uniform quantization scheme for the purpose of building hash tables with projected data. Our analysis shows that typically only a small number of bits are needed. For example, when the target similarity level is high, 2 or 3 bits might be sufficient. When the target similarity level is not so high, it is preferable to use only 1 or 2 bits. Therefore, a 2-bit scheme appears to be overall a good choice for the task of sublinear time approximate near neighbor search via hash tables. Combining these results, we conclude that 2-bit random projections should be recommended for approximate near neighbor search and similarity estimation. Extensive experimental results are provided.

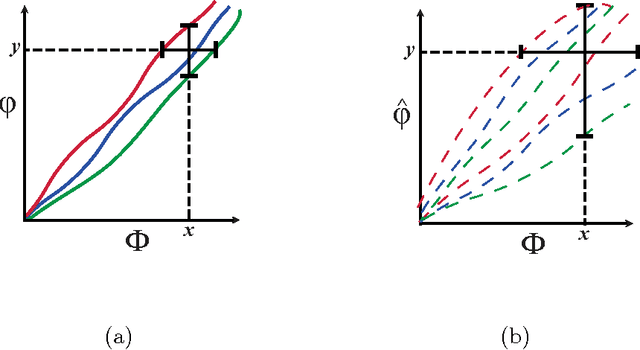
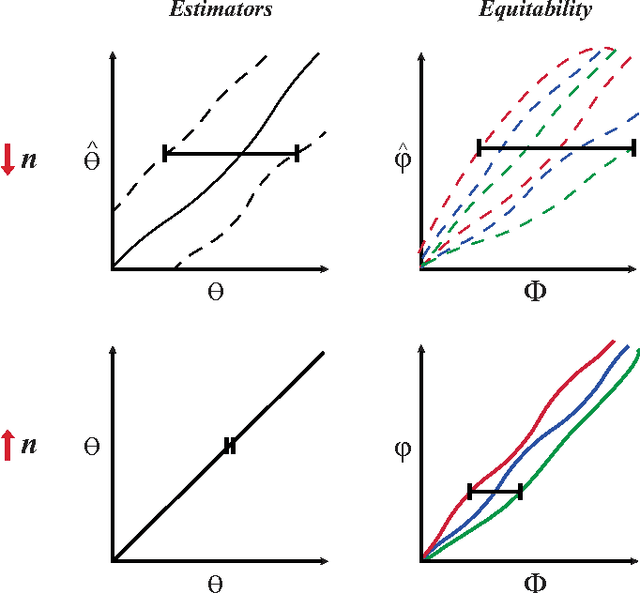
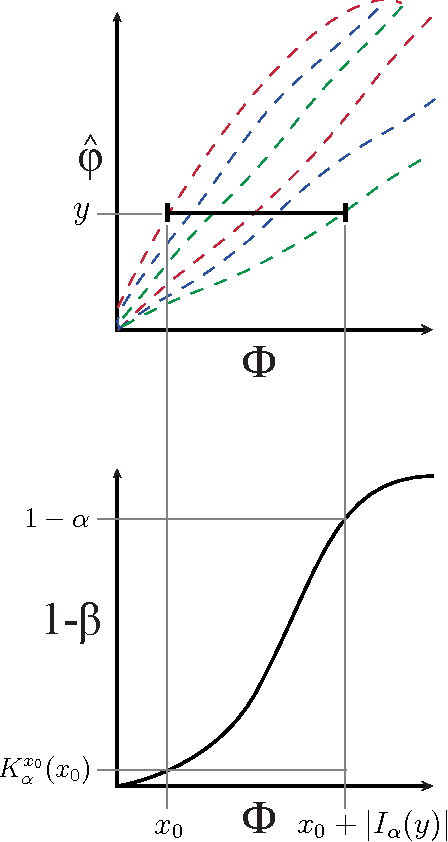
Theoretical Foundations of Equitability and the Maximal Information Coefficient

The maximal information coefficient (MIC) is a tool for finding the strongest pairwise relationships in a data set with many variables (Reshef et al., 2011). MIC is useful because it gives similar scores to equally noisy relationships of different types. This property, called {\em equitability}, is important for analyzing high-dimensional data sets. Here we formalize the theory behind both equitability and MIC in the language of estimation theory. This formalization has a number of advantages. First, it allows us to show that equitability is a generalization of power against statistical independence. Second, it allows us to compute and discuss the population value of MIC, which we call MIC_*. In doing so we generalize and strengthen the mathematical results proven in Reshef et al. (2011) and clarify the relationship between MIC and mutual information. Introducing MIC_* also enables us to reason about the properties of MIC more abstractly: for instance, we show that MIC_* is continuous and that there is a sense in which it is a canonical "smoothing" of mutual information. We also prove an alternate, equivalent characterization of MIC_* that we use to state new estimators of it as well as an algorithm for explicitly computing it when the joint probability density function of a pair of random variables is known. Our hope is that this paper provides a richer theoretical foundation for MIC and equitability going forward. This paper will be accompanied by a forthcoming companion paper that performs extensive empirical analysis and comparison to other methods and discusses the practical aspects of both equitability and the use of MIC and its related statistics.

Coding for Random Projections and Approximate Near Neighbor Search

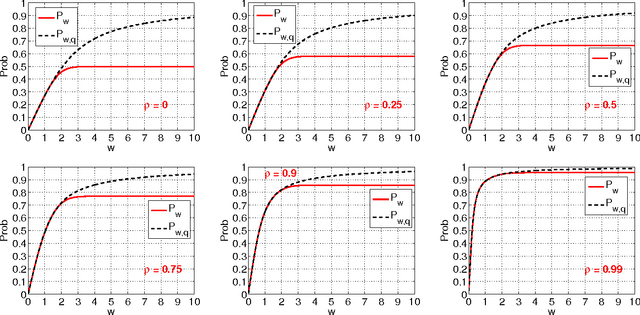
This technical note compares two coding (quantization) schemes for random projections in the context of sub-linear time approximate near neighbor search. The first scheme is based on uniform quantization while the second scheme utilizes a uniform quantization plus a uniformly random offset (which has been popular in practice). The prior work compared the two schemes in the context of similarity estimation and training linear classifiers, with the conclusion that the step of random offset is not necessary and may hurt the performance (depending on the similarity level). The task of near neighbor search is related to similarity estimation with importance distinctions and requires own study. In this paper, we demonstrate that in the context of near neighbor search, the step of random offset is not needed either and may hurt the performance (sometimes significantly so, depending on the similarity and other parameters).

Equitability Analysis of the Maximal Information Coefficient, with Comparisons

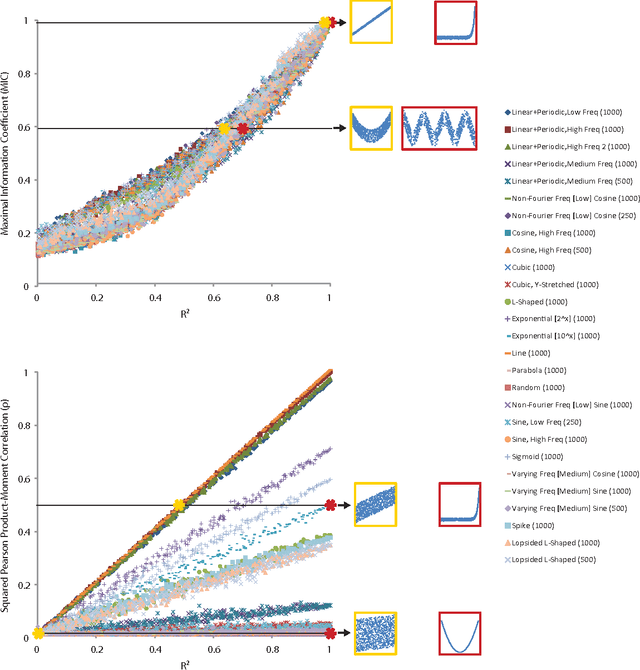
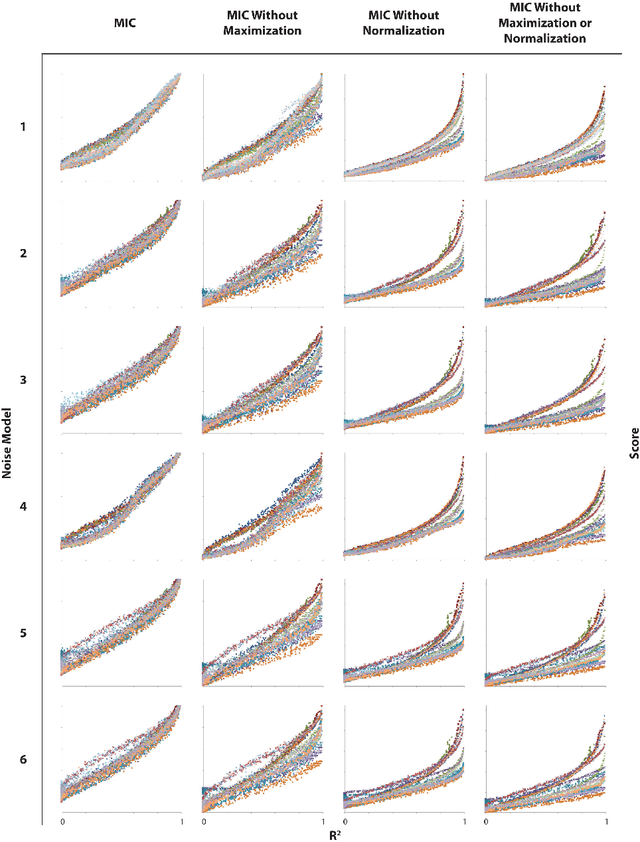
A measure of dependence is said to be equitable if it gives similar scores to equally noisy relationships of different types. Equitability is important in data exploration when the goal is to identify a relatively small set of strongest associations within a dataset as opposed to finding as many non-zero associations as possible, which often are too many to sift through. Thus an equitable statistic, such as the maximal information coefficient (MIC), can be useful for analyzing high-dimensional data sets. Here, we explore both equitability and the properties of MIC, and discuss several aspects of the theory and practice of MIC. We begin by presenting an intuition behind the equitability of MIC through the exploration of the maximization and normalization steps in its definition. We then examine the speed and optimality of the approximation algorithm used to compute MIC, and suggest some directions for improving both. Finally, we demonstrate in a range of noise models and sample sizes that MIC is more equitable than natural alternatives, such as mutual information estimation and distance correlation.

Coding for Random Projections

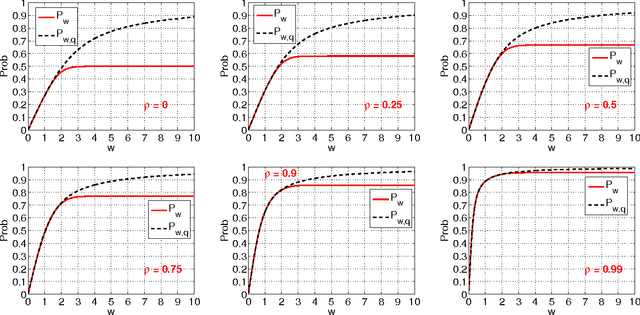
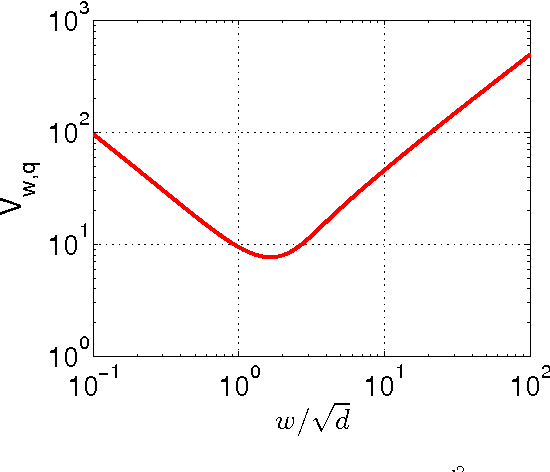
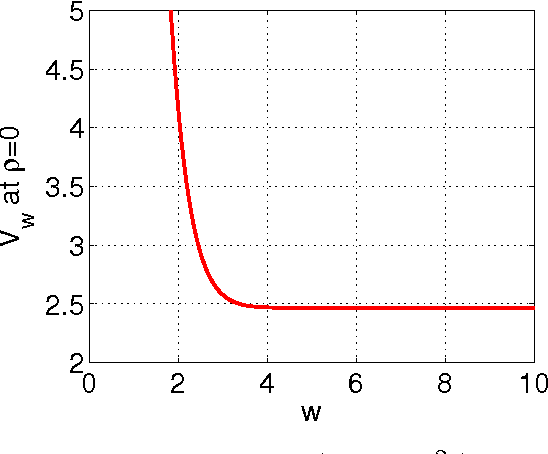
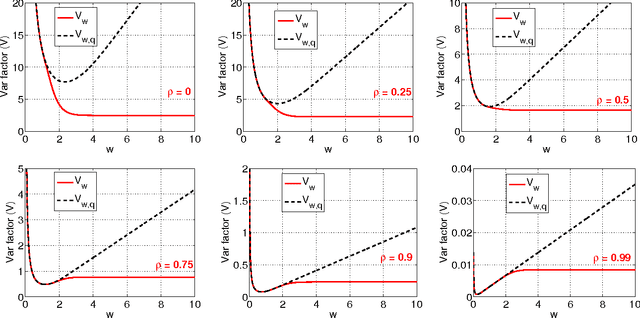
The method of random projections has become very popular for large-scale applications in statistical learning, information retrieval, bio-informatics and other applications. Using a well-designed coding scheme for the projected data, which determines the number of bits needed for each projected value and how to allocate these bits, can significantly improve the effectiveness of the algorithm, in storage cost as well as computational speed. In this paper, we study a number of simple coding schemes, focusing on the task of similarity estimation and on an application to training linear classifiers. We demonstrate that uniform quantization outperforms the standard existing influential method (Datar et. al. 2004). Indeed, we argue that in many cases coding with just a small number of bits suffices. Furthermore, we also develop a non-uniform 2-bit coding scheme that generally performs well in practice, as confirmed by our experiments on training linear support vector machines (SVM).