Michael Kommenda
Vectorial Genetic Programming -- Optimizing Segments for Feature Extraction
Mar 03, 2023



Abstract:Vectorial Genetic Programming (Vec-GP) extends GP by allowing vectors as input features along regular, scalar features, using them by applying arithmetic operations component-wise or aggregating vectors into scalars by some aggregation function. Vec-GP also allows aggregating vectors only over a limited segment of the vector instead of the whole vector, which offers great potential but also introduces new parameters that GP has to optimize. This paper formalizes an optimization problem to analyze different strategies for optimizing a window for aggregation functions. Different strategies are presented, included random and guided sampling, where the latter leverages information from an approximated gradient. Those strategies can be applied as a simple optimization algorithm, which itself ca be applied inside a specialized mutation operator within GP. The presented results indicate, that the different random sampling strategies do not impact the overall algorithm performance significantly, and that the guided strategies suffer from becoming stuck in local optima. However, results also indicate, that there is still potential in discovering more efficient algorithms that could outperform the presented strategies.
Symbolic Regression with Fast Function Extraction and Nonlinear Least Squares Optimization
Sep 20, 2022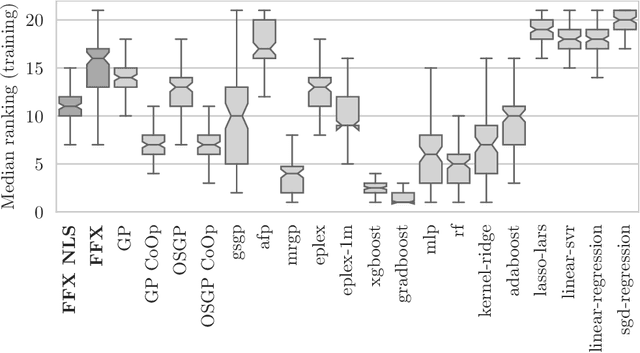
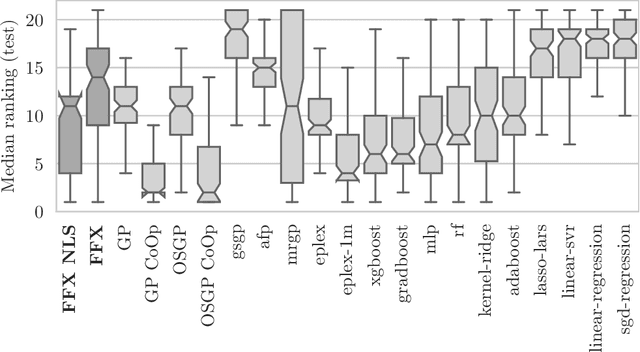
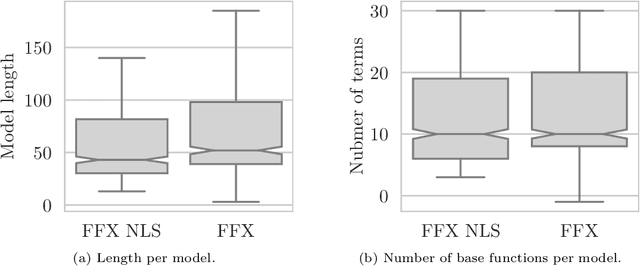
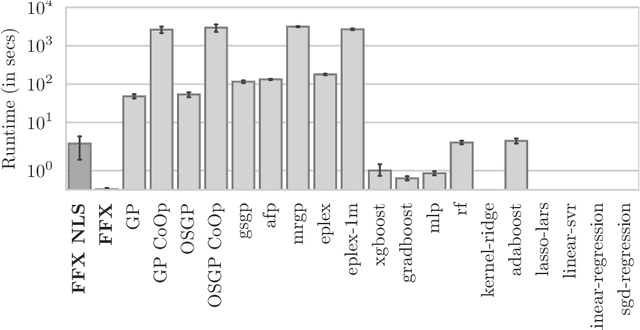
Abstract:Fast Function Extraction (FFX) is a deterministic algorithm for solving symbolic regression problems. We improve the accuracy of FFX by adding parameters to the arguments of nonlinear functions. Instead of only optimizing linear parameters, we optimize these additional nonlinear parameters with separable nonlinear least squared optimization using a variable projection algorithm. Both FFX and our new algorithm is applied on the PennML benchmark suite. We show that the proposed extensions of FFX leads to higher accuracy while providing models of similar length and with only a small increase in runtime on the given data. Our results are compared to a large set of regression methods that were already published for the given benchmark suite.
Symbolic Regression in Materials Science: Discovering Interatomic Potentials from Data
Jun 13, 2022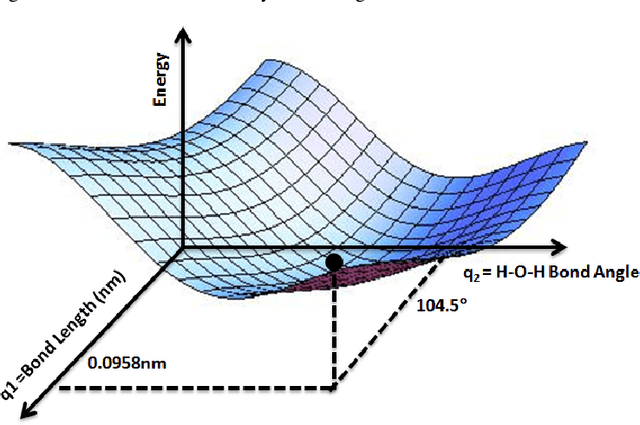

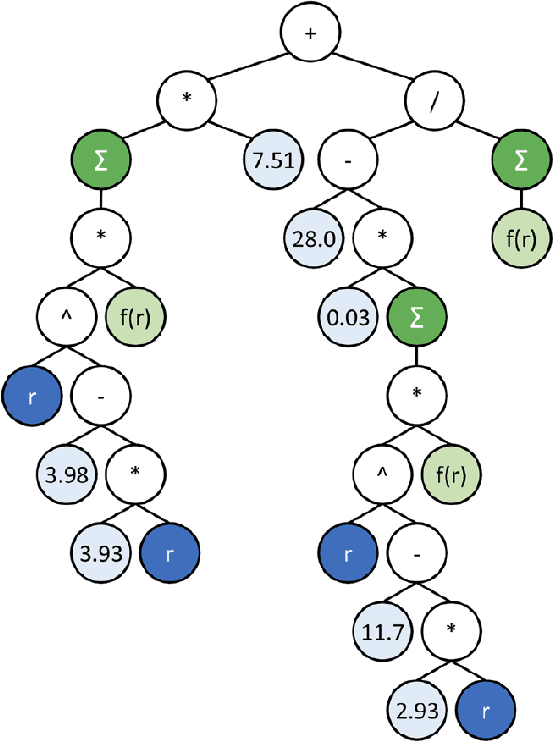
Abstract:Particle-based modeling of materials at atomic scale plays an important role in the development of new materials and understanding of their properties. The accuracy of particle simulations is determined by interatomic potentials, which allow to calculate the potential energy of an atomic system as a function of atomic coordinates and potentially other properties. First-principles-based ab initio potentials can reach arbitrary levels of accuracy, however their aplicability is limited by their high computational cost. Machine learning (ML) has recently emerged as an effective way to offset the high computational costs of ab initio atomic potentials by replacing expensive models with highly efficient surrogates trained on electronic structure data. Among a plethora of current methods, symbolic regression (SR) is gaining traction as a powerful "white-box" approach for discovering functional forms of interatomic potentials. This contribution discusses the role of symbolic regression in Materials Science (MS) and offers a comprehensive overview of current methodological challenges and state-of-the-art results. A genetic programming-based approach for modeling atomic potentials from raw data (consisting of snapshots of atomic positions and associated potential energy) is presented and empirically validated on ab initio electronic structure data.
Cluster Analysis of a Symbolic Regression Search Space
Sep 28, 2021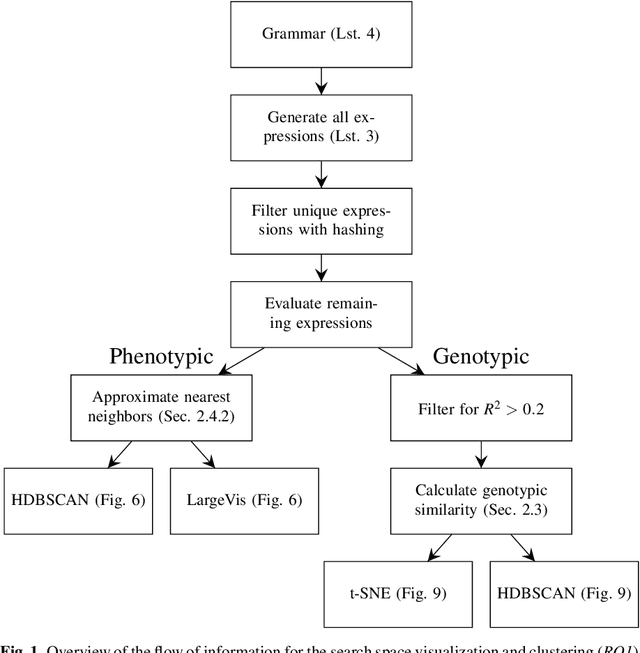
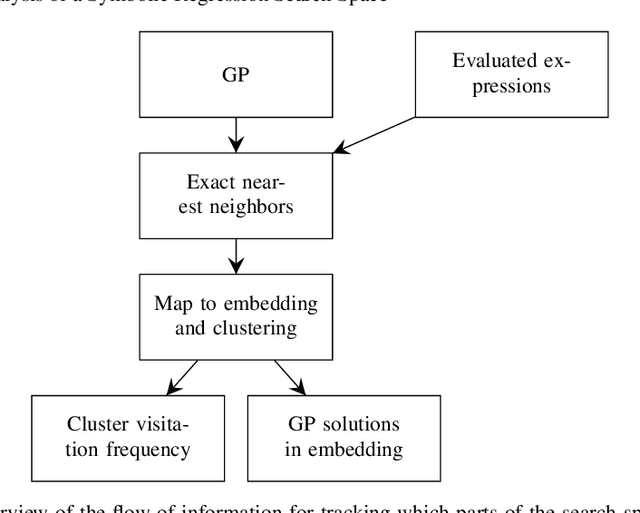

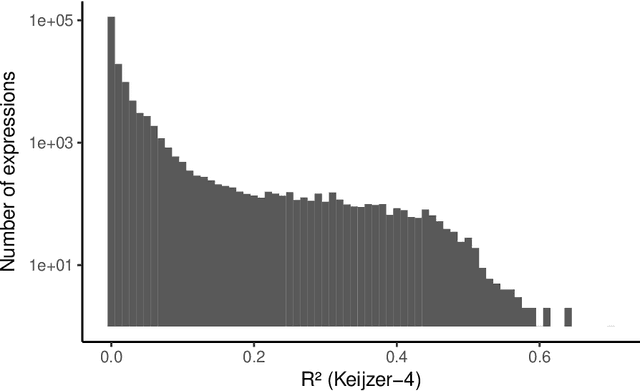
Abstract:In this chapter we take a closer look at the distribution of symbolic regression models generated by genetic programming in the search space. The motivation for this work is to improve the search for well-fitting symbolic regression models by using information about the similarity of models that can be precomputed independently from the target function. For our analysis, we use a restricted grammar for uni-variate symbolic regression models and generate all possible models up to a fixed length limit. We identify unique models and cluster them based on phenotypic as well as genotypic similarity. We find that phenotypic similarity leads to well-defined clusters while genotypic similarity does not produce a clear clustering. By mapping solution candidates visited by GP to the enumerated search space we find that GP initially explores the whole search space and later converges to the subspace of highest quality expressions in a run for a simple benchmark problem.
* Genetic Programming Theory and Practice XVI. Genetic and Evolutionary Computation. Springer
Symbolic Regression by Exhaustive Search: Reducing the Search Space Using Syntactical Constraints and Efficient Semantic Structure Deduplication
Sep 28, 2021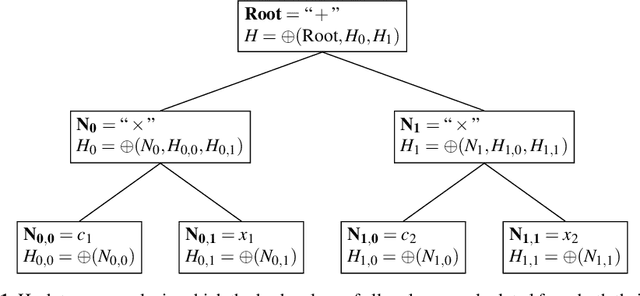

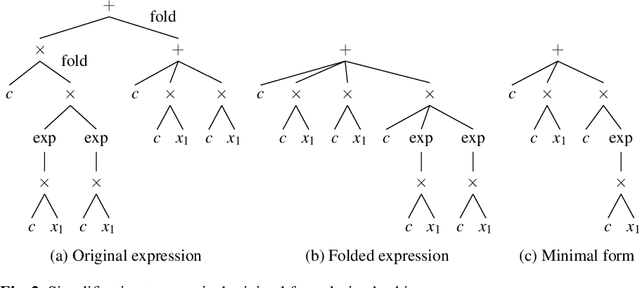

Abstract:Symbolic regression is a powerful system identification technique in industrial scenarios where no prior knowledge on model structure is available. Such scenarios often require specific model properties such as interpretability, robustness, trustworthiness and plausibility, that are not easily achievable using standard approaches like genetic programming for symbolic regression. In this chapter we introduce a deterministic symbolic regression algorithm specifically designed to address these issues. The algorithm uses a context-free grammar to produce models that are parameterized by a non-linear least squares local optimization procedure. A finite enumeration of all possible models is guaranteed by structural restrictions as well as a caching mechanism for detecting semantically equivalent solutions. Enumeration order is established via heuristics designed to improve search efficiency. Empirical tests on a comprehensive benchmark suite show that our approach is competitive with genetic programming in many noiseless problems while maintaining desirable properties such as simple, reliable models and reproducibility.
* Genetic and Evolutionary Computation
Understanding and Preparing Data of Industrial Processes for Machine Learning Applications
Sep 08, 2021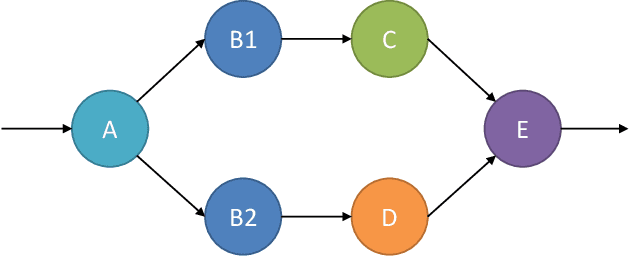

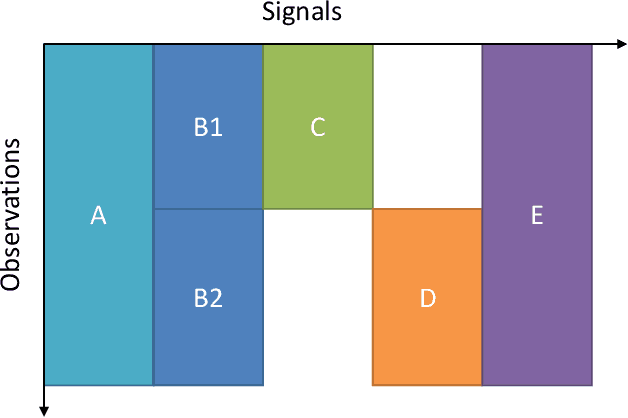
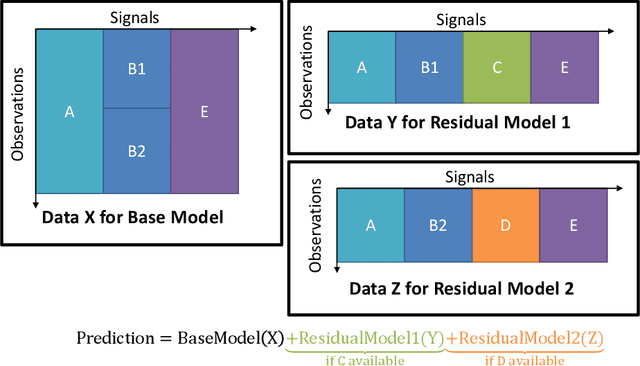
Abstract:Industrial applications of machine learning face unique challenges due to the nature of raw industry data. Preprocessing and preparing raw industrial data for machine learning applications is a demanding task that often takes more time and work than the actual modeling process itself and poses additional challenges. This paper addresses one of those challenges, specifically, the challenge of missing values due to sensor unavailability at different production units of nonlinear production lines. In cases where only a small proportion of the data is missing, those missing values can often be imputed. In cases of large proportions of missing data, imputing is often not feasible, and removing observations containing missing values is often the only option. This paper presents a technique, that allows to utilize all of the available data without the need of removing large amounts of observations where data is only partially available. We do not only discuss the principal idea of the presented method, but also show different possible implementations that can be applied depending on the data at hand. Finally, we demonstrate the application of the presented method with data from a steel production plant.
* International Conference on Computer Aided Systems Theory, Eurocast 2019, pp 413-420
Preprocessing and Modeling of Radial Fan Data for Health State Prediction
Sep 08, 2021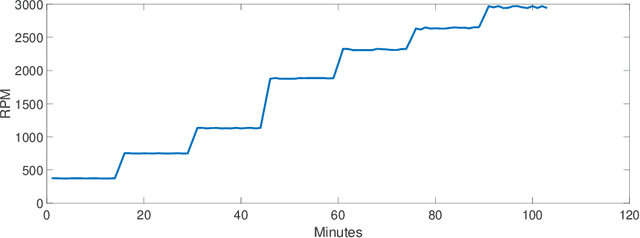
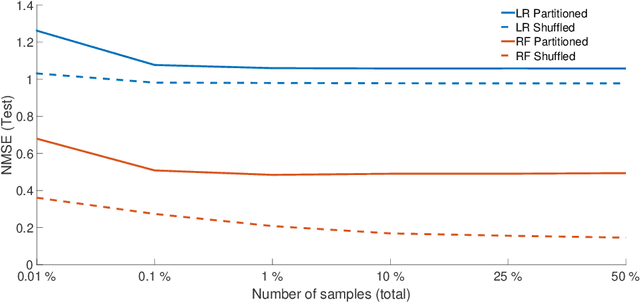
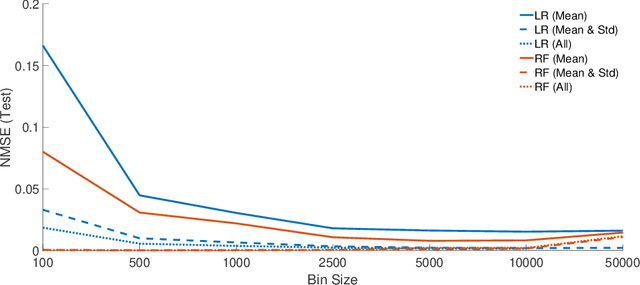
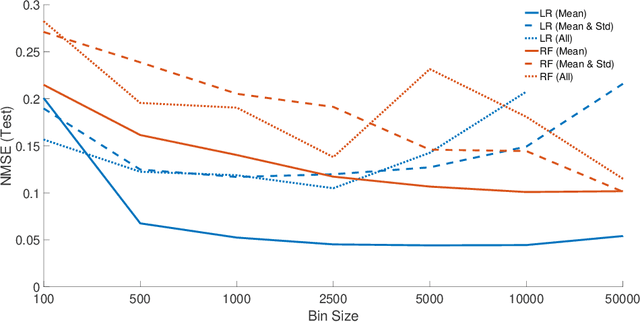
Abstract:Monitoring critical components of systems is a crucial step towards failure safety. Affordable sensors are available and the industry is in the process of introducing and extending monitoring solutions to improve product quality. Often, no expertise of how much data is required for a certain task (e.g. monitoring) exists. Especially in vital machinery, a trend to exaggerated sensors may be noticed, both in quality and in quantity. This often results in an excessive generation of data, which should be transferred, processed and stored nonetheless. In a previous case study, several sensors have been mounted on a healthy radial fan, which was later artificially damaged. The gathered data was used for modeling (and therefore monitoring) a healthy state. The models were evaluated on a dataset created by using a faulty impeller. This paper focuses on the reduction of this data through downsampling and binning. Different models are created with linear regression and random forest regression and the resulting difference in quality is discussed.
* International Conference on Computer Aided Systems Theory, Eurocast 2019, pp 312-318
Complexity Measures for Multi-objective Symbolic Regression
Sep 01, 2021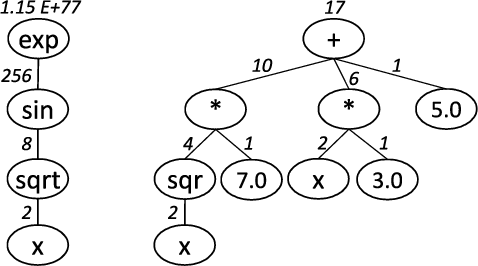
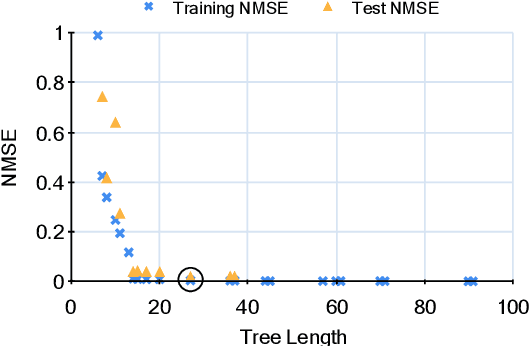
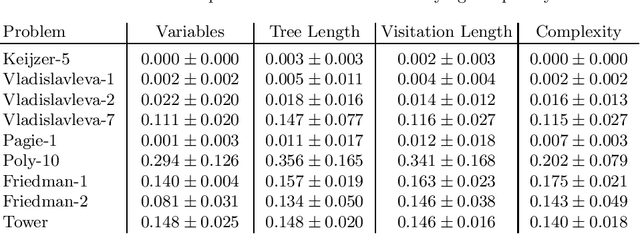
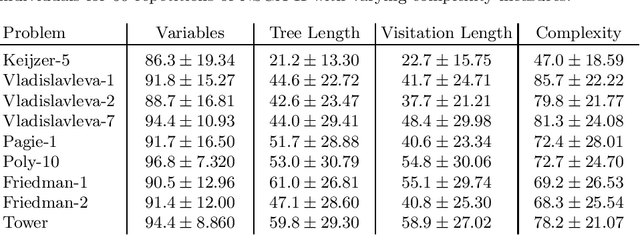
Abstract:Multi-objective symbolic regression has the advantage that while the accuracy of the learned models is maximized, the complexity is automatically adapted and need not be specified a-priori. The result of the optimization is not a single solution anymore, but a whole Pareto-front describing the trade-off between accuracy and complexity. In this contribution we study which complexity measures are most appropriately used in symbolic regression when performing multi- objective optimization with NSGA-II. Furthermore, we present a novel complexity measure that includes semantic information based on the function symbols occurring in the models and test its effects on several benchmark datasets. Results comparing multiple complexity measures are presented in terms of the achieved accuracy and model length to illustrate how the search direction of the algorithm is affected.
* International Conference on Computer Aided Systems Theory, Eurocast 2015, pp 409-416
On the Effectiveness of Genetic Operations in Symbolic Regression
Aug 24, 2021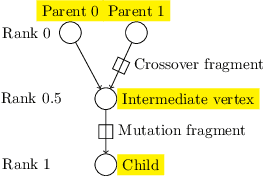
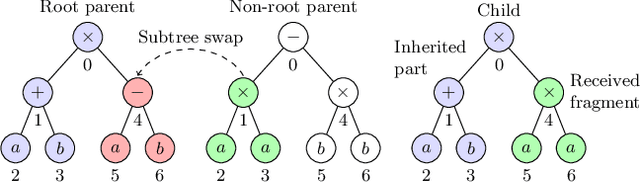
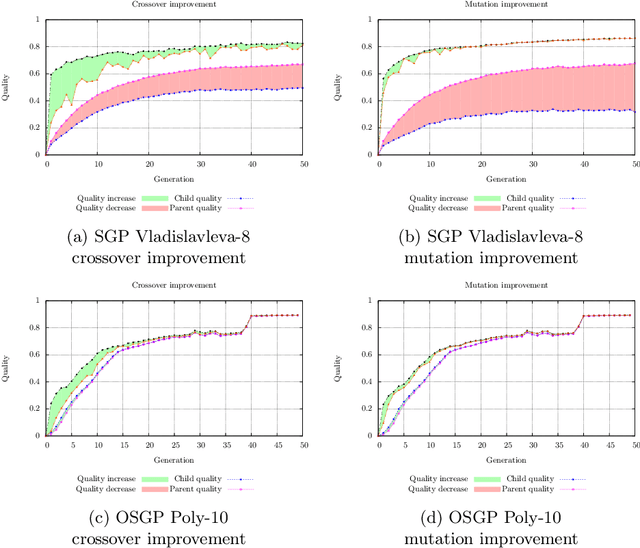
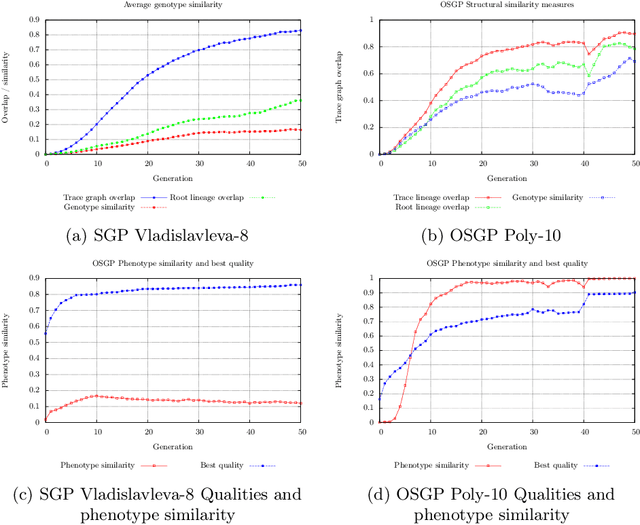
Abstract:This paper describes a methodology for analyzing the evolutionary dynamics of genetic programming (GP) using genealogical information, diversity measures and information about the fitness variation from parent to offspring. We introduce a new subtree tracing approach for identifying the origins of genes in the structure of individuals, and we show that only a small fraction of ancestor individuals are responsible for the evolvement of the best solutions in the population.
* International Conference on Computer Aided Systems Theory, Eurocast 2015, pp 367-374
Data Aggregation for Reducing Training Data in Symbolic Regression
Aug 24, 2021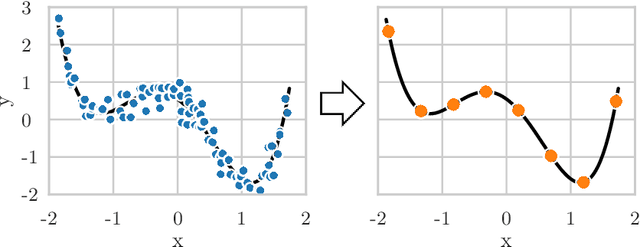
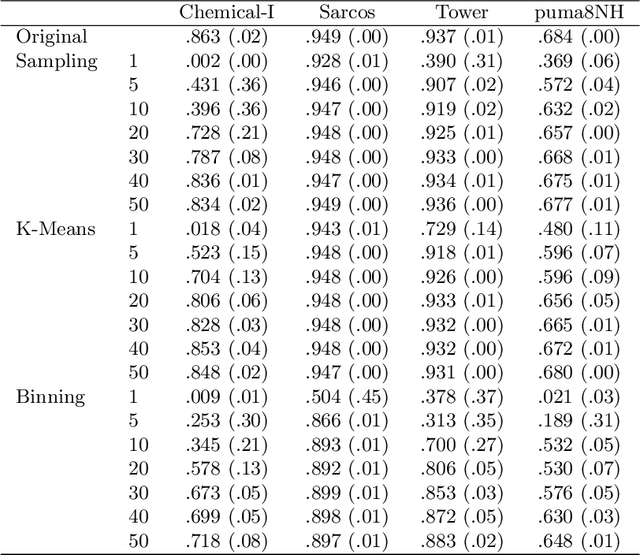
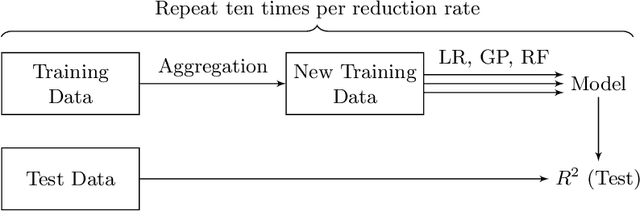
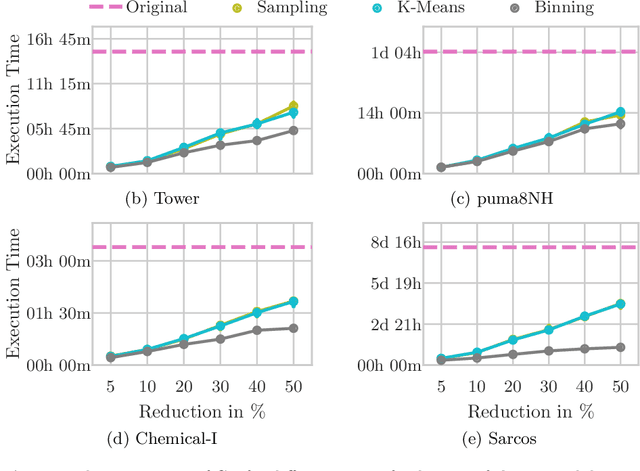
Abstract:The growing volume of data makes the use of computationally intense machine learning techniques such as symbolic regression with genetic programming more and more impractical. This work discusses methods to reduce the training data and thereby also the runtime of genetic programming. The data is aggregated in a preprocessing step before running the actual machine learning algorithm. K-means clustering and data binning is used for data aggregation and compared with random sampling as the simplest data reduction method. We analyze the achieved speed-up in training and the effects on the trained models test accuracy for every method on four real-world data sets. The performance of genetic programming is compared with random forests and linear regression. It is shown, that k-means and random sampling lead to very small loss in test accuracy when the data is reduced down to only 30% of the original data, while the speed-up is proportional to the size of the data set. Binning on the contrary, leads to models with very high test error.
* International Conference on Computer Aided Systems Theory 2015, pp 378-386
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge