Gabriel Kronberger
Introduction to Symbolic Regression in the Physical Sciences
Dec 17, 2025Abstract:Symbolic regression (SR) has emerged as a powerful method for uncovering interpretable mathematical relationships from data, offering a novel route to both scientific discovery and efficient empirical modelling. This article introduces the Special Issue on Symbolic Regression for the Physical Sciences, motivated by the Royal Society discussion meeting held in April 2025. The contributions collected here span applications from automated equation discovery and emergent-phenomena modelling to the construction of compact emulators for computationally expensive simulations. The introductory review outlines the conceptual foundations of SR, contrasts it with conventional regression approaches, and surveys its main use cases in the physical sciences, including the derivation of effective theories, empirical functional forms and surrogate models. We summarise methodological considerations such as search-space design, operator selection, complexity control, feature selection, and integration with modern AI approaches. We also highlight ongoing challenges, including scalability, robustness to noise, overfitting and computational complexity. Finally we emphasise emerging directions, particularly the incorporation of symmetry constraints, asymptotic behaviour and other theoretical information. Taken together, the papers in this Special Issue illustrate the accelerating progress of SR and its growing relevance across the physical sciences.
Identification of Empirical Constitutive Models for Age-Hardenable Aluminium Alloy and High-Chromium Martensitic Steel Using Symbolic Regression
Nov 11, 2025
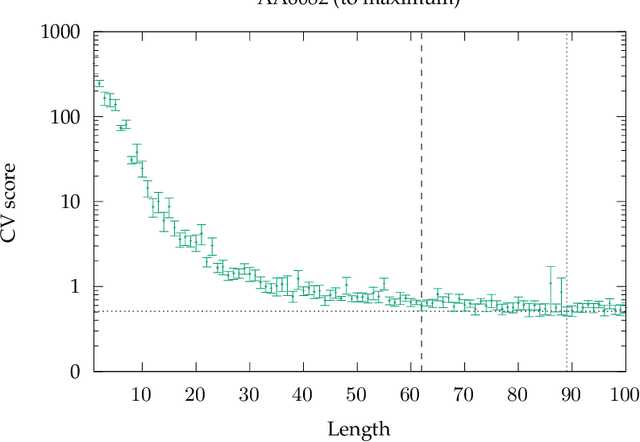

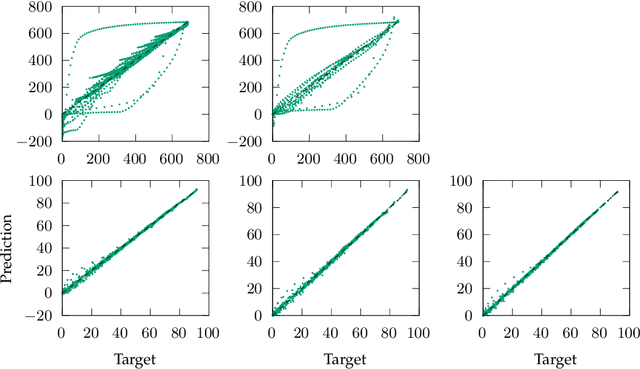
Abstract:Process-structure-property relationships are fundamental in materials science and engineering and are key to the development of new and improved materials. Symbolic regression serves as a powerful tool for uncovering mathematical models that describe these relationships. It can automatically generate equations to predict material behaviour under specific manufacturing conditions and optimize performance characteristics such as strength and elasticity. The present work illustrates how symbolic regression can derive constitutive models that describe the behaviour of various metallic alloys during plastic deformation. Constitutive modelling is a mathematical framework for understanding the relationship between stress and strain in materials under different loading conditions. In this study, two materials (age-hardenable aluminium alloy and high-chromium martensitic steel) and two different testing methods (compression and tension) are considered to obtain the required stress-strain data. The results highlight the benefits of using symbolic regression while also discussing potential challenges.
syren-baryon: Analytic emulators for the impact of baryons on the matter power spectrum
Jun 10, 2025Abstract:Baryonic physics has a considerable impact on the distribution of matter in our Universe on scales probed by current and future cosmological surveys, acting as a key systematic in such analyses. We seek simple symbolic parametrisations for the impact of baryonic physics on the matter power spectrum for a range of physically motivated models, as a function of wavenumber, redshift, cosmology, and parameters controlling the baryonic feedback. We use symbolic regression to construct analytic approximations for the ratio of the matter power spectrum in the presence of baryons to that without such effects. We obtain separate functions of each of four distinct sub-grid prescriptions of baryonic physics from the CAMELS suite of hydrodynamical simulations (Astrid, IllustrisTNG, SIMBA and Swift-EAGLE) as well as for a baryonification algorithm. We also provide functions which describe the uncertainty on these predictions, due to both the stochastic nature of baryonic physics and the errors on our fits. The error on our approximations to the hydrodynamical simulations is comparable to the sample variance estimated through varying initial conditions, and our baryonification expression has a root mean squared error of better than one percent, although this increases on small scales. These errors are comparable to those of previous numerical emulators for these models. Our expressions are enforced to have the physically correct behaviour on large scales and at high redshift. Due to their analytic form, we are able to directly interpret the impact of varying cosmology and feedback parameters, and we can identify parameters which have little to no effect. Each function is based on a different implementation of baryonic physics, and can therefore be used to discriminate between these models when applied to real data. We provide publicly available code for all symbolic approximations found.
rEGGression: an Interactive and Agnostic Tool for the Exploration of Symbolic Regression Models
Jan 29, 2025Abstract:Regression analysis is used for prediction and to understand the effect of independent variables on dependent variables. Symbolic regression (SR) automates the search for non-linear regression models, delivering a set of hypotheses that balances accuracy with the possibility to understand the phenomena. Many SR implementations return a Pareto front allowing the choice of the best trade-off. However, this hides alternatives that are close to non-domination, limiting these choices. Equality graphs (e-graphs) allow to represent large sets of expressions compactly by efficiently handling duplicated parts occurring in multiple expressions. E-graphs allow to store and query all SR solution candidates visited in one or multiple GP runs efficiently and open the possibility to analyse much larger sets of SR solution candidates. We introduce rEGGression, a tool using e-graphs to enable the exploration of a large set of symbolic expressions which provides querying, filtering, and pattern matching features creating an interactive experience to gain insights about SR models. The main highlight is its focus in the exploration of the building blocks found during the search that can help the experts to find insights about the studied phenomena.This is possible by exploiting the pattern matching capability of the e-graph data structure.
Improving Genetic Programming for Symbolic Regression with Equality Graphs
Jan 29, 2025Abstract:The search for symbolic regression models with genetic programming (GP) has a tendency of revisiting expressions in their original or equivalent forms. Repeatedly evaluating equivalent expressions is inefficient, as it does not immediately lead to better solutions. However, evolutionary algorithms require diversity and should allow the accumulation of inactive building blocks that can play an important role at a later point. The equality graph is a data structure capable of compactly storing expressions and their equivalent forms allowing an efficient verification of whether an expression has been visited in any of their stored equivalent forms. We exploit the e-graph to adapt the subtree operators to reduce the chances of revisiting expressions. Our adaptation, called eggp, stores every visited expression in the e-graph, allowing us to filter out from the available selection of subtrees all the combinations that would create already visited expressions. Results show that, for small expressions, this approach improves the performance of a simple GP algorithm to compete with PySR and Operon without increasing computational cost. As a highlight, eggp was capable of reliably delivering short and at the same time accurate models for a selected set of benchmarks from SRBench and a set of real-world datasets.
A Comparison of Recent Algorithms for Symbolic Regression to Genetic Programming
Jun 05, 2024



Abstract:Symbolic regression is a machine learning method with the goal to produce interpretable results. Unlike other machine learning methods such as, e.g. random forests or neural networks, which are opaque, symbolic regression aims to model and map data in a way that can be understood by scientists. Recent advancements, have attempted to bridge the gap between these two fields; new methodologies attempt to fuse the mapping power of neural networks and deep learning techniques with the explanatory power of symbolic regression. In this paper, we examine these new emerging systems and test the performance of an end-to-end transformer model for symbolic regression versus the reigning traditional methods based on genetic programming that have spearheaded symbolic regression throughout the years. We compare these systems on novel datasets to avoid bias to older methods who were improved on well-known benchmark datasets. Our results show that traditional GP methods as implemented e.g., by Operon still remain superior to two recently published symbolic regression methods.
The Inefficiency of Genetic Programming for Symbolic Regression -- Extended Version
Apr 26, 2024



Abstract:We analyse the search behaviour of genetic programming for symbolic regression in practically relevant but limited settings, allowing exhaustive enumeration of all solutions. This enables us to quantify the success probability of finding the best possible expressions, and to compare the search efficiency of genetic programming to random search in the space of semantically unique expressions. This analysis is made possible by improved algorithms for equality saturation, which we use to improve the Exhaustive Symbolic Regression algorithm; this produces the set of semantically unique expression structures, orders of magnitude smaller than the full symbolic regression search space. We compare the efficiency of random search in the set of unique expressions and genetic programming. For our experiments we use two real-world datasets where symbolic regression has been used to produce well-fitting univariate expressions: the Nikuradse dataset of flow in rough pipes and the Radial Acceleration Relation of galaxy dynamics. The results show that genetic programming in such limited settings explores only a small fraction of all unique expressions, and evaluates expressions repeatedly that are congruent to already visited expressions.
A precise symbolic emulator of the linear matter power spectrum
Nov 27, 2023



Abstract:Computing the matter power spectrum, $P(k)$, as a function of cosmological parameters can be prohibitively slow in cosmological analyses, hence emulating this calculation is desirable. Previous analytic approximations are insufficiently accurate for modern applications, so black-box, uninterpretable emulators are often used. We utilise an efficient genetic programming based symbolic regression framework to explore the space of potential mathematical expressions which can approximate the power spectrum and $\sigma_8$. We learn the ratio between an existing low-accuracy fitting function for $P(k)$ and that obtained by solving the Boltzmann equations and thus still incorporate the physics which motivated this earlier approximation. We obtain an analytic approximation to the linear power spectrum with a root mean squared fractional error of 0.2% between $k = 9\times10^{-3} - 9 \, h{\rm \, Mpc^{-1}}$ and across a wide range of cosmological parameters, and we provide physical interpretations for various terms in the expression. We also provide a simple analytic approximation for $\sigma_8$ with a similar accuracy, with a root mean squared fractional error of just 0.4% when evaluated across the same range of cosmologies. This function is easily invertible to obtain $A_{\rm s}$ as a function of $\sigma_8$ and the other cosmological parameters, if preferred. It is possible to obtain symbolic approximations to a seemingly complex function at a precision required for current and future cosmological analyses without resorting to deep-learning techniques, thus avoiding their black-box nature and large number of parameters. Our emulator will be usable long after the codes on which numerical approximations are built become outdated.
Learning Difference Equations with Structured Grammatical Evolution for Postprandial Glycaemia Prediction
Jul 03, 2023



Abstract:People with diabetes must carefully monitor their blood glucose levels, especially after eating. Blood glucose regulation requires a proper combination of food intake and insulin boluses. Glucose prediction is vital to avoid dangerous post-meal complications in treating individuals with diabetes. Although traditional methods, such as artificial neural networks, have shown high accuracy rates, sometimes they are not suitable for developing personalised treatments by physicians due to their lack of interpretability. In this study, we propose a novel glucose prediction method emphasising interpretability: Interpretable Sparse Identification by Grammatical Evolution. Combined with a previous clustering stage, our approach provides finite difference equations to predict postprandial glucose levels up to two hours after meals. We divide the dataset into four-hour segments and perform clustering based on blood glucose values for the twohour window before the meal. Prediction models are trained for each cluster for the two-hour windows after meals, allowing predictions in 15-minute steps, yielding up to eight predictions at different time horizons. Prediction safety was evaluated based on Parkes Error Grid regions. Our technique produces safe predictions through explainable expressions, avoiding zones D (0.2% average) and E (0%) and reducing predictions on zone C (6.2%). In addition, our proposal has slightly better accuracy than other techniques, including sparse identification of non-linear dynamics and artificial neural networks. The results demonstrate that our proposal provides interpretable solutions without sacrificing prediction accuracy, offering a promising approach to glucose prediction in diabetes management that balances accuracy, interpretability, and computational efficiency.
Steel Phase Kinetics Modeling using Symbolic Regression
Dec 19, 2022


Abstract:We describe an approach for empirical modeling of steel phase kinetics based on symbolic regression and genetic programming. The algorithm takes processed data gathered from dilatometer measurements and produces a system of differential equations that models the phase kinetics. Our initial results demonstrate that the proposed approach allows to identify compact differential equations that fit the data. The model predicts ferrite, pearlite and bainite formation for a single steel type. Martensite is not yet included in the model. Future work shall incorporate martensite and generalize to multiple steel types with different chemical compositions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge