Michael Frank
Improving Energy Efficiency in Manufacturing: A Novel Expert System Shell
Nov 02, 2024Abstract:Expert systems are effective tools for automatically identifying energy efficiency potentials in manufacturing, thereby contributing significantly to global climate targets. These systems analyze energy data, pinpoint inefficiencies, and recommend optimizations to reduce energy consumption. Beyond systematic approaches for developing expert systems, there is a pressing need for simple and rapid software implementation solutions. Expert system shells, which facilitate the swift development and deployment of expert systems, are crucial tools in this process. They provide a template that simplifies the creation and integration of expert systems into existing manufacturing processes. This paper provides a comprehensive comparison of existing expert system shells regarding their suitability for improving energy efficiency, highlighting significant gaps and limitations. To address these deficiencies, we introduce a novel expert system shell, implemented in Jupyter Notebook, that provides a flexible and easily integrable solution for expert system development.
A systematic review on expert systems for improving energy efficiency in the manufacturing industry
Jul 05, 2024Abstract:Against the backdrop of the European Union's commitment to achieve climate neutrality by 2050, efforts to improve energy efficiency are being intensified. The manufacturing industry is a key focal point of these endeavors due to its high final electrical energy demand, while simultaneously facing a growing shortage of skilled workers crucial for meeting established goals. Expert systems (ESs) offer the chance to overcome this challenge by automatically identifying potential energy efficiency improvements and thereby playing a significant role in reducing electricity consumption. This paper systematically reviews state-of-the-art approaches of ESs aimed at improving energy efficiency in industry, with a focus on manufacturing. The literature search yields 1692 results, of which 54 articles published between 1987 and 2023 are analyzed in depth. These publications are classified according to the system boundary, manufacturing type, application perspective, application purpose, ES type, and industry. Furthermore, we examine the structure, implementation, utilization, and development of ESs in this context. Through this analysis, the review reveals research gaps, pointing toward promising topics for future research.
Neural scaling laws for phenotypic drug discovery
Sep 28, 2023



Abstract:Recent breakthroughs by deep neural networks (DNNs) in natural language processing (NLP) and computer vision have been driven by a scale-up of models and data rather than the discovery of novel computing paradigms. Here, we investigate if scale can have a similar impact for models designed to aid small molecule drug discovery. We address this question through a large-scale and systematic analysis of how DNN size, data diet, and learning routines interact to impact accuracy on our Phenotypic Chemistry Arena (Pheno-CA) benchmark: a diverse set of drug development tasks posed on image-based high content screening data. Surprisingly, we find that DNNs explicitly supervised to solve tasks in the Pheno-CA do not continuously improve as their data and model size is scaled-up. To address this issue, we introduce a novel precursor task, the Inverse Biological Process (IBP), which is designed to resemble the causal objective functions that have proven successful for NLP. We indeed find that DNNs first trained with IBP then probed for performance on the Pheno-CA significantly outperform task-supervised DNNs. More importantly, the performance of these IBP-trained DNNs monotonically improves with data and model scale. Our findings reveal that the DNN ingredients needed to accurately solve small molecule drug development tasks are already in our hands, and project how much more experimental data is needed to achieve any desired level of improvement. We release our Pheno-CA benchmark and code to encourage further study of neural scaling laws for small molecule drug discovery.
Tensor Slicing and Optimization for Multicore NPUs
Apr 06, 2023Abstract:Although code generation for Convolution Neural Network (CNN) models has been extensively studied, performing efficient data slicing and parallelization for highly-constrai\-ned Multicore Neural Processor Units (NPUs) is still a challenging problem. Given the size of convolutions' input/output tensors and the small footprint of NPU on-chip memories, minimizing memory transactions while maximizing parallelism and MAC utilization are central to any effective solution. This paper proposes a TensorFlow XLA/LLVM compiler optimization pass for Multicore NPUs, called Tensor Slicing Optimization (TSO), which: (a) maximizes convolution parallelism and memory usage across NPU cores; and (b) reduces data transfers between host and NPU on-chip memories by using DRAM memory burst time estimates to guide tensor slicing. To evaluate the proposed approach, a set of experiments was performed using the NeuroMorphic Processor (NMP), a multicore NPU containing 32 RISC-V cores extended with novel CNN instructions. Experimental results show that TSO is capable of identifying the best tensor slicing that minimizes execution time for a set of CNN models. Speed-ups of up to 21.7\% result when comparing the TSO burst-based technique to a no-burst data slicing approach. To validate the generality of the TSO approach, the algorithm was also ported to the Glow Machine Learning framework. The performance of the models were measured on both Glow and TensorFlow XLA/LLVM compilers, revealing similar results.
Acoustically-Driven Phoneme Removal That Preserves Vocal Affect Cues
Oct 26, 2022Abstract:In this paper, we propose a method for removing linguistic information from speech for the purpose of isolating paralinguistic indicators of affect. The immediate utility of this method lies in clinical tests of sensitivity to vocal affect that are not confounded by language, which is impaired in a variety of clinical populations. The method is based on simultaneous recordings of speech audio and electroglottographic (EGG) signals. The speech audio signal is used to estimate the average vocal tract filter response and amplitude envelop. The EGG signal supplies a direct correlate of voice source activity that is mostly independent of phonetic articulation. These signals are used to create a third signal designed to capture as much paralinguistic information from the vocal production system as possible -- maximizing the retention of bioacoustic cues to affect -- while eliminating phonetic cues to verbal meaning. To evaluate the success of this method, we studied the perception of corresponding speech audio and transformed EGG signals in an affect rating experiment with online listeners. The results show a high degree of similarity in the perceived affect of matched signals, indicating that our method is effective.
Computing the Ramsey Number R(4,3,3) using Abstraction and Symmetry breaking
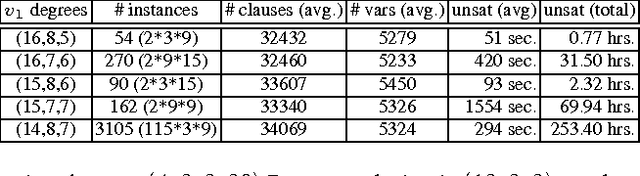
Nov 01, 2015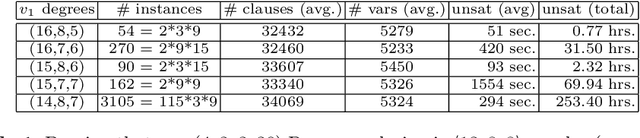


Abstract:The number $R(4,3,3)$ is often presented as the unknown Ramsey number with the best chances of being found "soon". Yet, its precise value has remained unknown for almost 50 years. This paper presents a methodology based on \emph{abstraction} and \emph{symmetry breaking} that applies to solve hard graph edge-coloring problems. The utility of this methodology is demonstrated by using it to compute the value $R(4,3,3)=30$. Along the way it is required to first compute the previously unknown set ${\cal R}(3,3,3;13)$ consisting of 78{,}892 Ramsey colorings.
Solving Graph Coloring Problems with Abstraction and Symmetry
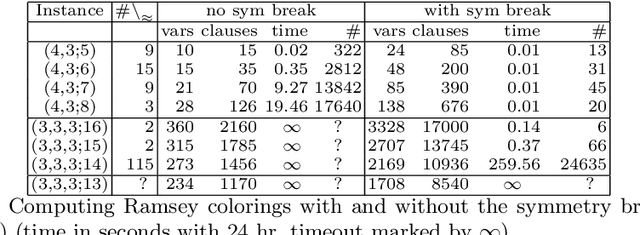
Mar 26, 2015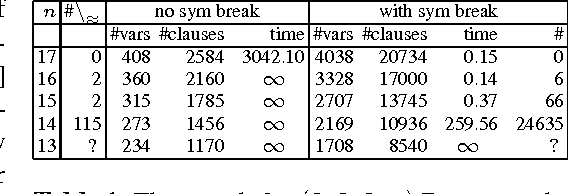


Abstract:This paper introduces a general methodology, based on abstraction and symmetry, that applies to solve hard graph edge-coloring problems and demonstrates its use to provide further evidence that the Ramsey number $R(4,3,3)=30$. The number $R(4,3,3)$ is often presented as the unknown Ramsey number with the best chances of being found "soon". Yet, its precise value has remained unknown for more than 50 years. We illustrate our approach by showing that: (1) there are precisely 78{,}892 $(3,3,3;13)$ Ramsey colorings; and (2) if there exists a $(4,3,3;30)$ Ramsey coloring then it is (13,8,8) regular. Specifically each node has 13 edges in the first color, 8 in the second, and 8 in the third. We conjecture that these two results will help provide a proof that no $(4,3,3;30)$ Ramsey coloring exists implying that $R(4,3,3)=30$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge