Sequential parametrized motion planning and its complexity, II

This is a continuation of our recent paper in which we developed the theory of sequential parametrized motion planning. A sequential parametrized motion planning algorithm produced a motion of the system which is required to visit a prescribed sequence of states, in a certain order, at specified moments of time. In the previous publication we analysed the sequential parametrized topological complexity of the Fadell - Neuwirth fibration which in relevant to the problem of moving multiple robots avoiding collisions with other robots and with obstacles in the Euclidean space. Besides, in the preceeding paper we found the sequential parametrised topological complexity of the Fadell - Neuwirth bundle for the case of the Euclidean space $\Bbb R^d$ of odd dimension as well as the case $d=2$. In the present paper we give the complete answer for an arbitrary $d\ge 2$ even. Moreover, we present an explicit motion planning algorithm for controlling multiple robots in $\Bbb R^d$ having the minimal possible topological complexity; this algorithm is applicable to any number $n$ of robots and any number $m\ge 2$ of obstacles.

Parametrized motion planning and topological complexity

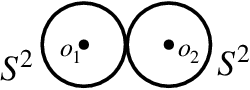
In this paper we study paramertized motion planning algorithms which provide universal and flexible solutions to diverse motion planning problems. Such algorithms are intended to function under a variety of external conditions which are viewed as parameters and serve as part of the input of the algorithm. Continuing a recent paper, we study further the concept of parametrized topological complexity. We analyse in full detail the problem of controlling a swarm of robots in the presence of multiple obstacles in Euclidean space which served for us a natural motivating example. We present an explicit parametrized motion planning algorithm solving the motion planning problem for any number of robots and obstacles.. This algorithm is optimal, it has minimal possible topological complexity for any d odd. Besides, we describe a modification of this algorithm which is optimal for d even. We also analyse the parametrized topological complexity of sphere bundles using the Stiefel - Whitney characteristic classes.

Parametrized topological complexity of collision-free motion planning in the plane

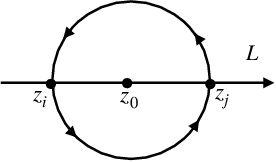
Parametrized motion planning algorithms have high degrees of universality and flexibility, as they are designed to work under a variety of external conditions, which are viewed as parameters and form part of the input of the underlying motion planning problem. In this paper, we analyze the parameterized motion planning problem for the motion of many distinct points in the plane, moving without collision and avoiding multiple distinct obstacles with a priori unknown positions. This complements our prior work [arXiv:2009.06023], where parameterized motion planning algorithms were introduced, and the obstacle-avoiding collision-free motion planning problem in three-dimensional space was fully investigated. The planar case requires different algebraic and topological tools than its spatial analog.

Topological Robotics: Subspace Arrangements and Collision Free Motion Planning

We study an elementary problem of the topological robotics: collective motion of a set of $n$ distinct particles which one has to move from an initial configuration to a final configuration, with the requirement that no collisions occur in the process of motion. The ultimate goal is to construct an algorithm which will perform this task once the initial and the final configurations are given. This reduces to a topological problem of finding the topological complexity TC(C_n(\R^m)) of the configutation space C_n(\R^m) of $n$ distinct ordered particles in \R^m. We solve this problem for m=2 (the planar case) and for all odd m, including the case m=3 (particles in the three-dimensional space). We also study a more general motion planning problem in Euclidean space with a hyperplane arrangement as obstacle.

Topological robotics: motion planning in projective spaces

We study an elementary problem of topological robotics: rotation of a line, which is fixed by a revolving joint at a base point: one wants to bring the line from its initial position to a final position by a continuous motion in the space. The final goal is to construct an algorithm which will perform this task once the initial and final positions are given. Any such motion planning algorithm will have instabilities, which are caused by topological reasons. A general approach to study instabilities of robot motion was suggested recently by the first named author. With any path-connected topological space X one associates a number TC(X), called the topological complexity of X. This number is of fundamental importance for the motion planning problem: TC(X) determines character of instabilities which have all motion planning algorithms in X. In the present paper we study the topological complexity of real projective spaces. In particular we compute TC(RP^n) for all n<24. Our main result is that (for n distinct from 1, 3, 7) the problem of calculating of TC(RP^n) is equivalent to finding the smallest k such that RP^n can be immersed into the Euclidean space R^{k-1}.

Instabilities of Robot Motion

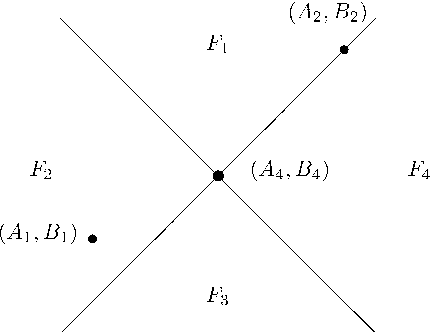
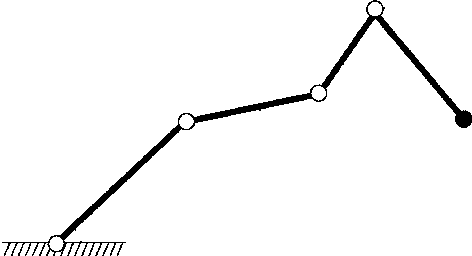
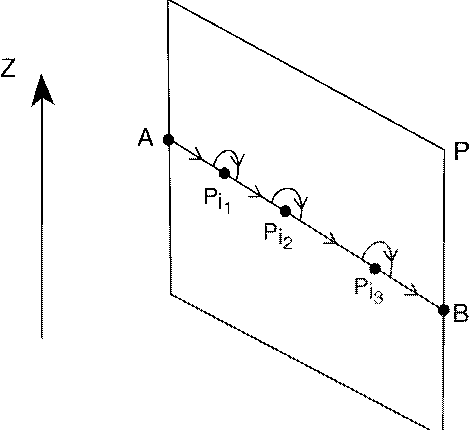
Instabilities of robot motion are caused by topological reasons. In this paper we find a relation between the topological properties of a configuration space (the structure of its cohomology algebra) and the character of instabilities, which are unavoidable in any motion planning algorithm. More specifically, let $X$ denote the space of all admissible configurations of a mechanical system. A {\it motion planner} is given by a splitting $X\times X = F_1\cup F_2\cup ... \cup F_k$ (where $F_1, ..., F_k$ are pairwise disjoint ENRs, see below) and by continuous maps $s_j: F_j \to PX,$ such that $E\circ s_j =1_{F_j}$. Here $PX$ denotes the space of all continuous paths in $X$ (admissible motions of the system) and $E: PX\to X\times X$ denotes the map which assigns to a path the pair of its initial -- end points. Any motion planner determines an algorithm of motion planning for the system. In this paper we apply methods of algebraic topology to study the minimal number of sets $F_j$ in any motion planner in $X$. We also introduce a new notion of {\it order of instability} of a motion planner; it describes the number of essentially distinct motions which may occur as a result of small perturbations of the input data. We find the minimal order of instability, which may have motion planners on a given configuration space $X$. We study a number of specific problems: motion of a rigid body in $\R^3$, a robot arm, motion in $\R^3$ in the presence of obstacles, and others.