Learning Compositional Rules via Neural Program Synthesis

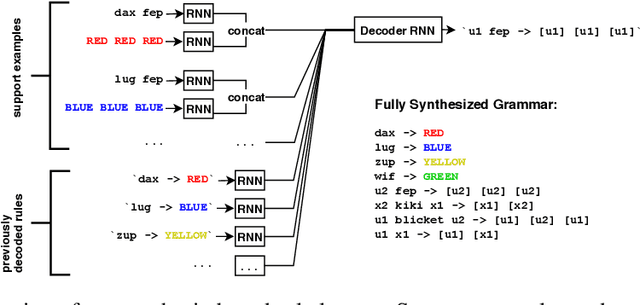
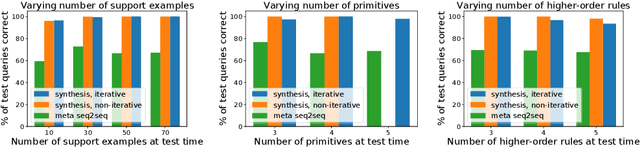
Many aspects of human reasoning, including language, require learning rules from very little data. Humans can do this, often learning systematic rules from very few examples, and combining these rules to form compositional rule-based systems. Current neural architectures, on the other hand, often fail to generalize in a compositional manner, especially when evaluated in ways that vary systematically from training. In this work, we present a neuro-symbolic model which learns entire rule systems from a small set of examples. Instead of directly predicting outputs from inputs, we train our model to induce the explicit system of rules governing a set of previously seen examples, drawing upon techniques from the neural program synthesis literature. Our rule-synthesis approach outperforms neural meta-learning techniques in three domains: an artificial instruction-learning domain used to evaluate human learning, the SCAN challenge datasets, and learning rule-based translations of number words into integers for a wide range of human languages.

The Variational Homoencoder: Learning to learn high capacity generative models from few examples

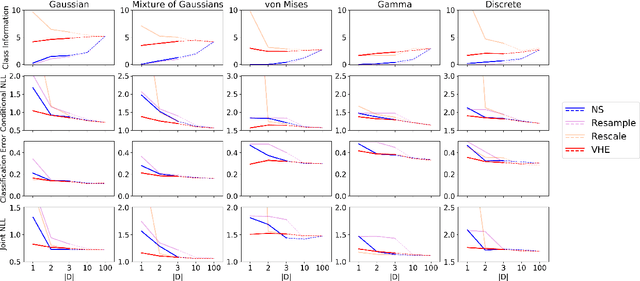
Hierarchical Bayesian methods can unify many related tasks (e.g. k-shot classification, conditional and unconditional generation) as inference within a single generative model. However, when this generative model is expressed as a powerful neural network such as a PixelCNN, we show that existing learning techniques typically fail to effectively use latent variables. To address this, we develop a modification of the Variational Autoencoder in which encoded observations are decoded to new elements from the same class. This technique, which we call a Variational Homoencoder (VHE), produces a hierarchical latent variable model which better utilises latent variables. We use the VHE framework to learn a hierarchical PixelCNN on the Omniglot dataset, which outperforms all existing models on test set likelihood and achieves strong performance on one-shot generation and classification tasks. We additionally validate the VHE on natural images from the YouTube Faces database. Finally, we develop extensions of the model that apply to richer dataset structures such as factorial and hierarchical categories.