Machine Learning for Discovering Effective Interaction Kernels between Celestial Bodies from Ephemerides

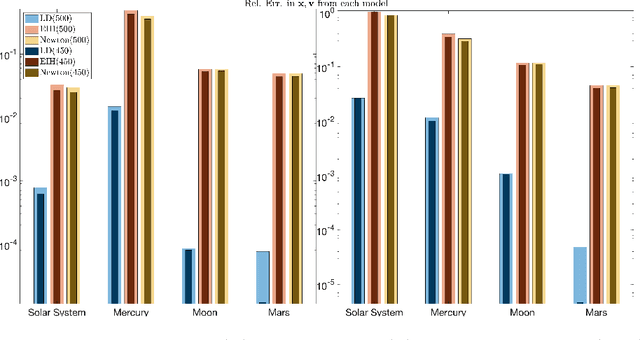
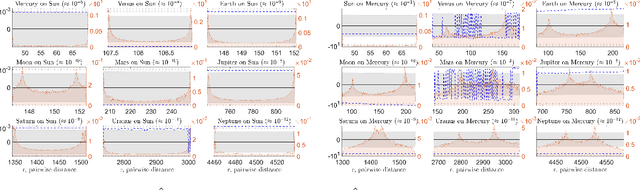
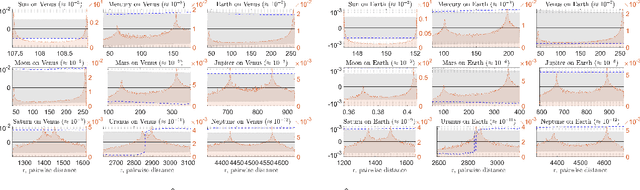
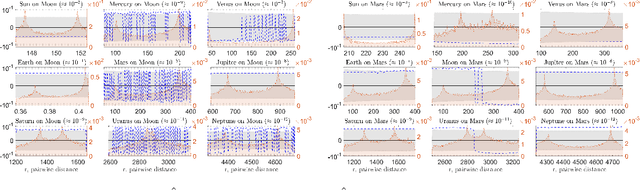
Building accurate and predictive models of the underlying mechanisms of celestial motion has inspired fundamental developments in theoretical physics. Candidate theories seek to explain observations and predict future positions of planets, stars, and other astronomical bodies as faithfully as possible. We use a data-driven learning approach, extending that developed in Lu et al. ($2019$) and extended in Zhong et al. ($2020$), to a derive stable and accurate model for the motion of celestial bodies in our Solar System. Our model is based on a collective dynamics framework, and is learned from the NASA Jet Propulsion Lab's development ephemerides. By modeling the major astronomical bodies in the Solar System as pairwise interacting agents, our learned model generate extremely accurate dynamics that preserve not only intrinsic geometric properties of the orbits, but also highly sensitive features of the dynamics, such as perihelion precession rates. Our learned model can provide a unified explanation to the observation data, especially in terms of reproducing the perihelion precession of Mars, Mercury, and the Moon. Moreover, Our model outperforms Newton's Law of Universal Gravitation in all cases and performs similarly to, and exceeds on the Moon, the Einstein-Infeld-Hoffman equations derived from Einstein's theory of general relativity.

Nonlinear model reduction for slow-fast stochastic systems near manifolds

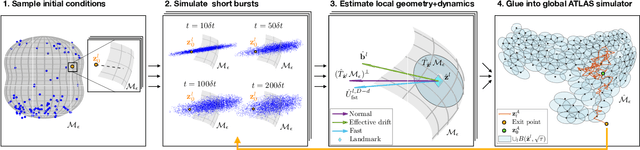
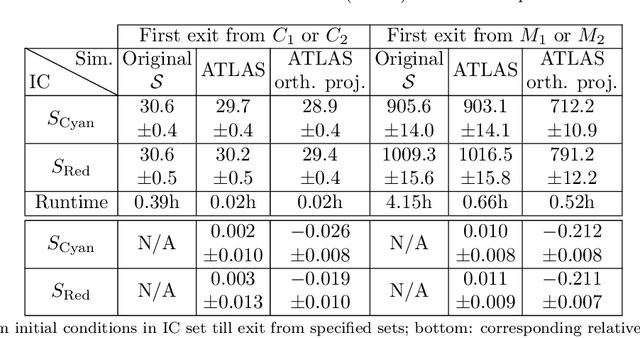
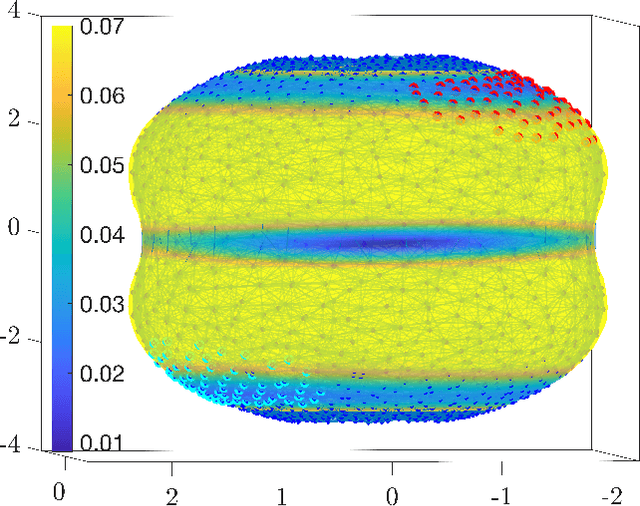
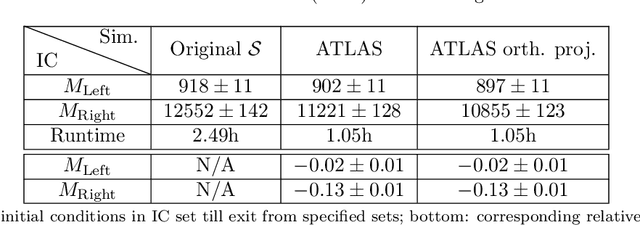
We introduce a nonlinear stochastic model reduction technique for high-dimensional stochastic dynamical systems that have a low-dimensional invariant effective manifold with slow dynamics, and high-dimensional, large fast modes. Given only access to a black box simulator from which short bursts of simulation can be obtained, we estimate the invariant manifold, a process of the effective (stochastic) dynamics on it, and construct an efficient simulator thereof. These estimation steps can be performed on-the-fly, leading to efficient exploration of the effective state space, without losing consistency with the underlying dynamics. This construction enables fast and efficient simulation of paths of the effective dynamics, together with estimation of crucial features and observables of such dynamics, including the stationary distribution, identification of metastable states, and residence times and transition rates between them.

Learning Interaction Kernels for Agent Systems on Riemannian Manifolds

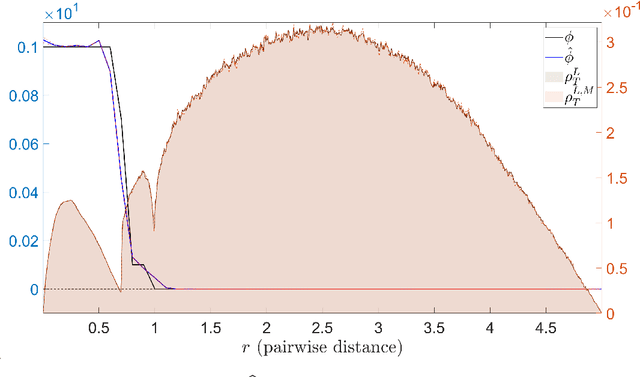
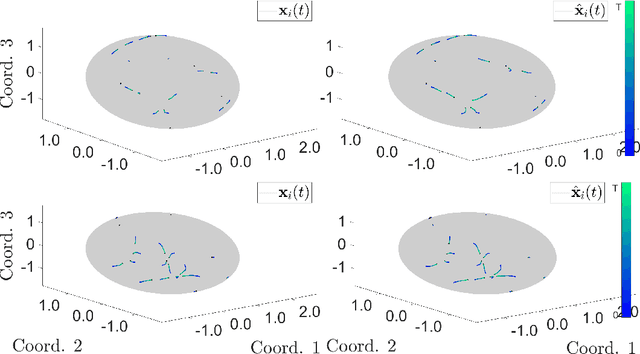
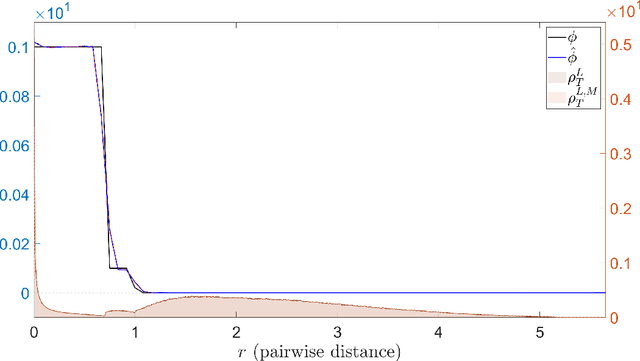
Interacting agent and particle systems are extensively used to model complex phenomena in science and engineering. We consider the problem of learning interaction kernels in these dynamical systems constrained to evolve on Riemannian manifolds from given trajectory data. The models we consider are based on interaction kernels depending on pairwise Riemannian distances between agents, with agents interacting locally along the direction of the shortest geodesic connecting them. We show that our estimators converge at a rate that is independent of the dimension of the state space, and derive bounds on the trajectory estimation error, on the manifold, between the observed and estimated dynamics. We demonstrate the performance of our estimator on two classical first order interacting systems: Opinion Dynamics and a Predator-Swarm system, with each system constrained on two prototypical manifolds, the $2$-dimensional sphere and the Poincar\'e disk model of hyperbolic space.

Multiscale regression on unknown manifolds

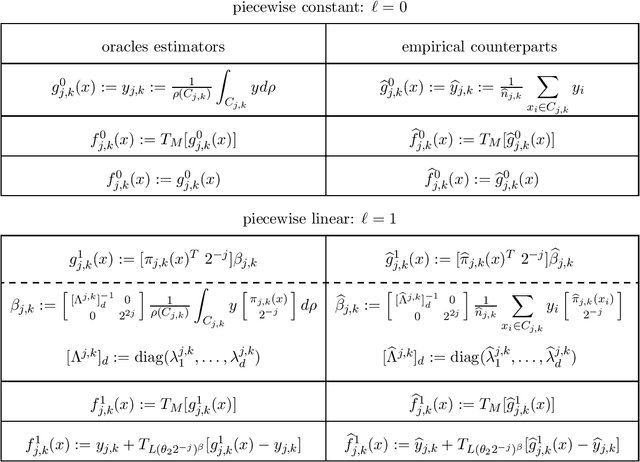
We consider the regression problem of estimating functions on $\mathbb{R}^D$ but supported on a $d$-dimensional manifold $ \mathcal{M} \subset \mathbb{R}^D $ with $ d \ll D $. Drawing ideas from multi-resolution analysis and nonlinear approximation, we construct low-dimensional coordinates on $\mathcal{M}$ at multiple scales, and perform multiscale regression by local polynomial fitting. We propose a data-driven wavelet thresholding scheme that automatically adapts to the unknown regularity of the function, allowing for efficient estimation of functions exhibiting nonuniform regularity at different locations and scales. We analyze the generalization error of our method by proving finite sample bounds in high probability on rich classes of priors. Our estimator attains optimal learning rates (up to logarithmic factors) as if the function was defined on a known Euclidean domain of dimension $d$, instead of an unknown manifold embedded in $\mathbb{R}^D$. The implemented algorithm has quasilinear complexity in the sample size, with constants linear in $D$ and exponential in $d$. Our work therefore establishes a new framework for regression on low-dimensional sets embedded in high dimensions, with fast implementation and strong theoretical guarantees.

Anatomically-Informed Deep Learning on Contrast-Enhanced Cardiac MRI for Scar Segmentation and Clinical Feature Extraction

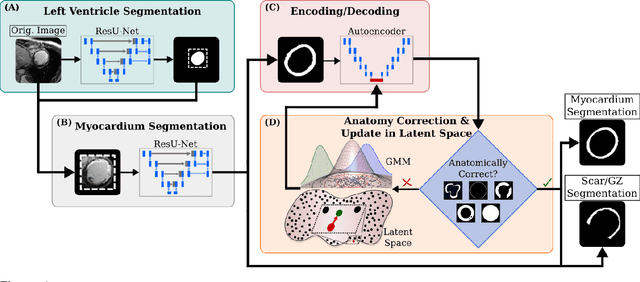
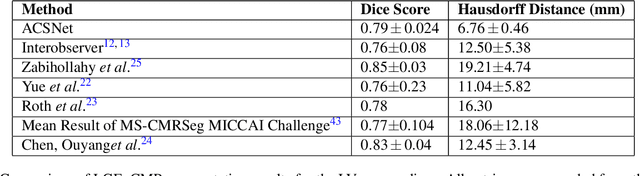
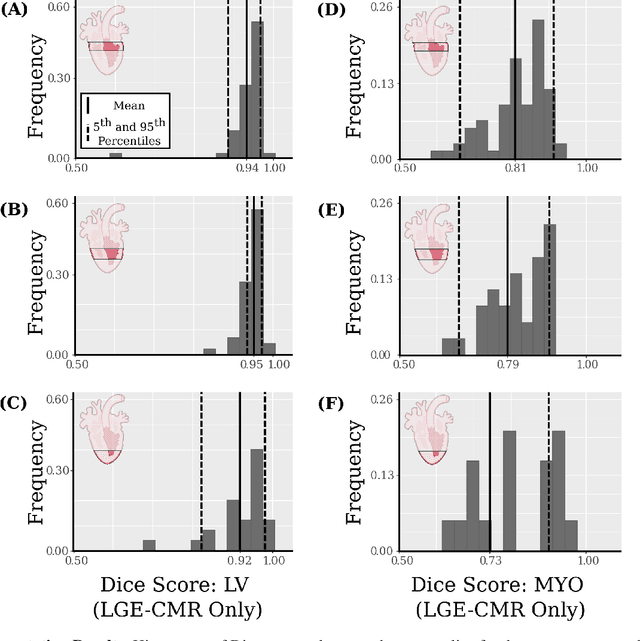
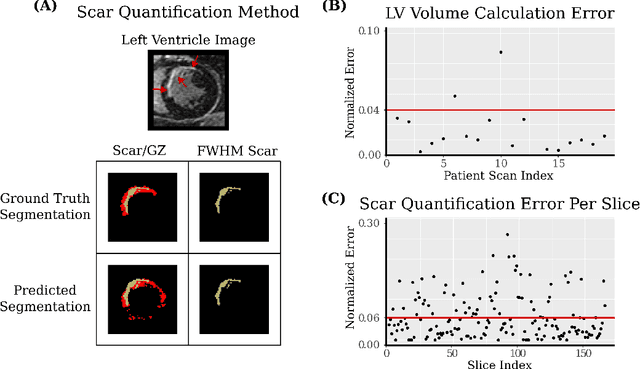
Many cardiac diseases are associated with structural remodeling of the myocardium. Cardiac magnetic resonance (CMR) imaging with contrast enhancement, such as late gadolinium enhancement (LGE), has unparalleled capability to visualize fibrotic tissue remodeling, allowing for direct characterization of the pathophysiological abnormalities leading to arrhythmias and sudden cardiac death (SCD). Automating segmentation of the ventricles with fibrosis distribution could dramatically enhance the utility of LGE-CMR in heart disease clinical research and in the management of patients with risk of arrhythmias and SCD. Here we describe an anatomically-informed deep learning (DL) approach to myocardium and scar segmentation and clinical feature extraction from LGE-CMR images. The technology enables clinical use by ensuring anatomical accuracy and complete automation. Algorithm performance is strong for both myocardium segmentation ($98\%$ accuracy and $0.79$ Dice score in a hold-out test set) and evaluation measures shown to correlate with heart disease, such as scar amount ($6.3\%$ relative error). Our approach for clinical feature extraction, which satisfies highly complex geometric constraints without stunting the learning process, has the potential of a broad applicability in computer vision beyond cardiology, and even outside of medicine.

Learning Theory for Inferring Interaction Kernels in Second-Order Interacting Agent Systems

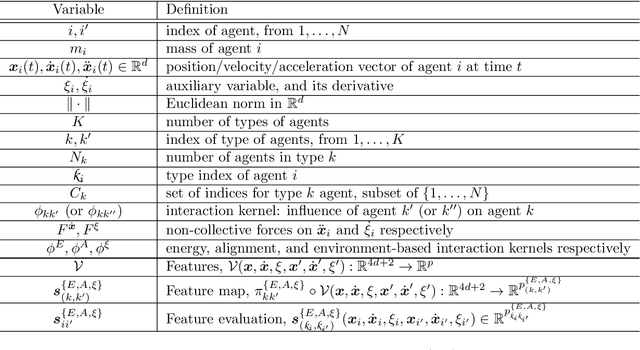
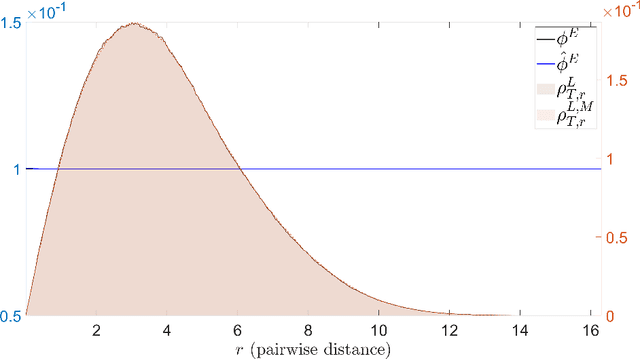
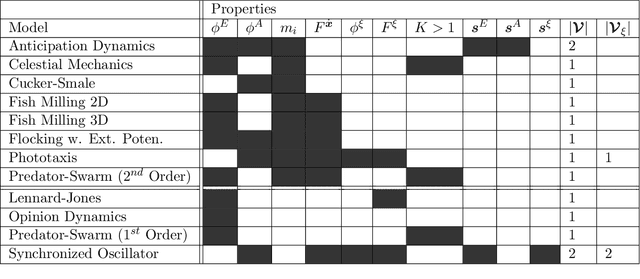
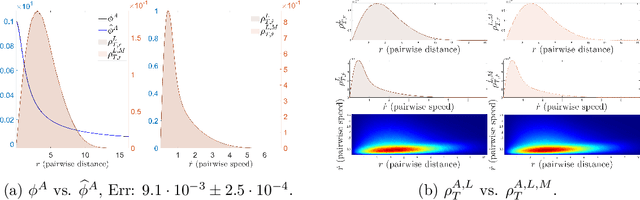
Modeling the complex interactions of systems of particles or agents is a fundamental scientific and mathematical problem that is studied in diverse fields, ranging from physics and biology, to economics and machine learning. In this work, we describe a very general second-order, heterogeneous, multivariable, interacting agent model, with an environment, that encompasses a wide variety of known systems. We describe an inference framework that uses nonparametric regression and approximation theory based techniques to efficiently derive estimators of the interaction kernels which drive these dynamical systems. We develop a complete learning theory which establishes strong consistency and optimal nonparametric min-max rates of convergence for the estimators, as well as provably accurate predicted trajectories. The estimators exploit the structure of the equations in order to overcome the curse of dimensionality and we describe a fundamental coercivity condition on the inverse problem which ensures that the kernels can be learned and relates to the minimal singular value of the learning matrix. The numerical algorithm presented to build the estimators is parallelizable, performs well on high-dimensional problems, and is demonstrated on complex dynamical systems.

Learning interaction kernels in stochastic systems of interacting particles from multiple trajectories

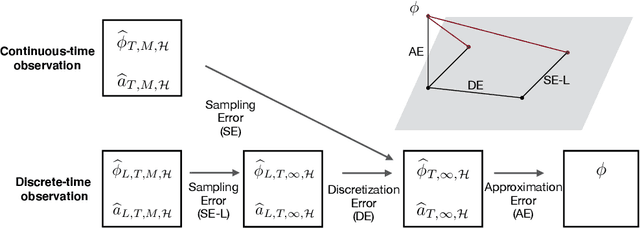
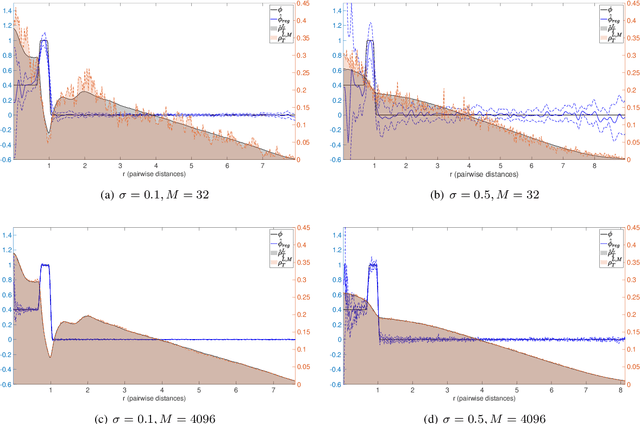
We consider stochastic systems of interacting particles or agents, with dynamics determined by an interaction kernel which only depends on pairwise distances. We study the problem of inferring this interaction kernel from observations of the positions of the particles, in either continuous or discrete time, along multiple independent trajectories. We introduce a nonparametric inference approach to this inverse problem, based on a regularized maximum likelihood estimator constrained to suitable hypothesis spaces adaptive to data. We show that a coercivity condition enables us to control the condition number of this problem and prove the consistency of our estimator, and that in fact it converges at a near-optimal learning rate, equal to the min-max rate of $1$-dimensional non-parametric regression. In particular, this rate is independent of the dimension of the state space, which is typically very high. We also analyze the discretization errors in the case of discrete-time observations, showing that it is of order $1/2$ in terms of the time gaps between observations. This term, when large, dominates the sampling error and the approximation error, preventing convergence of the estimator. Finally, we exhibit an efficient parallel algorithm to construct the estimator from data, and we demonstrate the effectiveness of our algorithm with numerical tests on prototype systems including stochastic opinion dynamics and a Lennard-Jones model.

Data-driven Discovery of Emergent Behaviors in Collective Dynamics

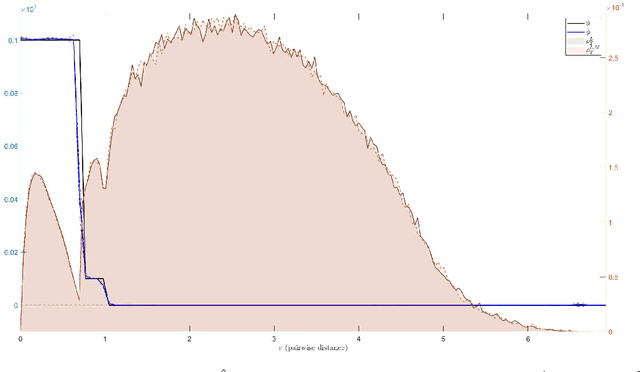
Particle- and agent-based systems are a ubiquitous modeling tool in many disciplines. We consider the fundamental problem of inferring interaction kernels from observations of agent-based dynamical systems given observations of trajectories, in particular for collective dynamical systems exhibiting emergent behaviors with complicated interaction kernels, in a nonparametric fashion, and for kernels which are parametrized by a single unknown parameter. We extend the estimators introduced in \cite{PNASLU}, which are based on suitably regularized least squares estimators, to these larger classes of systems. We provide extensive numerical evidence that the estimators provide faithful approximations to the interaction kernels, and provide accurate predictions for trajectories started at new initial conditions, both throughout the ``training'' time interval in which the observations were made, and often much beyond. We demonstrate these features on prototypical systems displaying collective behaviors, ranging from opinion dynamics, flocking dynamics, self-propelling particle dynamics, synchronized oscillator dynamics, and a gravitational system. Our experiments also suggest that our estimated systems can display the same emergent behaviors of the observed systems, that occur at larger timescales than those used in the training data. Finally, in the case of families of systems governed by a parameterized family of interaction kernels, we introduce novel estimators that estimate the parameterized family of kernels, splitting it into a common interaction kernel and the action of parameters. We demonstrate this in the case of gravity, by learning both the ``common component'' $1/r^2$ and the dependency on mass, without any a priori knowledge of either one, from observations of planetary motions in our solar system.

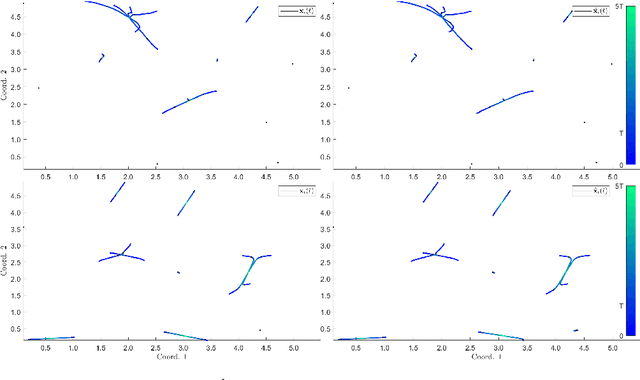
Learning interaction kernels in heterogeneous systems of agents from multiple trajectories

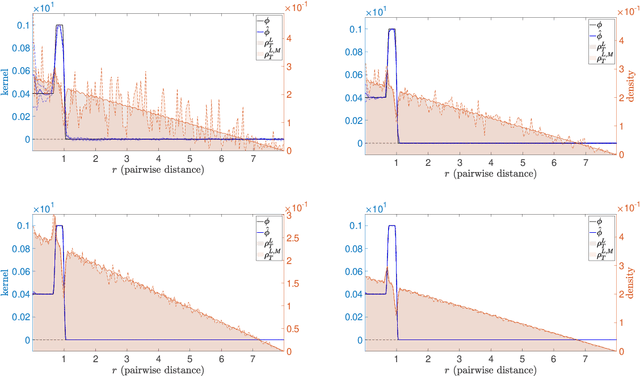
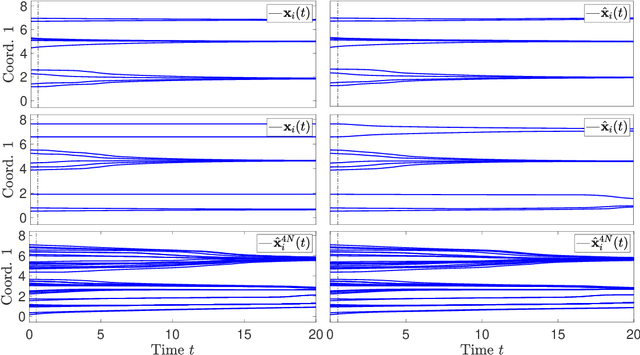
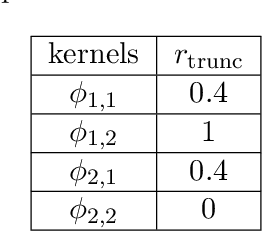
Systems of interacting particles or agents have wide applications in many disciplines such as Physics, Chemistry, Biology and Economics. These systems are governed by interaction laws, which are often unknown: estimating them from observation data is a fundamental task that can provide meaningful insights and accurate predictions of the behaviour of the agents. In this paper, we consider the inverse problem of learning interaction laws given data from multiple trajectories, in a nonparametric fashion, when the interaction kernels depend on pairwise distances. We establish a condition for learnability of interaction kernels, and construct estimators that are guaranteed to converge in a suitable $L^2$ space, at the optimal min-max rate for 1-dimensional nonparametric regression. We propose an efficient learning algorithm based on least squares, which can be implemented in parallel for multiple trajectories and is therefore well-suited for the high dimensional, big data regime. Numerical simulations on a variety examples, including opinion dynamics, predator-swarm dynamics and heterogeneous particle dynamics, suggest that the learnability condition is satisfied in models used in practice, and the rate of convergence of our estimator is consistent with the theory. These simulations also suggest that our estimators are robust to noise in the observations, and produce accurate predictions of dynamics in relative large time intervals, even when they are learned from data collected in short time intervals.

Learning by Active Nonlinear Diffusion

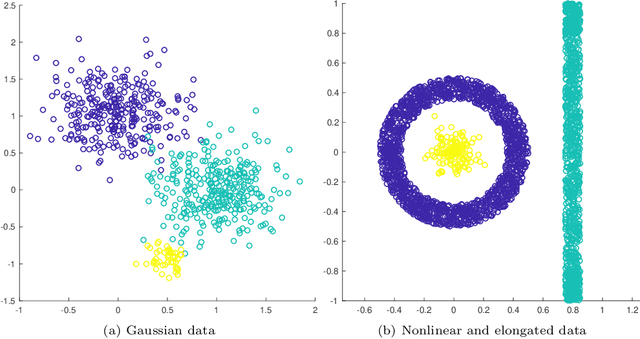
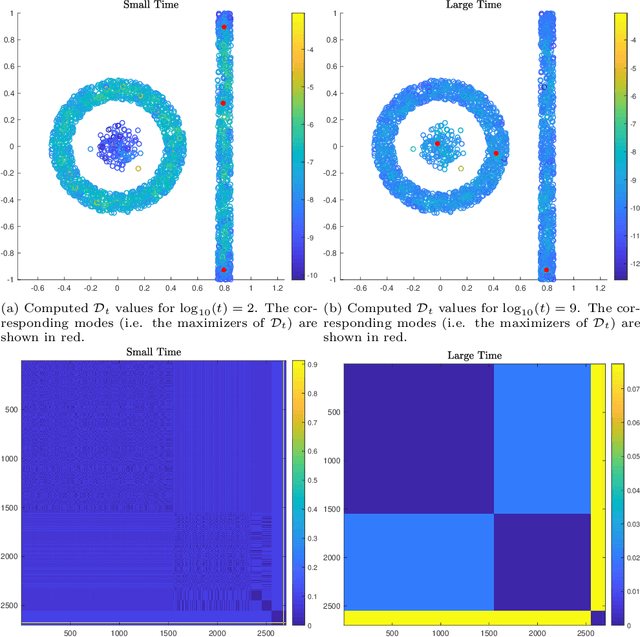
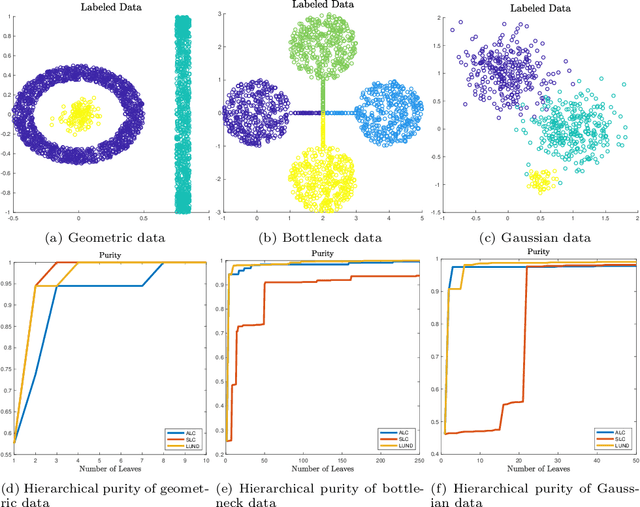
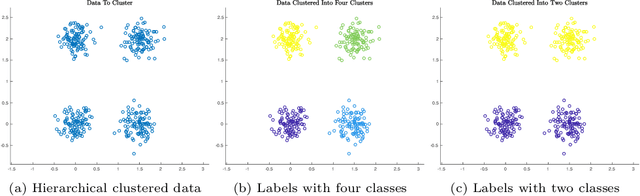
This article proposes an active learning method for high dimensional data, based on intrinsic data geometries learned through diffusion processes on graphs. Diffusion distances are used to parametrize low-dimensional structures on the dataset, which allow for high-accuracy labelings of the dataset with only a small number of carefully chosen labels. The geometric structure of the data suggests regions that have homogeneous labels, as well as regions with high label complexity that should be queried for labels. The proposed method enjoys theoretical performance guarantees on a general geometric data model, in which clusters corresponding to semantically meaningful classes are permitted to have nonlinear geometries, high ambient dimensionality, and suffer from significant noise and outlier corruption. The proposed algorithm is implemented in a manner that is quasilinear in the number of unlabeled data points, and exhibits competitive empirical performance on synthetic datasets and real hyperspectral remote sensing images.