Near Optimal Exploration-Exploitation in Non-Communicating Markov Decision Processes

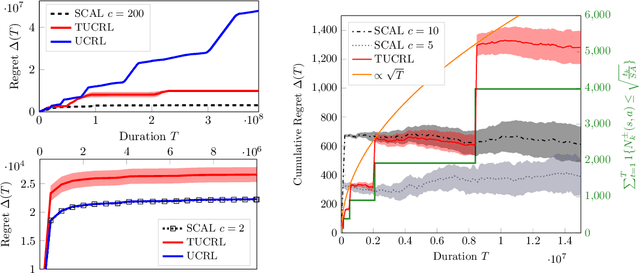
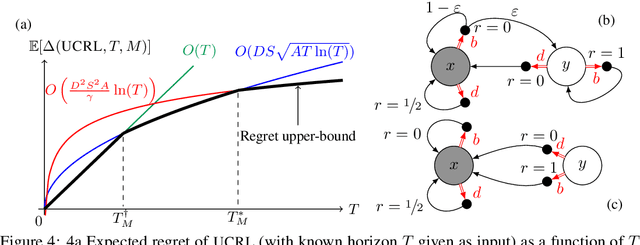
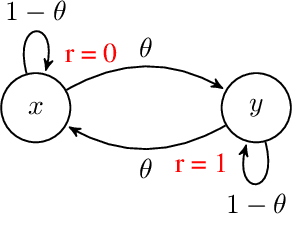
While designing the state space of an MDP, it is common to include states that are transient or not reachable by any policy (e.g., in mountain car, the product space of speed and position contains configurations that are not physically reachable). This leads to defining weakly-communicating or multi-chain MDPs. In this paper, we introduce \tucrl, the first algorithm able to perform efficient exploration-exploitation in any finite Markov Decision Process (MDP) without requiring any form of prior knowledge. In particular, for any MDP with $S^{\texttt{C}}$ communicating states, $A$ actions and $\Gamma^{\texttt{C}} \leq S^{\texttt{C}}$ possible communicating next states, we derive a $\widetilde{O}(D^{\texttt{C}} \sqrt{\Gamma^{\texttt{C}} S^{\texttt{C}} AT})$ regret bound, where $D^{\texttt{C}}$ is the diameter (i.e., the longest shortest path) of the communicating part of the MDP. This is in contrast with optimistic algorithms (e.g., UCRL, Optimistic PSRL) that suffer linear regret in weakly-communicating MDPs, as well as posterior sampling or regularised algorithms (e.g., REGAL), which require prior knowledge on the bias span of the optimal policy to bias the exploration to achieve sub-linear regret. We also prove that in weakly-communicating MDPs, no algorithm can ever achieve a logarithmic growth of the regret without first suffering a linear regret for a number of steps that is exponential in the parameters of the MDP. Finally, we report numerical simulations supporting our theoretical findings and showing how TUCRL overcomes the limitations of the state-of-the-art.

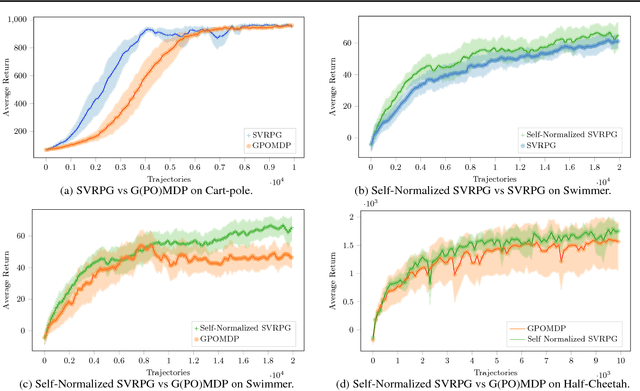
Stochastic Variance-Reduced Policy Gradient

In this paper, we propose a novel reinforcement- learning algorithm consisting in a stochastic variance-reduced version of policy gradient for solving Markov Decision Processes (MDPs). Stochastic variance-reduced gradient (SVRG) methods have proven to be very successful in supervised learning. However, their adaptation to policy gradient is not straightforward and needs to account for I) a non-concave objective func- tion; II) approximations in the full gradient com- putation; and III) a non-stationary sampling pro- cess. The result is SVRPG, a stochastic variance- reduced policy gradient algorithm that leverages on importance weights to preserve the unbiased- ness of the gradient estimate. Under standard as- sumptions on the MDP, we provide convergence guarantees for SVRPG with a convergence rate that is linear under increasing batch sizes. Finally, we suggest practical variants of SVRPG, and we empirically evaluate them on continuous MDPs.

Importance Weighted Transfer of Samples in Reinforcement Learning

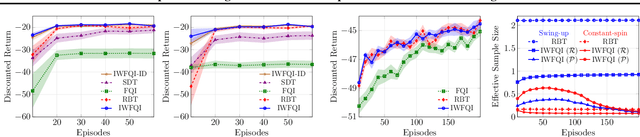
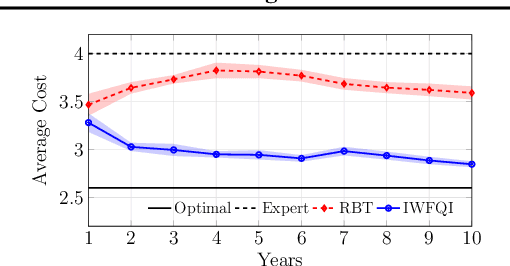
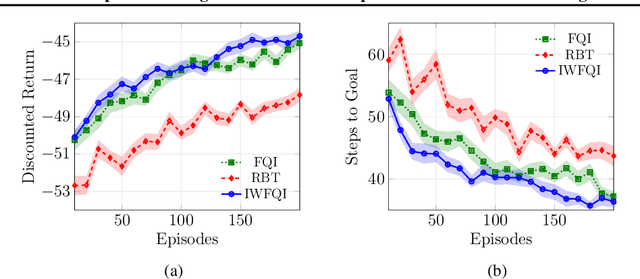
We consider the transfer of experience samples (i.e., tuples < s, a, s', r >) in reinforcement learning (RL), collected from a set of source tasks to improve the learning process in a given target task. Most of the related approaches focus on selecting the most relevant source samples for solving the target task, but then all the transferred samples are used without considering anymore the discrepancies between the task models. In this paper, we propose a model-based technique that automatically estimates the relevance (importance weight) of each source sample for solving the target task. In the proposed approach, all the samples are transferred and used by a batch RL algorithm to solve the target task, but their contribution to the learning process is proportional to their importance weight. By extending the results for importance weighting provided in supervised learning literature, we develop a finite-sample analysis of the proposed batch RL algorithm. Furthermore, we empirically compare the proposed algorithm to state-of-the-art approaches, showing that it achieves better learning performance and is very robust to negative transfer, even when some source tasks are significantly different from the target task.

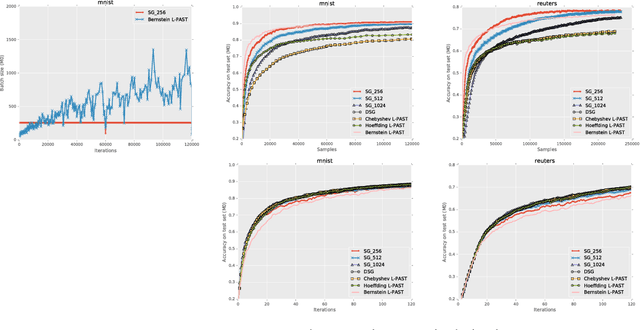
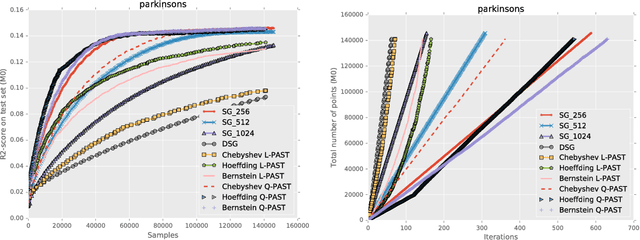
Cost-Sensitive Approach to Batch Size Adaptation for Gradient Descent

In this paper, we propose a novel approach to automatically determine the batch size in stochastic gradient descent methods. The choice of the batch size induces a trade-off between the accuracy of the gradient estimate and the cost in terms of samples of each update. We propose to determine the batch size by optimizing the ratio between a lower bound to a linear or quadratic Taylor approximation of the expected improvement and the number of samples used to estimate the gradient. The performance of the proposed approach is empirically compared with related methods on popular classification tasks. The work was presented at the NIPS workshop on Optimizing the Optimizers. Barcelona, Spain, 2016.

Multi-objective Reinforcement Learning with Continuous Pareto Frontier Approximation Supplementary Material

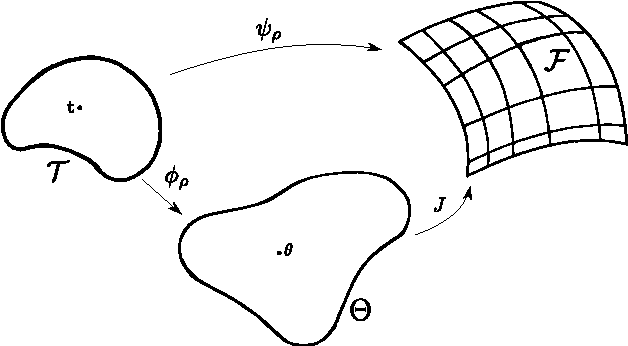
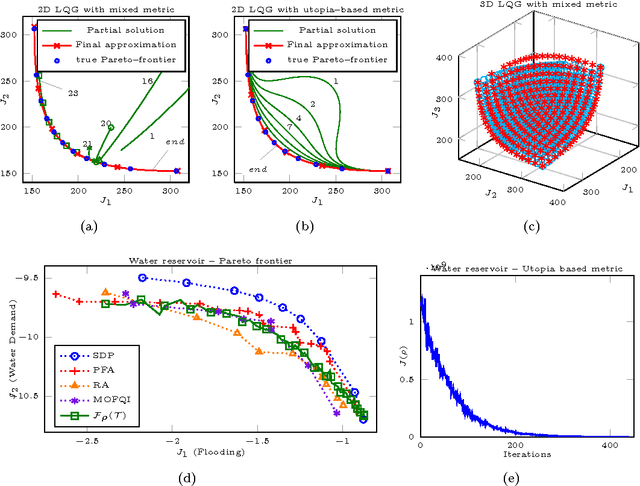
This document contains supplementary material for the paper "Multi-objective Reinforcement Learning with Continuous Pareto Frontier Approximation", published at the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI-15). The paper is about learning a continuous approximation of the Pareto frontier in Multi-Objective Markov Decision Problems (MOMDPs). We propose a policy-based approach that exploits gradient information to generate solutions close to the Pareto ones. Differently from previous policy-gradient multi-objective algorithms, where n optimization routines are use to have n solutions, our approach performs a single gradient-ascent run that at each step generates an improved continuous approximation of the Pareto frontier. The idea is to exploit a gradient-based approach to optimize the parameters of a function that defines a manifold in the policy parameter space so that the corresponding image in the objective space gets as close as possible to the Pareto frontier. Besides deriving how to compute and estimate such gradient, we will also discuss the non-trivial issue of defining a metric to assess the quality of the candidate Pareto frontiers. Finally, the properties of the proposed approach are empirically evaluated on two interesting MOMDPs.