An Approach to Model Interest for Planetary Rover through Dezert-Smarandache Theory

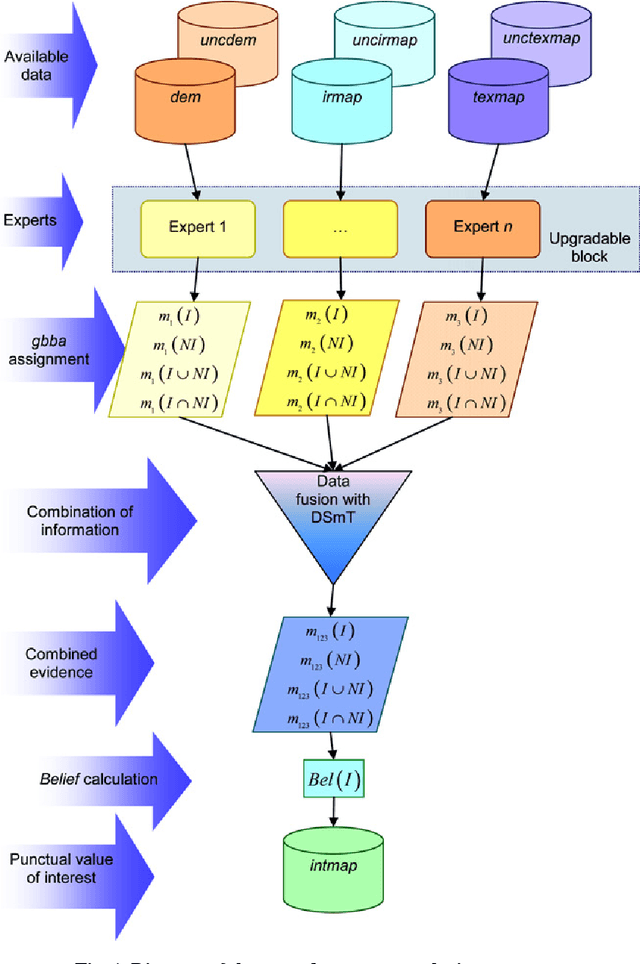
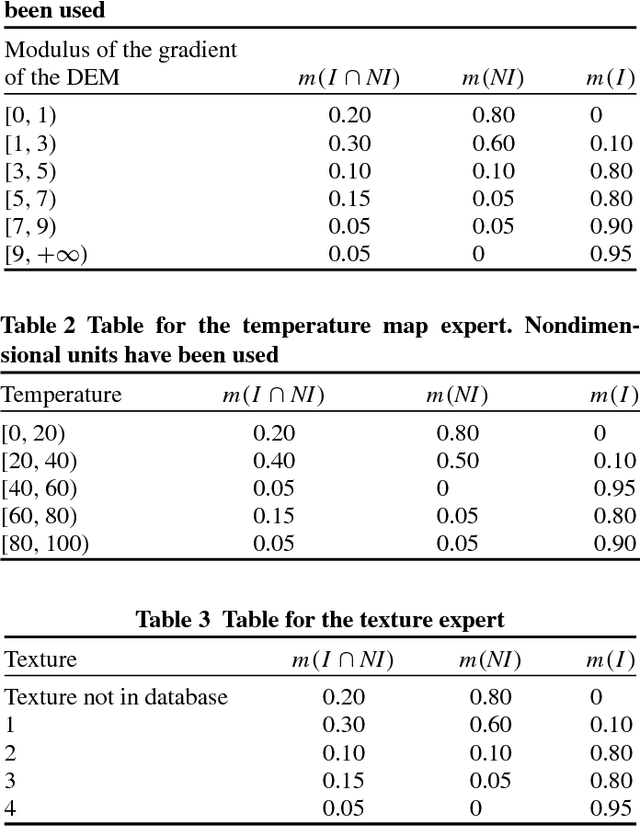
In this paper, we propose an approach for assigning an interest level to the goals of a planetary rover. Assigning an interest level to goals, allows the rover autonomously to transform and reallocate the goals. The interest level is defined by data-fusing payload and navigation information. The fusion yields an "interest map", that quantifies the level of interest of each area around the rover. In this way the planner can choose the most interesting scientific objectives to be analyzed, with limited human intervention, and reallocates its goals autonomously. The Dezert-Smarandache Theory of Plausible and Paradoxical Reasoning was used for information fusion: this theory allows dealing with vague and conflicting data. In particular, it allows us directly to model the behavior of the scientists that have to evaluate the relevance of a particular set of goals. The paper shows an application of the proposed approach to the generation of a reliable interest map.

MGA trajectory planning with an ACO-inspired algorithm

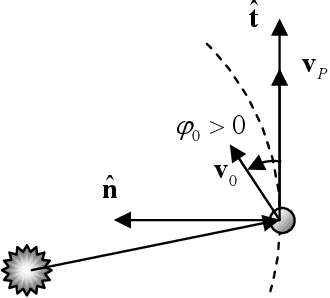
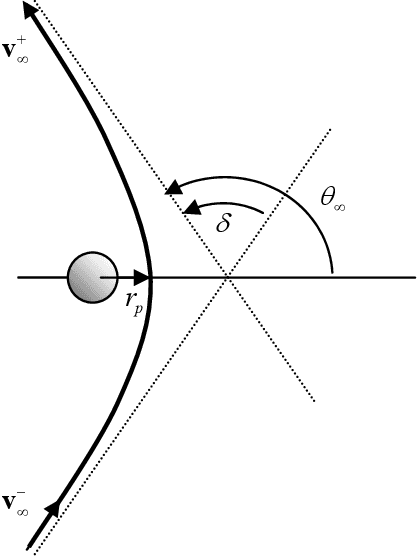
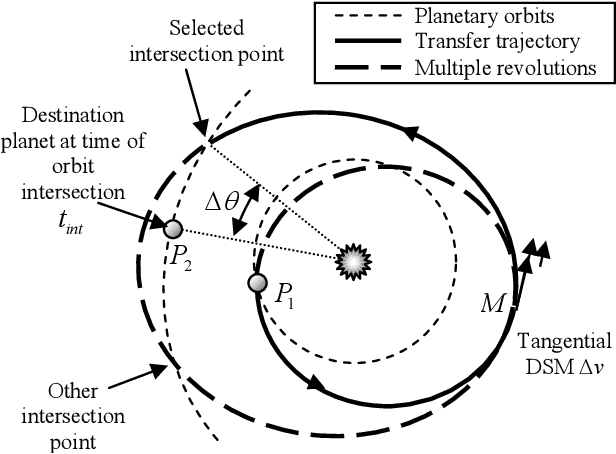
Given a set of celestial bodies, the problem of finding an optimal sequence of swing-bys, deep space manoeuvres (DSM) and transfer arcs connecting the elements of the set is combinatorial in nature. The number of possible paths grows exponentially with the number of celestial bodies. Therefore, the design of an optimal multiple gravity assist (MGA) trajectory is a NP-hard mixed combinatorial-continuous problem. Its automated solution would greatly improve the design of future space missions, allowing the assessment of a large number of alternative mission options in a short time. This work proposes to formulate the complete automated design of a multiple gravity assist trajectory as an autonomous planning and scheduling problem. The resulting scheduled plan will provide the optimal planetary sequence and a good estimation of the set of associated optimal trajectories. The trajectory model consists of a sequence of celestial bodies connected by twodimensional transfer arcs containing one DSM. For each transfer arc, the position of the planet and the spacecraft, at the time of arrival, are matched by varying the pericentre of the preceding swing-by, or the magnitude of the launch excess velocity, for the first arc. For each departure date, this model generates a full tree of possible transfers from the departure to the destination planet. Each leaf of the tree represents a planetary encounter and a possible way to reach that planet. An algorithm inspired by Ant Colony Optimization (ACO) is devised to explore the space of possible plans. The ants explore the tree from departure to destination adding one node at the time: every time an ant is at a node, a probability function is used to select a feasible direction. This approach to automatic trajectory planning is applied to the design of optimal transfers to Saturn and among the Galilean moons of Jupiter.