Solving hybrid machine learning tasks by traversing weight space geodesics

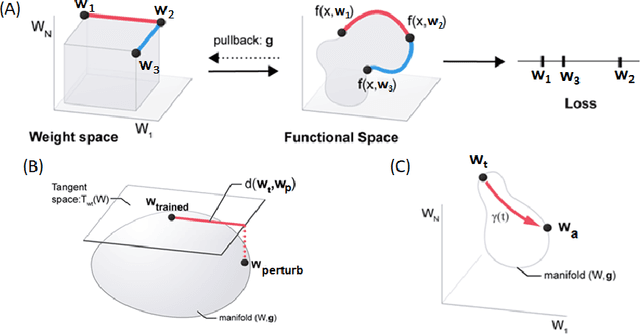
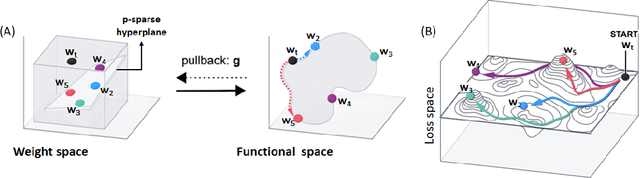
Machine learning problems have an intrinsic geometric structure as central objects including a neural network's weight space and the loss function associated with a particular task can be viewed as encoding the intrinsic geometry of a given machine learning problem. Therefore, geometric concepts can be applied to analyze and understand theoretical properties of machine learning strategies as well as to develop new algorithms. In this paper, we address three seemingly unrelated open questions in machine learning by viewing them through a unified framework grounded in differential geometry. Specifically, we view the weight space of a neural network as a manifold endowed with a Riemannian metric that encodes performance on specific tasks. By defining a metric, we can construct geodesic, minimum length, paths in weight space that represent sets of networks of equivalent or near equivalent functional performance on a specific task. We, then, traverse geodesic paths while identifying networks that satisfy a second objective. Inspired by the geometric insight, we apply our geodesic framework to 3 major applications: (i) Network sparsification (ii) Mitigating catastrophic forgetting by constructing networks with high performance on a series of objectives and (iii) Finding high-accuracy paths connecting distinct local optima of deep networks in the non-convex loss landscape. Our results are obtained on a wide range of network architectures (MLP, VGG11/16) trained on MNIST, CIFAR-10/100. Broadly, we introduce a geometric framework that unifies a range of machine learning objectives and that can be applied to multiple classes of neural network architectures.

Reinforcement Learning reveals fundamental limits on the mixing of active particles

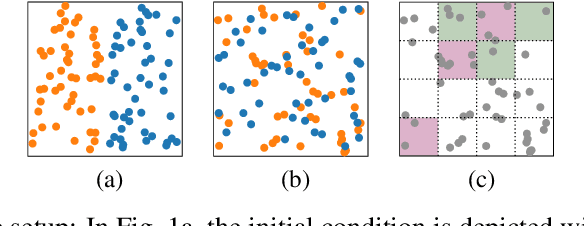
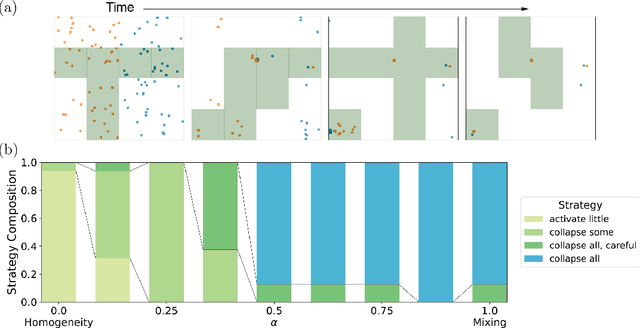
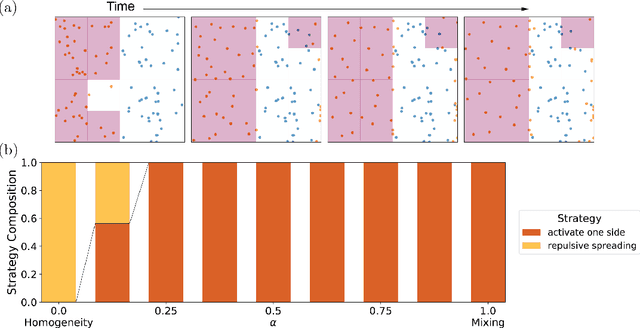
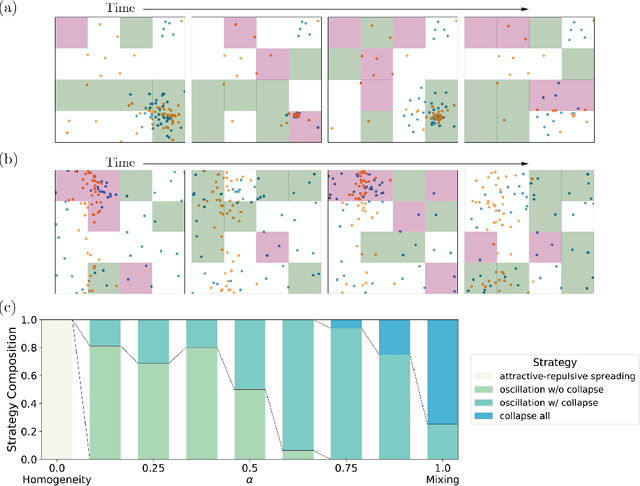
The control of far-from-equilibrium physical systems, including active materials, has emerged as an important area for the application of reinforcement learning (RL) strategies to derive control policies for physical systems. In active materials, non-linear dynamics and long-range interactions between particles prohibit closed-form descriptions of the system's dynamics and prevent explicit solutions to optimal control problems. Due to fundamental challenges in solving for explicit control strategies, RL has emerged as an approach to derive control strategies for far-from-equilibrium active matter systems. However, an important open question is how the mathematical structure and the physical properties of the active matter systems determine the tractability of RL for learning control policies. In this work, we show that RL can only find good strategies to the canonical active matter task of mixing for systems that combine attractive and repulsive particle interactions. Using mathematical results from dynamical systems theory, we relate the availability of both interaction types with the existence of hyperbolic dynamics and the ability of RL to find homogeneous mixing strategies. In particular, we show that for drag-dominated translational-invariant particle systems, hyperbolic dynamics and, therefore, mixing requires combining attractive and repulsive interactions. Broadly, our work demonstrates how fundamental physical and mathematical properties of dynamical systems can enable or constrain reinforcement learning-based control.

Sparsifying networks by traversing Geodesics

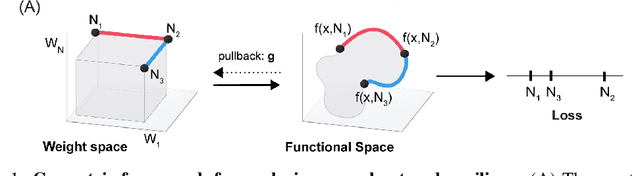
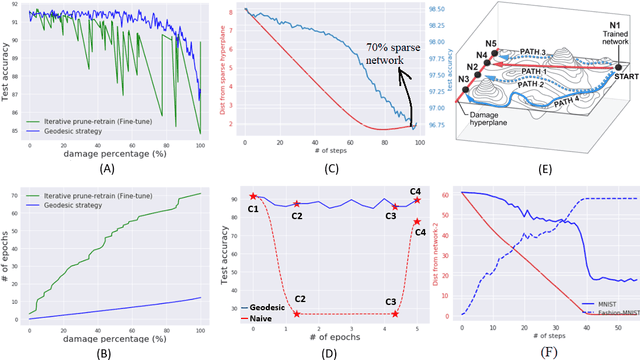
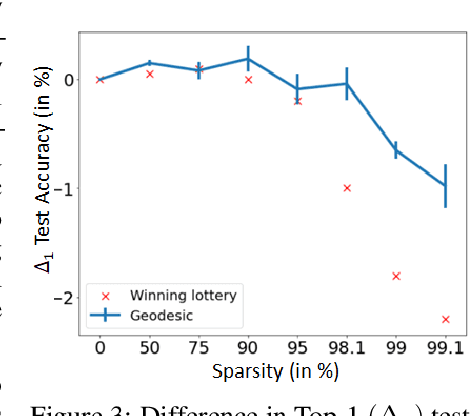
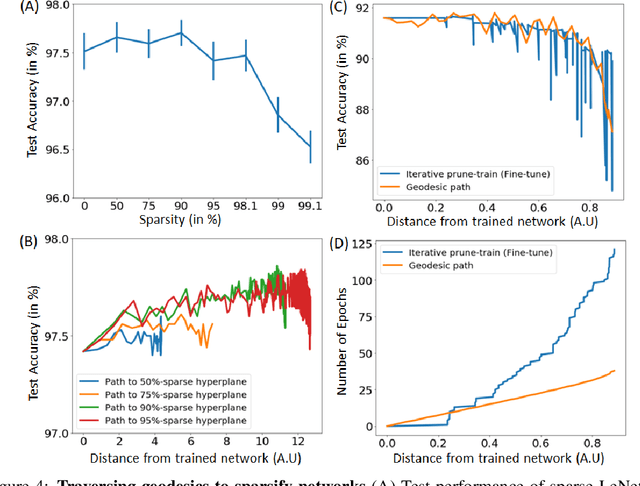
The geometry of weight spaces and functional manifolds of neural networks play an important role towards 'understanding' the intricacies of ML. In this paper, we attempt to solve certain open questions in ML, by viewing them through the lens of geometry, ultimately relating it to the discovery of points or paths of equivalent function in these spaces. We propose a mathematical framework to evaluate geodesics in the functional space, to find high-performance paths from a dense network to its sparser counterpart. Our results are obtained on VGG-11 trained on CIFAR-10 and MLP's trained on MNIST. Broadly, we demonstrate that the framework is general, and can be applied to a wide variety of problems, ranging from sparsification to alleviating catastrophic forgetting.

Self-organization of multi-layer spiking neural networks

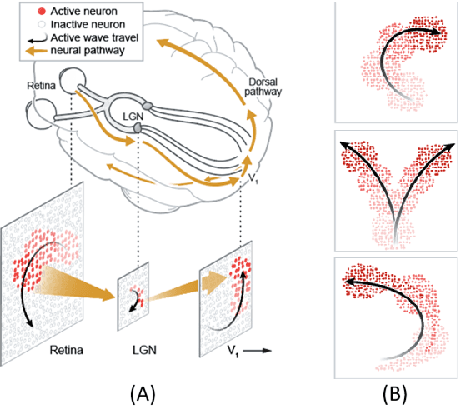
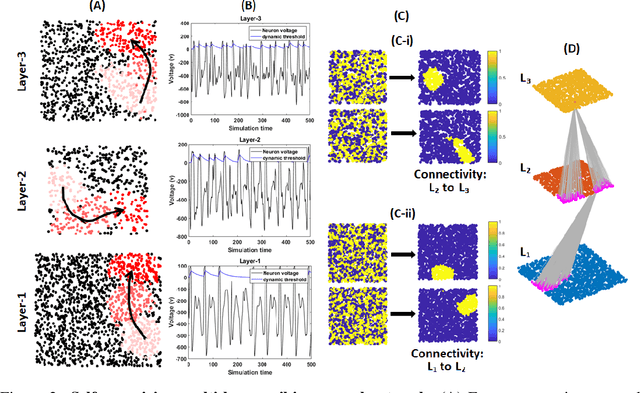
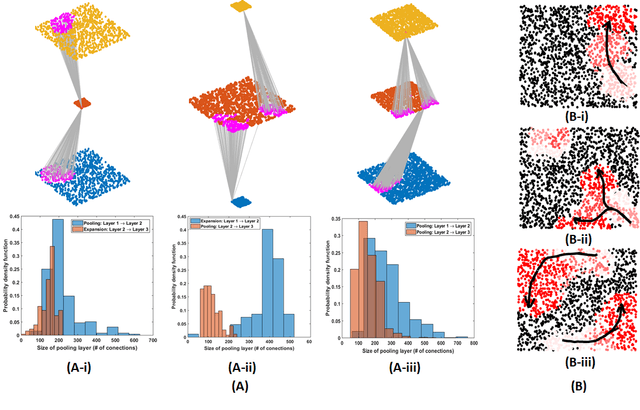
Living neural networks in our brains autonomously self-organize into large, complex architectures during early development to result in an organized and functional organic computational device. A key mechanism that enables the formation of complex architecture in the developing brain is the emergence of traveling spatio-temporal waves of neuronal activity across the growing brain. Inspired by this strategy, we attempt to efficiently self-organize large neural networks with an arbitrary number of layers into a wide variety of architectures. To achieve this, we propose a modular tool-kit in the form of a dynamical system that can be seamlessly stacked to assemble multi-layer neural networks. The dynamical system encapsulates the dynamics of spiking units, their inter/intra layer interactions as well as the plasticity rules that control the flow of information between layers. The key features of our tool-kit are (1) autonomous spatio-temporal waves across multiple layers triggered by activity in the preceding layer and (2) Spike-timing dependent plasticity (STDP) learning rules that update the inter-layer connectivity based on wave activity in the connecting layers. Our framework leads to the self-organization of a wide variety of architectures, ranging from multi-layer perceptrons to autoencoders. We also demonstrate that emergent waves can self-organize spiking network architecture to perform unsupervised learning, and networks can be coupled with a linear classifier to perform classification on classic image datasets like MNIST. Broadly, our work shows that a dynamical systems framework for learning can be used to self-organize large computational devices.

Geometric algorithms for predicting resilience and recovering damage in neural networks

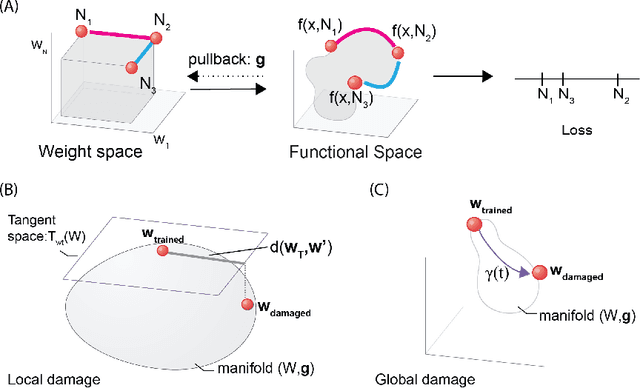
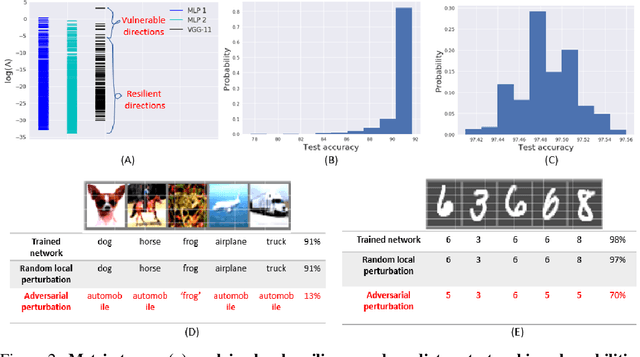
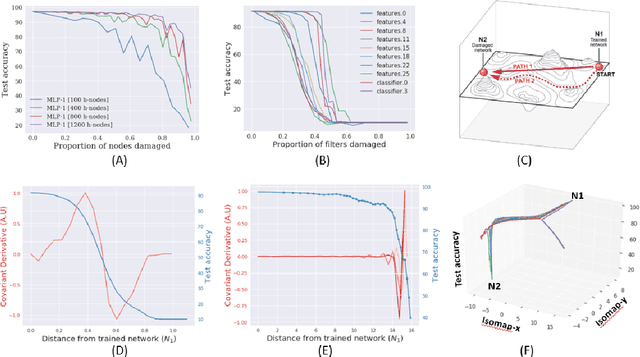
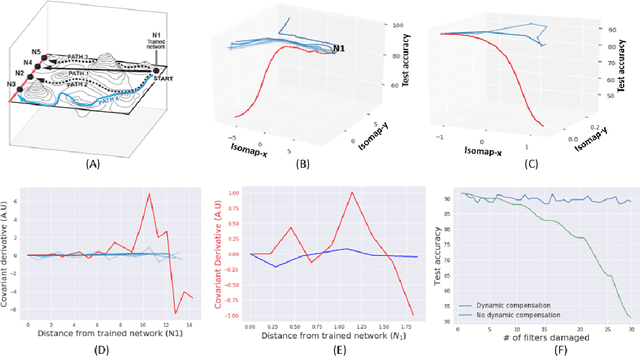
Biological neural networks have evolved to maintain performance despite significant circuit damage. To survive damage, biological network architectures have both intrinsic resilience to component loss and also activate recovery programs that adjust network weights through plasticity to stabilize performance. Despite the importance of resilience in technology applications, the resilience of artificial neural networks is poorly understood, and autonomous recovery algorithms have yet to be developed. In this paper, we establish a mathematical framework to analyze the resilience of artificial neural networks through the lens of differential geometry. Our geometric language provides natural algorithms that identify local vulnerabilities in trained networks as well as recovery algorithms that dynamically adjust networks to compensate for damage. We reveal striking vulnerabilities in commonly used image analysis networks, like MLP's and CNN's trained on MNIST and CIFAR10 respectively. We also uncover high-performance recovery paths that enable the same networks to dynamically re-adjust their parameters to compensate for damage. Broadly, our work provides procedures that endow artificial systems with resilience and rapid-recovery routines to enhance their integration with IoT devices as well as enable their deployment for critical applications.

Neural networks grown and self-organized by noise

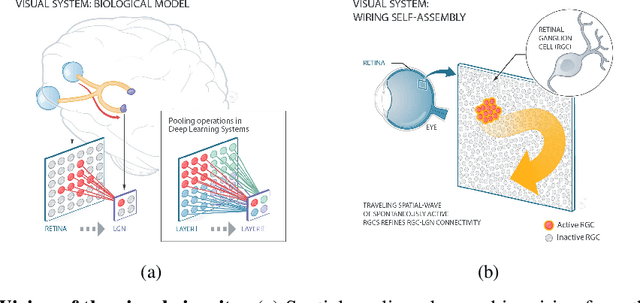
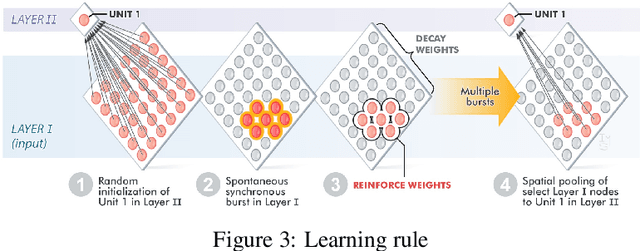
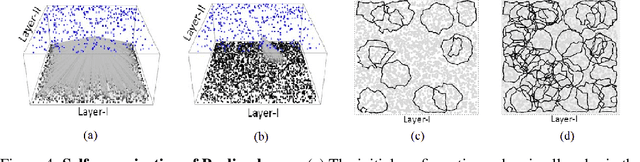
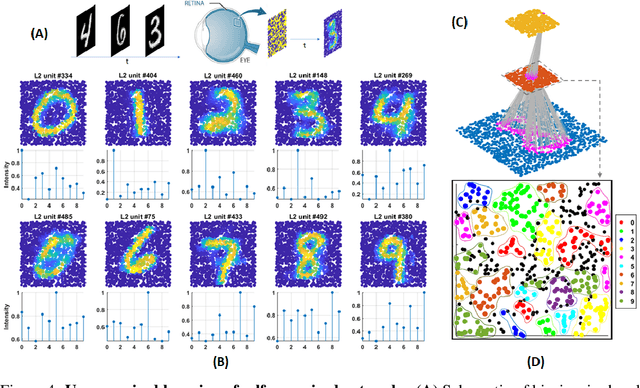
Living neural networks emerge through a process of growth and self-organization that begins with a single cell and results in a brain, an organized and functional computational device. Artificial neural networks, however, rely on human-designed, hand-programmed architectures for their remarkable performance. Can we develop artificial computational devices that can grow and self-organize without human intervention? In this paper, we propose a biologically inspired developmental algorithm that can 'grow' a functional, layered neural network from a single initial cell. The algorithm organizes inter-layer connections to construct a convolutional pooling layer, a key constituent of convolutional neural networks (CNN's). Our approach is inspired by the mechanisms employed by the early visual system to wire the retina to the lateral geniculate nucleus (LGN), days before animals open their eyes. The key ingredients for robust self-organization are an emergent spontaneous spatiotemporal activity wave in the first layer and a local learning rule in the second layer that 'learns' the underlying activity pattern in the first layer. The algorithm is adaptable to a wide-range of input-layer geometries, robust to malfunctioning units in the first layer, and so can be used to successfully grow and self-organize pooling architectures of different pool-sizes and shapes. The algorithm provides a primitive procedure for constructing layered neural networks through growth and self-organization. Broadly, our work shows that biologically inspired developmental algorithms can be applied to autonomously grow functional 'brains' in-silico.

Active Learning of Spin Network Models

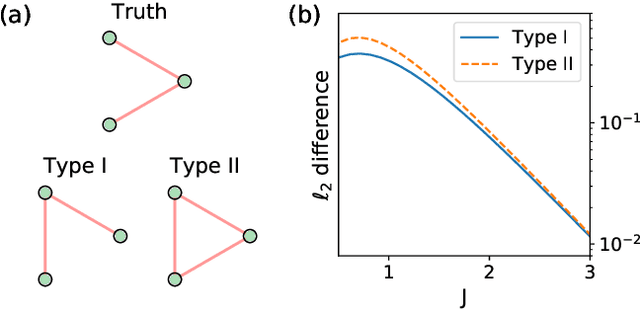
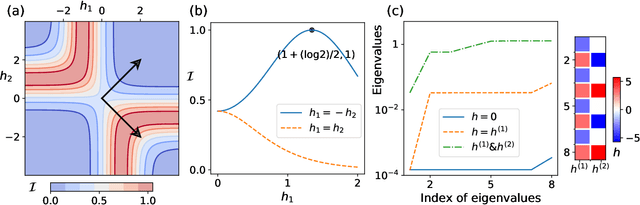
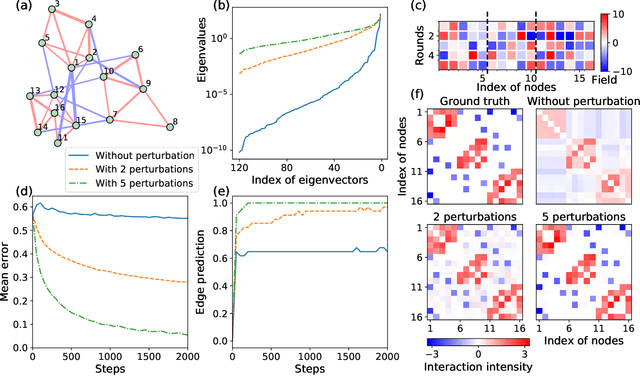
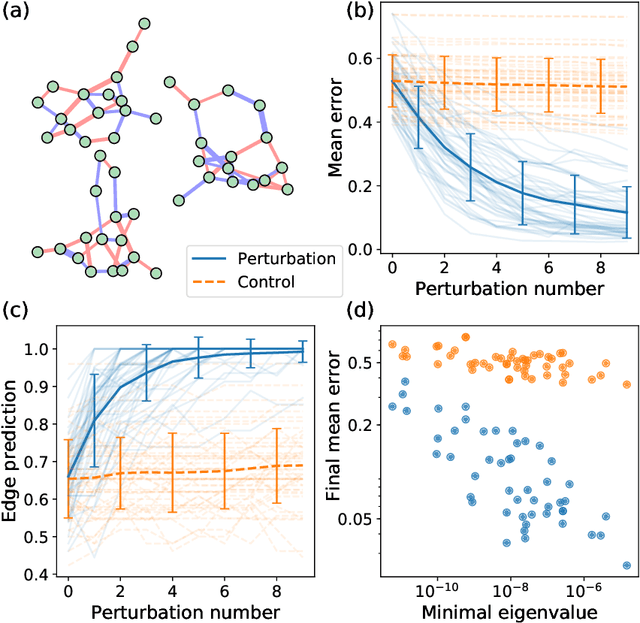
Complex networks can be modeled as a probabilistic graphical model, where the interactions between binary variables, "spins", on nodes are described by a coupling matrix that is inferred from observations. The inverse statistical problem of finding direct interactions is difficult, especially for large systems, because of the exponential growth in the possible number of states and the possible number of networks. In the context of the experimental sciences, well-controlled perturbations can be applied to a system, shedding light on the internal structure of the network. Therefore, we propose a method to improve the accuracy and efficiency of inference by iteratively applying perturbations to a network that are advantageous under a Bayesian framework. The spectrum of the empirical Fisher information can be used as a measure for the difficulty of the inference during the training process. We significantly improve the accuracy and efficiency of inference in medium-sized networks based on this strategy with a reasonable number of experimental queries. Our method could be powerful in the analysis of complex networks as well as in the rational design of experiments.