Oh SnapMMD! Forecasting Stochastic Dynamics Beyond the Schrödinger Bridge's End

Scientists often want to make predictions beyond the observed time horizon of "snapshot" data following latent stochastic dynamics. For example, in time course single-cell mRNA profiling, scientists have access to cellular transcriptional state measurements (snapshots) from different biological replicates at different time points, but they cannot access the trajectory of any one cell because measurement destroys the cell. Researchers want to forecast (e.g.) differentiation outcomes from early state measurements of stem cells. Recent Schr\"odinger-bridge (SB) methods are natural for interpolating between snapshots. But past SB papers have not addressed forecasting -- likely since existing methods either (1) reduce to following pre-set reference dynamics (chosen before seeing data) or (2) require the user to choose a fixed, state-independent volatility since they minimize a Kullback-Leibler divergence. Either case can lead to poor forecasting quality. In the present work, we propose a new framework, SnapMMD, that learns dynamics by directly fitting the joint distribution of both state measurements and observation time with a maximum mean discrepancy (MMD) loss. Unlike past work, our method allows us to infer unknown and state-dependent volatilities from the observed data. We show in a variety of real and synthetic experiments that our method delivers accurate forecasts. Moreover, our approach allows us to learn in the presence of incomplete state measurements and yields an $R^2$-style statistic that diagnoses fit. We also find that our method's performance at interpolation (and general velocity-field reconstruction) is at least as good as (and often better than) state-of-the-art in almost all of our experiments.

Boosting Statistic Learning with Synthetic Data from Pretrained Large Models

The rapid advancement of generative models, such as Stable Diffusion, raises a key question: how can synthetic data from these models enhance predictive modeling? While they can generate vast amounts of datasets, only a subset meaningfully improves performance. We propose a novel end-to-end framework that generates and systematically filters synthetic data through domain-specific statistical methods, selectively integrating high-quality samples for effective augmentation. Our experiments demonstrate consistent improvements in predictive performance across various settings, highlighting the potential of our framework while underscoring the inherent limitations of generative models for data augmentation. Despite the ability to produce large volumes of synthetic data, the proportion that effectively improves model performance is limited.

Active Learning of Spin Network Models

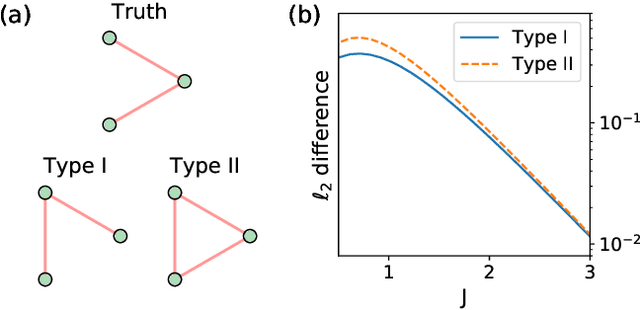
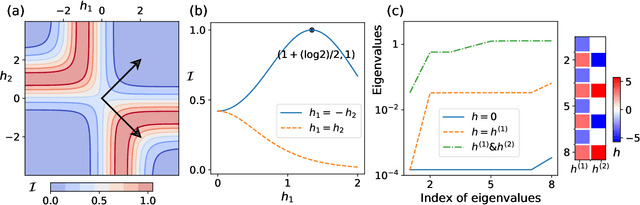
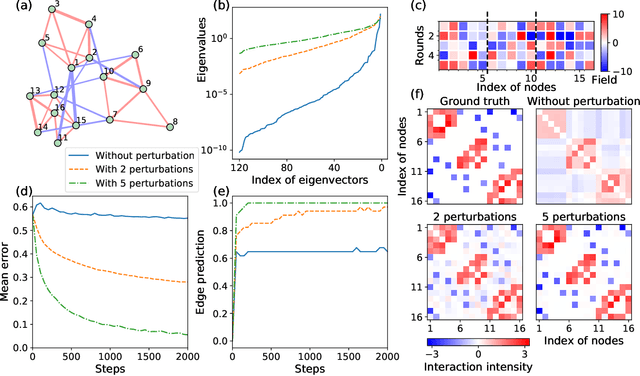
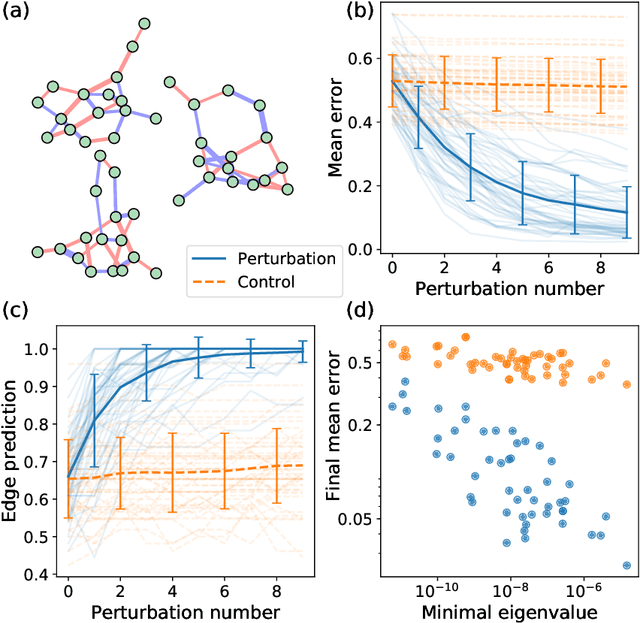
Complex networks can be modeled as a probabilistic graphical model, where the interactions between binary variables, "spins", on nodes are described by a coupling matrix that is inferred from observations. The inverse statistical problem of finding direct interactions is difficult, especially for large systems, because of the exponential growth in the possible number of states and the possible number of networks. In the context of the experimental sciences, well-controlled perturbations can be applied to a system, shedding light on the internal structure of the network. Therefore, we propose a method to improve the accuracy and efficiency of inference by iteratively applying perturbations to a network that are advantageous under a Bayesian framework. The spectrum of the empirical Fisher information can be used as a measure for the difficulty of the inference during the training process. We significantly improve the accuracy and efficiency of inference in medium-sized networks based on this strategy with a reasonable number of experimental queries. Our method could be powerful in the analysis of complex networks as well as in the rational design of experiments.