Efficient Collision-Avoidance Constraints for Ellipsoidal Obstacles in Optimal Control: Application to Path-Following MPC and UAVs

This article proposes a modular optimal control framework for local three-dimensional ellipsoidal obstacle avoidance, exemplarily applied to model predictive path-following control. Static as well as moving obstacles are considered. Central to the approach is a computationally efficient and continuously differentiable condition for detecting collisions with ellipsoidal obstacles. A novel two-stage optimization approach mitigates numerical issues arising from the structure of the resulting optimal control problem. The effectiveness of the approach is demonstrated through simulations and real-world experiments with the Crazyflie quadrotor. This represents the first hardware demonstration of an MPC controller of this kind for UAVs in a three-dimensional task.

Efficient Avoidance of Ellipsoidal Obstacles with Model Predictive Control for Mobile Robots and Vehicles

In real-world applications of mobile robots, collision avoidance is of critical importance. Typically, global motion planning in constrained environments is addressed through high-level control schemes. However, additionally integrating local collision avoidance into robot motion control offers significant advantages. For instance, it reduces the reliance on heuristics and conservatism that can arise from a two-stage approach separating local collision avoidance and control. Moreover, using model predictive control (MPC), a robot's full potential can be harnessed by considering jointly local collision avoidance, the robot's dynamics, and actuation constraints. In this context, the present paper focuses on obstacle avoidance for wheeled mobile robots, where both the robot's and obstacles' occupied volumes are modeled as ellipsoids. To this end, a computationally efficient overlap test, that works for arbitrary ellipsoids, is conducted and novelly integrated into the MPC framework. We propose a particularly efficient implementation tailored to robots moving in the plane. The functionality of the proposed obstacle-avoiding MPC is demonstrated for two exemplary types of kinematics by means of simulations. A hardware experiment using a real-world wheeled mobile robot shows transferability to reality and real-time applicability. The general computational approach to ellipsoidal obstacle avoidance can also be applied to other robotic systems and vehicles as well as three-dimensional scenarios.

Robust Model Predictive Longitudinal Position Tracking Control for an Autonomous Vehicle Based on Multiple Models

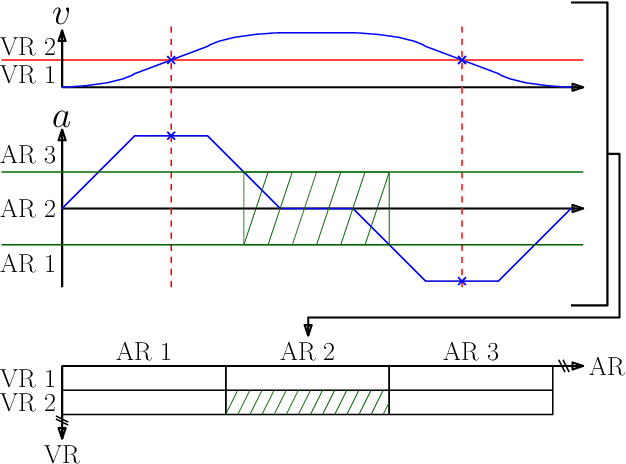
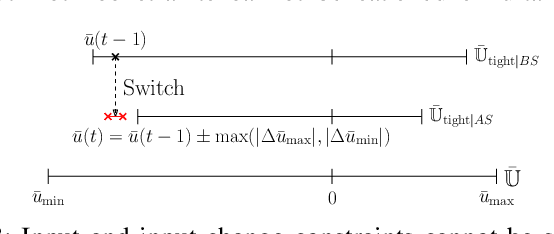
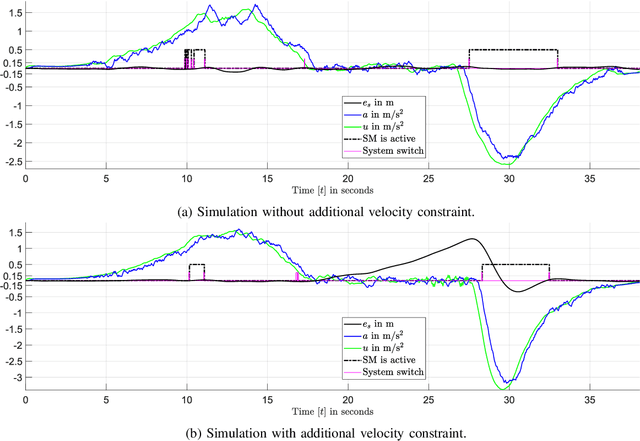
The aim of this work is to control the longitudinal position of an autonomous vehicle with an internal combustion engine. The powertrain has an inherent dead-time characteristic and constraints on physical states apply since the vehicle is neither able to accelerate arbitrarily strong, nor to drive arbitrarily fast. A model predictive controller (MPC) is able to cope with both of the aforementioned system properties. MPC heavily relies on a model and therefore a strategy on how to obtain multiple linear state space prediction models of the nonlinear system via input/output data system identification from acceleration data is given. The models are identified in different regions of the vehicle dynamics in order to obtain more accurate predictions. The still remaining plant-model mismatch can be expressed as an additive disturbance which can be handled through robust control theory. Therefore modifications to the models for applying robust MPC tracking control theory are described. Then a controller which guarantees robust constraint satisfaction and recursive feasibility is designed. As a next step, modifications to apply the controller on multiple models are discussed. In this context, a model switching strategy is provided and theoretical and computational limitations are pointed out. Lastly, simulation results are presented and discussed, including computational load when switching between systems.