Collapsing Taylor Mode Automatic Differentiation

Computing partial differential equation (PDE) operators via nested backpropagation is expensive, yet popular, and severely restricts their utility for scientific machine learning. Recent advances, like the forward Laplacian and randomizing Taylor mode automatic differentiation (AD), propose forward schemes to address this. We introduce an optimization technique for Taylor mode that 'collapses' derivatives by rewriting the computational graph, and demonstrate how to apply it to general linear PDE operators, and randomized Taylor mode. The modifications simply require propagating a sum up the computational graph, which could -- or should -- be done by a machine learning compiler, without exposing complexity to users. We implement our collapsing procedure and evaluate it on popular PDE operators, confirming it accelerates Taylor mode and outperforms nested backpropagation.

Improving Energy Natural Gradient Descent through Woodbury, Momentum, and Randomization

Natural gradient methods significantly accelerate the training of Physics-Informed Neural Networks (PINNs), but are often prohibitively costly. We introduce a suite of techniques to improve the accuracy and efficiency of energy natural gradient descent (ENGD) for PINNs. First, we leverage the Woodbury formula to dramatically reduce the computational complexity of ENGD. Second, we adapt the Subsampled Projected-Increment Natural Gradient Descent algorithm from the variational Monte Carlo literature to accelerate the convergence. Third, we explore the use of randomized algorithms to further reduce the computational cost in the case of large batch sizes. We find that randomization accelerates progress in the early stages of training for low-dimensional problems, and we identify key barriers to attaining acceleration in other scenarios. Our numerical experiments demonstrate that our methods outperform previous approaches, achieving the same $L^2$ error as the original ENGD up to $75\times$ faster.

Dynamical Measure Transport and Neural PDE Solvers for Sampling

The task of sampling from a probability density can be approached as transporting a tractable density function to the target, known as dynamical measure transport. In this work, we tackle it through a principled unified framework using deterministic or stochastic evolutions described by partial differential equations (PDEs). This framework incorporates prior trajectory-based sampling methods, such as diffusion models or Schr\"odinger bridges, without relying on the concept of time-reversals. Moreover, it allows us to propose novel numerical methods for solving the transport task and thus sampling from complicated targets without the need for the normalization constant or data samples. We employ physics-informed neural networks (PINNs) to approximate the respective PDE solutions, implying both conceptional and computational advantages. In particular, PINNs allow for simulation- and discretization-free optimization and can be trained very efficiently, leading to significantly better mode coverage in the sampling task compared to alternative methods. Moreover, they can readily be fine-tuned with Gauss-Newton methods to achieve high accuracy in sampling.

Achieving High Accuracy with PINNs via Energy Natural Gradients

We propose energy natural gradient descent, a natural gradient method with respect to a Hessian-induced Riemannian metric as an optimization algorithm for physics-informed neural networks (PINNs) and the deep Ritz method. As a main motivation we show that the update direction in function space resulting from the energy natural gradient corresponds to the Newton direction modulo an orthogonal projection onto the model's tangent space. We demonstrate experimentally that energy natural gradient descent yields highly accurate solutions with errors several orders of magnitude smaller than what is obtained when training PINNs with standard optimizers like gradient descent or Adam, even when those are allowed significantly more computation time.

The Deep Ritz Method for Parametric $p$-Dirichlet Problems

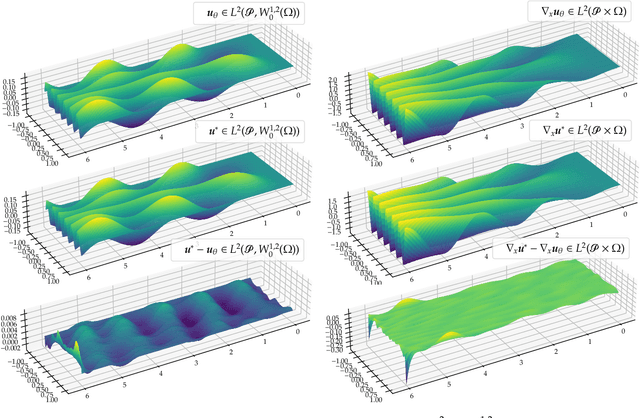
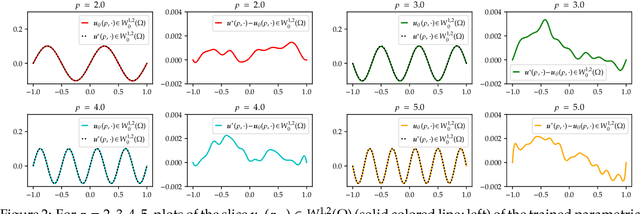
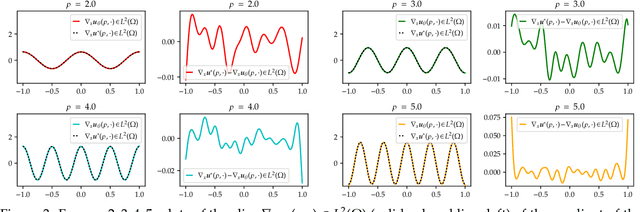
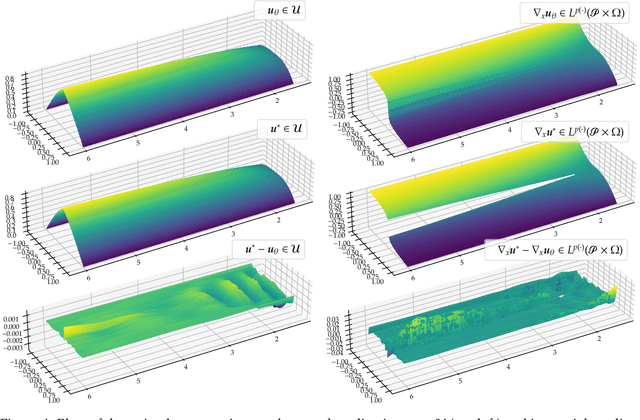
We establish error estimates for the approximation of parametric $p$-Dirichlet problems deploying the Deep Ritz Method. Parametric dependencies include, e.g., varying geometries and exponents $p\in (1,\infty)$. Combining the derived error estimates with quantitative approximation theorems yields error decay rates and establishes that the Deep Ritz Method retains the favorable approximation capabilities of neural networks in the approximation of high dimensional functions which makes the method attractive for parametric problems. Finally, we present numerical examples to illustrate potential applications.

Error Estimates for the Variational Training of Neural Networks with Boundary Penalty

We establish estimates on the error made by the Ritz method for quadratic energies on the space $H^1(\Omega)$ in the approximation of the solution of variational problems with different boundary conditions. Special attention is paid to the case of Dirichlet boundary values which are treated with the boundary penalty method. We consider arbitrary and in general non linear classes $V\subseteq H^1(\Omega)$ of ansatz functions and estimate the error in dependence of the optimisation accuracy, the approximation capabilities of the ansatz class and - in the case of Dirichlet boundary values - the penalisation strength $\lambda$. For non-essential boundary conditions the error of the Ritz method decays with the same rate as the approximation rate of the ansatz classes. For the boundary penalty method we obtain that given an approximation rate of $r$ in $H^1(\Omega)$ and an approximation rate of $s$ in $L^2(\partial\Omega)$ of the ansatz classes, the optimal decay rate of the estimated error is $\min(s/2, r) \in [r/2, r]$ and achieved by choosing $\lambda_n\sim n^{s}$. We discuss how this rate can be improved, the relation to existing estimates for finite element functions as well as the implications for ansatz classes which are given through ReLU networks. Finally, we use the notion of $\Gamma$-convergence to show that the Ritz method converges for a wide class of energies including nonlinear stationary PDEs like the $p$-Laplace.

Deep Ritz revisited

Recently, progress has been made in the application of neural networks to the numerical analysis of partial differential equations (PDEs). In the latter the variational formulation of the Poisson problem is used in order to obtain an objective function - a regularised Dirichlet energy - that was used for the optimisation of some neural networks. In this notes we use the notion of $\Gamma$-convergence to show that ReLU networks of growing architecture that are trained with respect to suitably regularised Dirichlet energies converge to the true solution of the Poisson problem. We discuss how this approach generalises to arbitrary variational problems under certain universality assumptions of neural networks and see that this covers some nonlinear stationary PDEs like the $p$-Laplace.