Strong Asymptotic Assertions for Discrete MDL in Regression and Classification

We study the properties of the MDL (or maximum penalized complexity) estimator for Regression and Classification, where the underlying model class is countable. We show in particular a finite bound on the Hellinger losses under the only assumption that there is a "true" model contained in the class. This implies almost sure convergence of the predictive distribution to the true one at a fast rate. It corresponds to Solomonoff's central theorem of universal induction, however with a bound that is exponentially larger.

Master Algorithms for Active Experts Problems based on Increasing Loss Values

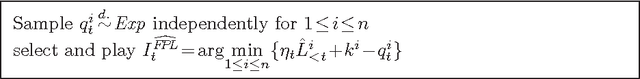
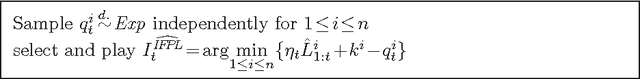
We specify an experts algorithm with the following characteristics: (a) it uses only feedback from the actions actually chosen (bandit setup), (b) it can be applied with countably infinite expert classes, and (c) it copes with losses that may grow in time appropriately slowly. We prove loss bounds against an adaptive adversary. From this, we obtain master algorithms for "active experts problems", which means that the master's actions may influence the behavior of the adversary. Our algorithm can significantly outperform standard experts algorithms on such problems. Finally, we combine it with a universal expert class. This results in a (computationally infeasible) universal master algorithm which performs - in a certain sense - almost as well as any computable strategy, for any online problem.

Fast Non-Parametric Bayesian Inference on Infinite Trees

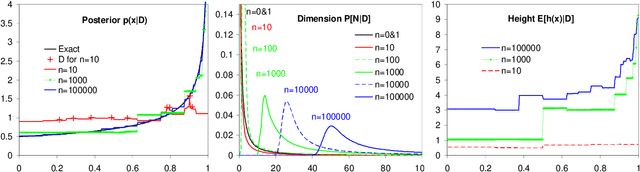
Given i.i.d. data from an unknown distribution, we consider the problem of predicting future items. An adaptive way to estimate the probability density is to recursively subdivide the domain to an appropriate data-dependent granularity. A Bayesian would assign a data-independent prior probability to "subdivide", which leads to a prior over infinite(ly many) trees. We derive an exact, fast, and simple inference algorithm for such a prior, for the data evidence, the predictive distribution, the effective model dimension, and other quantities.

Universal Sequential Decisions in Unknown Environments

We give a brief introduction to the AIXI model, which unifies and overcomes the limitations of sequential decision theory and universal Solomonoff induction. While the former theory is suited for active agents in known environments, the latter is suited for passive prediction of unknown environments.

Universal Convergence of Semimeasures on Individual Random Sequences

Solomonoff's central result on induction is that the posterior of a universal semimeasure M converges rapidly and with probability 1 to the true sequence generating posterior mu, if the latter is computable. Hence, M is eligible as a universal sequence predictor in case of unknown mu. Despite some nearby results and proofs in the literature, the stronger result of convergence for all (Martin-Loef) random sequences remained open. Such a convergence result would be particularly interesting and natural, since randomness can be defined in terms of M itself. We show that there are universal semimeasures M which do not converge for all random sequences, i.e. we give a partial negative answer to the open problem. We also provide a positive answer for some non-universal semimeasures. We define the incomputable measure D as a mixture over all computable measures and the enumerable semimeasure W as a mixture over all enumerable nearly-measures. We show that W converges to D and D to mu on all random sequences. The Hellinger distance measuring closeness of two distributions plays a central role.

On the Convergence Speed of MDL Predictions for Bernoulli Sequences

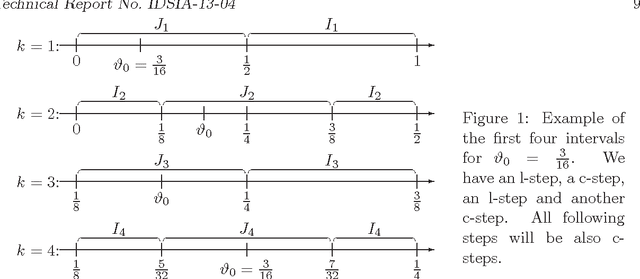
We consider the Minimum Description Length principle for online sequence prediction. If the underlying model class is discrete, then the total expected square loss is a particularly interesting performance measure: (a) this quantity is bounded, implying convergence with probability one, and (b) it additionally specifies a `rate of convergence'. Generally, for MDL only exponential loss bounds hold, as opposed to the linear bounds for a Bayes mixture. We show that this is even the case if the model class contains only Bernoulli distributions. We derive a new upper bound on the prediction error for countable Bernoulli classes. This implies a small bound (comparable to the one for Bayes mixtures) for certain important model classes. The results apply to many Machine Learning tasks including classification and hypothesis testing. We provide arguments that our theorems generalize to countable classes of i.i.d. models.

Prediction with Expert Advice by Following the Perturbed Leader for General Weights

When applying aggregating strategies to Prediction with Expert Advice, the learning rate must be adaptively tuned. The natural choice of sqrt(complexity/current loss) renders the analysis of Weighted Majority derivatives quite complicated. In particular, for arbitrary weights there have been no results proven so far. The analysis of the alternative "Follow the Perturbed Leader" (FPL) algorithm from Kalai (2003} (based on Hannan's algorithm) is easier. We derive loss bounds for adaptive learning rate and both finite expert classes with uniform weights and countable expert classes with arbitrary weights. For the former setup, our loss bounds match the best known results so far, while for the latter our results are (to our knowledge) new.

Convergence of Discrete MDL for Sequential Prediction

We study the properties of the Minimum Description Length principle for sequence prediction, considering a two-part MDL estimator which is chosen from a countable class of models. This applies in particular to the important case of universal sequence prediction, where the model class corresponds to all algorithms for some fixed universal Turing machine (this correspondence is by enumerable semimeasures, hence the resulting models are stochastic). We prove convergence theorems similar to Solomonoff's theorem of universal induction, which also holds for general Bayes mixtures. The bound characterizing the convergence speed for MDL predictions is exponentially larger as compared to Bayes mixtures. We observe that there are at least three different ways of using MDL for prediction. One of these has worse prediction properties, for which predictions only converge if the MDL estimator stabilizes. We establish sufficient conditions for this to occur. Finally, some immediate consequences for complexity relations and randomness criteria are proven.

Tournament versus Fitness Uniform Selection

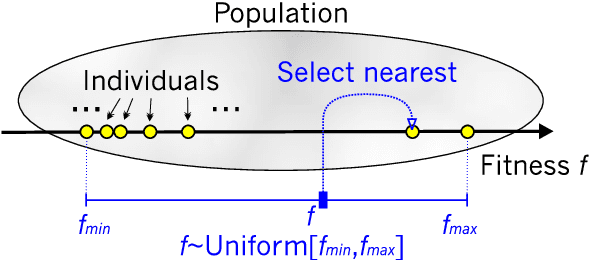
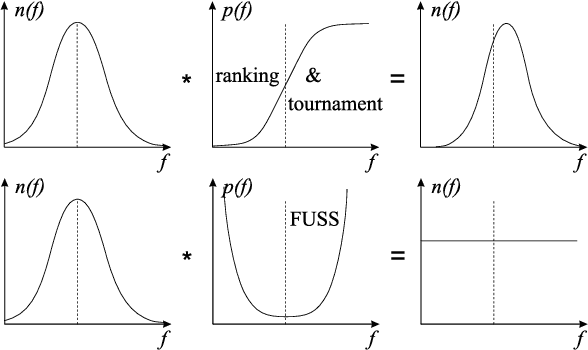
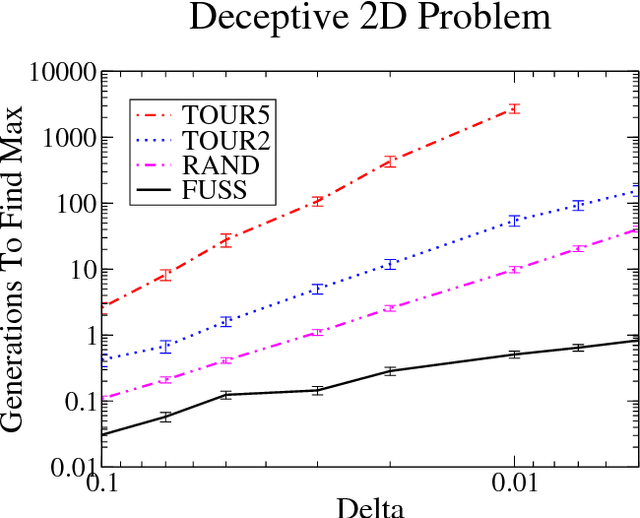
In evolutionary algorithms a critical parameter that must be tuned is that of selection pressure. If it is set too low then the rate of convergence towards the optimum is likely to be slow. Alternatively if the selection pressure is set too high the system is likely to become stuck in a local optimum due to a loss of diversity in the population. The recent Fitness Uniform Selection Scheme (FUSS) is a conceptually simple but somewhat radical approach to addressing this problem - rather than biasing the selection towards higher fitness, FUSS biases selection towards sparsely populated fitness levels. In this paper we compare the relative performance of FUSS with the well known tournament selection scheme on a range of problems.

Distribution of Mutual Information from Complete and Incomplete Data

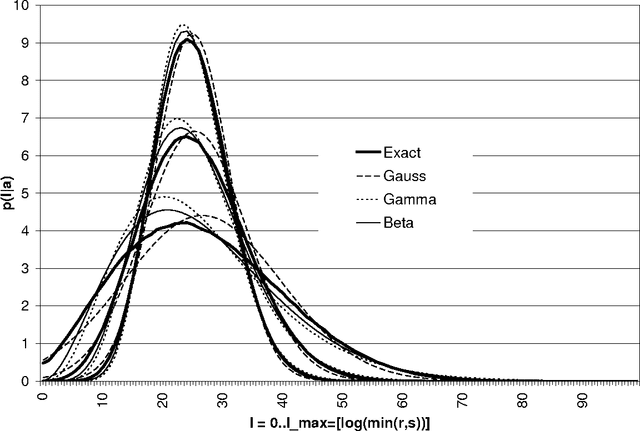
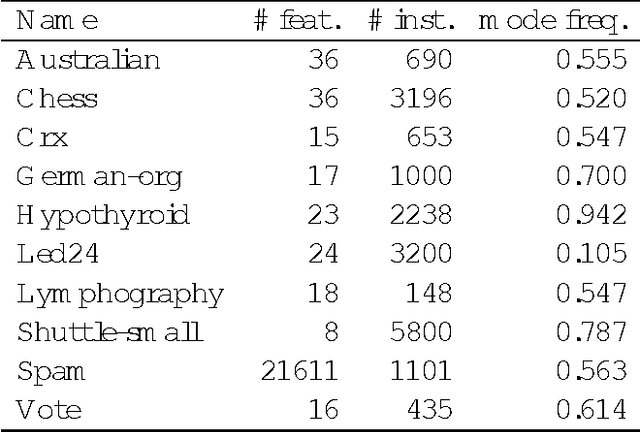
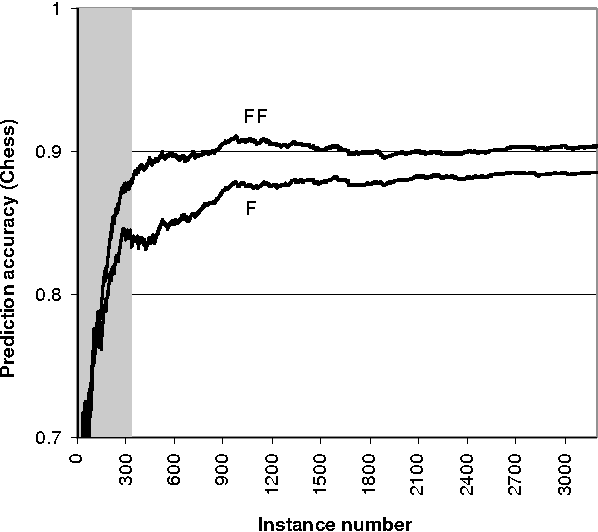
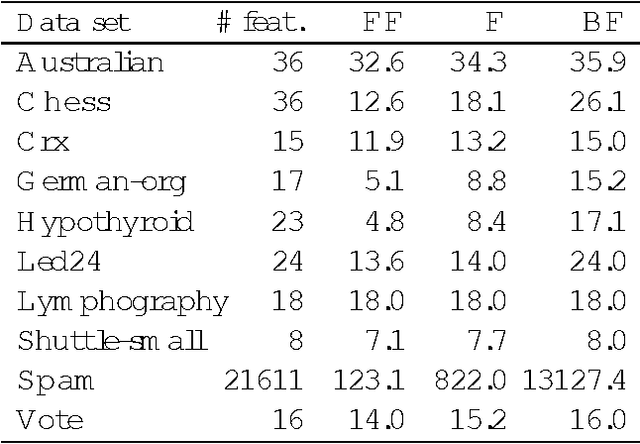
Mutual information is widely used, in a descriptive way, to measure the stochastic dependence of categorical random variables. In order to address questions such as the reliability of the descriptive value, one must consider sample-to-population inferential approaches. This paper deals with the posterior distribution of mutual information, as obtained in a Bayesian framework by a second-order Dirichlet prior distribution. The exact analytical expression for the mean, and analytical approximations for the variance, skewness and kurtosis are derived. These approximations have a guaranteed accuracy level of the order O(1/n^3), where n is the sample size. Leading order approximations for the mean and the variance are derived in the case of incomplete samples. The derived analytical expressions allow the distribution of mutual information to be approximated reliably and quickly. In fact, the derived expressions can be computed with the same order of complexity needed for descriptive mutual information. This makes the distribution of mutual information become a concrete alternative to descriptive mutual information in many applications which would benefit from moving to the inductive side. Some of these prospective applications are discussed, and one of them, namely feature selection, is shown to perform significantly better when inductive mutual information is used.