Learning to Compensate Photovoltaic Power Fluctuations from Images of the Sky by Imitating an Optimal Policy

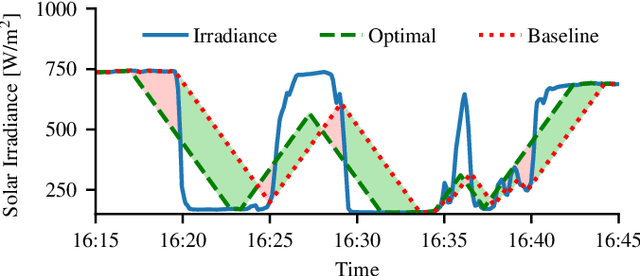
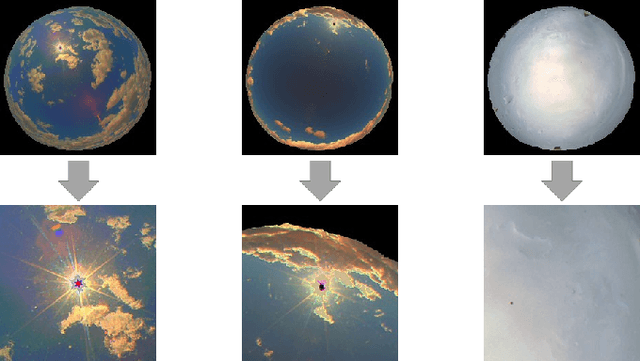
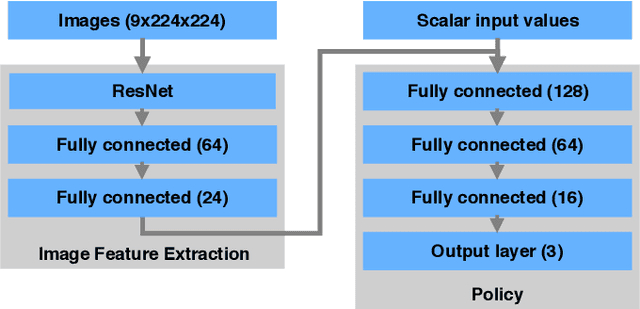
The energy output of photovoltaic (PV) power plants depends on the environment and thus fluctuates over time. As a result, PV power can cause instability in the power grid, in particular when increasingly used. Limiting the rate of change of the power output is a common way to mitigate these fluctuations, often with the help of large batteries. A reactive controller that uses these batteries to compensate ramps works in practice, but causes stress on the battery due to a high energy throughput. In this paper, we present a deep learning approach that uses images of the sky to compensate power fluctuations predictively and reduces battery stress. In particular, we show that the optimal control policy can be computed using information that is only available in hindsight. Based on this, we use imitation learning to train a neural network that approximates this hindsight-optimal policy, but uses only currently available sky images and sensor data. We evaluate our method on a large dataset of measurements and images from a real power plant and show that the trained policy reduces stress on the battery.

MDL Convergence Speed for Bernoulli Sequences

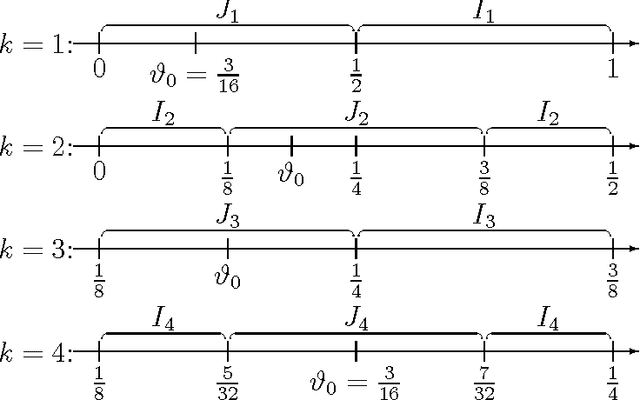
The Minimum Description Length principle for online sequence estimation/prediction in a proper learning setup is studied. If the underlying model class is discrete, then the total expected square loss is a particularly interesting performance measure: (a) this quantity is finitely bounded, implying convergence with probability one, and (b) it additionally specifies the convergence speed. For MDL, in general one can only have loss bounds which are finite but exponentially larger than those for Bayes mixtures. We show that this is even the case if the model class contains only Bernoulli distributions. We derive a new upper bound on the prediction error for countable Bernoulli classes. This implies a small bound (comparable to the one for Bayes mixtures) for certain important model classes. We discuss the application to Machine Learning tasks such as classification and hypothesis testing, and generalization to countable classes of i.i.d. models.

Universal Learning of Repeated Matrix Games

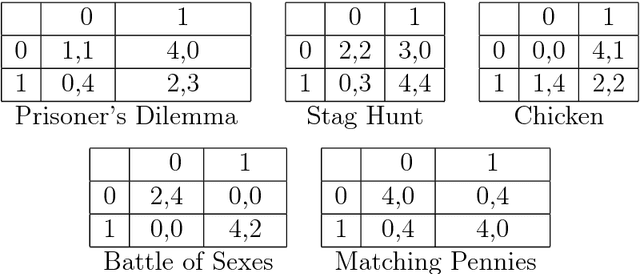
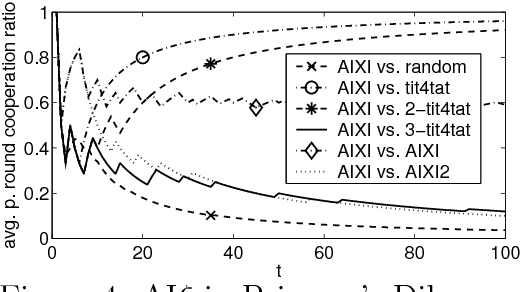
We study and compare the learning dynamics of two universal learning algorithms, one based on Bayesian learning and the other on prediction with expert advice. Both approaches have strong asymptotic performance guarantees. When confronted with the task of finding good long-term strategies in repeated 2x2 matrix games, they behave quite differently.

FPL Analysis for Adaptive Bandits

A main problem of "Follow the Perturbed Leader" strategies for online decision problems is that regret bounds are typically proven against oblivious adversary. In partial observation cases, it was not clear how to obtain performance guarantees against adaptive adversary, without worsening the bounds. We propose a conceptually simple argument to resolve this problem. Using this, a regret bound of O(t^(2/3)) for FPL in the adversarial multi-armed bandit problem is shown. This bound holds for the common FPL variant using only the observations from designated exploration rounds. Using all observations allows for the stronger bound of O(t^(1/2)), matching the best bound known so far (and essentially the known lower bound) for adversarial bandits. Surprisingly, this variant does not even need explicit exploration, it is self-stabilizing. However the sampling probabilities have to be either externally provided or approximated to sufficient accuracy, using O(t^2 log t) samples in each step.

Defensive Universal Learning with Experts

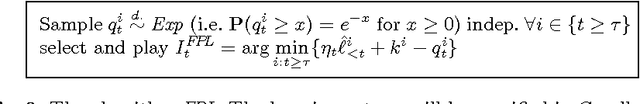
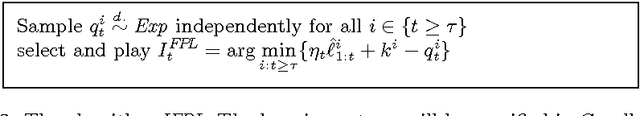
This paper shows how universal learning can be achieved with expert advice. To this aim, we specify an experts algorithm with the following characteristics: (a) it uses only feedback from the actions actually chosen (bandit setup), (b) it can be applied with countably infinite expert classes, and (c) it copes with losses that may grow in time appropriately slowly. We prove loss bounds against an adaptive adversary. From this, we obtain a master algorithm for "reactive" experts problems, which means that the master's actions may influence the behavior of the adversary. Our algorithm can significantly outperform standard experts algorithms on such problems. Finally, we combine it with a universal expert class. The resulting universal learner performs -- in a certain sense -- almost as well as any computable strategy, for any online decision problem. We also specify the (worst-case) convergence speed, which is very slow.

Asymptotics of Discrete MDL for Online Prediction

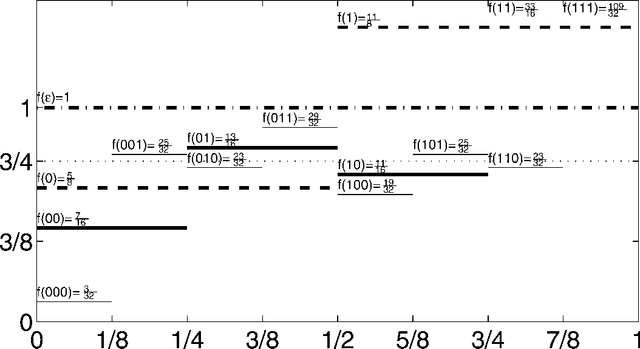
Minimum Description Length (MDL) is an important principle for induction and prediction, with strong relations to optimal Bayesian learning. This paper deals with learning non-i.i.d. processes by means of two-part MDL, where the underlying model class is countable. We consider the online learning framework, i.e. observations come in one by one, and the predictor is allowed to update his state of mind after each time step. We identify two ways of predicting by MDL for this setup, namely a static} and a dynamic one. (A third variant, hybrid MDL, will turn out inferior.) We will prove that under the only assumption that the data is generated by a distribution contained in the model class, the MDL predictions converge to the true values almost surely. This is accomplished by proving finite bounds on the quadratic, the Hellinger, and the Kullback-Leibler loss of the MDL learner, which are however exponentially worse than for Bayesian prediction. We demonstrate that these bounds are sharp, even for model classes containing only Bernoulli distributions. We show how these bounds imply regret bounds for arbitrary loss functions. Our results apply to a wide range of setups, namely sequence prediction, pattern classification, regression, and universal induction in the sense of Algorithmic Information Theory among others.

Adaptive Online Prediction by Following the Perturbed Leader

When applying aggregating strategies to Prediction with Expert Advice, the learning rate must be adaptively tuned. The natural choice of sqrt(complexity/current loss) renders the analysis of Weighted Majority derivatives quite complicated. In particular, for arbitrary weights there have been no results proven so far. The analysis of the alternative "Follow the Perturbed Leader" (FPL) algorithm from Kalai & Vempala (2003) (based on Hannan's algorithm) is easier. We derive loss bounds for adaptive learning rate and both finite expert classes with uniform weights and countable expert classes with arbitrary weights. For the former setup, our loss bounds match the best known results so far, while for the latter our results are new.

Strong Asymptotic Assertions for Discrete MDL in Regression and Classification

We study the properties of the MDL (or maximum penalized complexity) estimator for Regression and Classification, where the underlying model class is countable. We show in particular a finite bound on the Hellinger losses under the only assumption that there is a "true" model contained in the class. This implies almost sure convergence of the predictive distribution to the true one at a fast rate. It corresponds to Solomonoff's central theorem of universal induction, however with a bound that is exponentially larger.

Master Algorithms for Active Experts Problems based on Increasing Loss Values

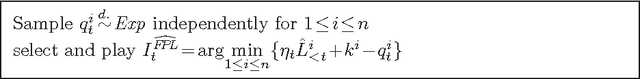
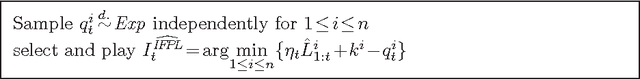
We specify an experts algorithm with the following characteristics: (a) it uses only feedback from the actions actually chosen (bandit setup), (b) it can be applied with countably infinite expert classes, and (c) it copes with losses that may grow in time appropriately slowly. We prove loss bounds against an adaptive adversary. From this, we obtain master algorithms for "active experts problems", which means that the master's actions may influence the behavior of the adversary. Our algorithm can significantly outperform standard experts algorithms on such problems. Finally, we combine it with a universal expert class. This results in a (computationally infeasible) universal master algorithm which performs - in a certain sense - almost as well as any computable strategy, for any online problem.

On the Convergence Speed of MDL Predictions for Bernoulli Sequences

We consider the Minimum Description Length principle for online sequence prediction. If the underlying model class is discrete, then the total expected square loss is a particularly interesting performance measure: (a) this quantity is bounded, implying convergence with probability one, and (b) it additionally specifies a `rate of convergence'. Generally, for MDL only exponential loss bounds hold, as opposed to the linear bounds for a Bayes mixture. We show that this is even the case if the model class contains only Bernoulli distributions. We derive a new upper bound on the prediction error for countable Bernoulli classes. This implies a small bound (comparable to the one for Bayes mixtures) for certain important model classes. The results apply to many Machine Learning tasks including classification and hypothesis testing. We provide arguments that our theorems generalize to countable classes of i.i.d. models.