MDL Convergence Speed for Bernoulli Sequences

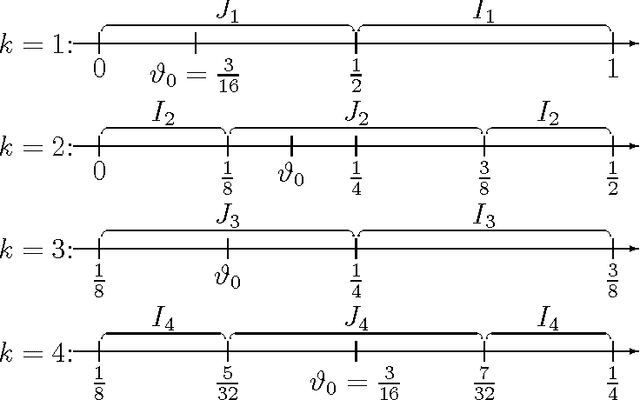
The Minimum Description Length principle for online sequence estimation/prediction in a proper learning setup is studied. If the underlying model class is discrete, then the total expected square loss is a particularly interesting performance measure: (a) this quantity is finitely bounded, implying convergence with probability one, and (b) it additionally specifies the convergence speed. For MDL, in general one can only have loss bounds which are finite but exponentially larger than those for Bayes mixtures. We show that this is even the case if the model class contains only Bernoulli distributions. We derive a new upper bound on the prediction error for countable Bernoulli classes. This implies a small bound (comparable to the one for Bayes mixtures) for certain important model classes. We discuss the application to Machine Learning tasks such as classification and hypothesis testing, and generalization to countable classes of i.i.d. models.

Robust Inference of Trees

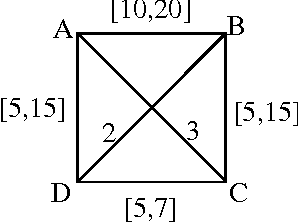
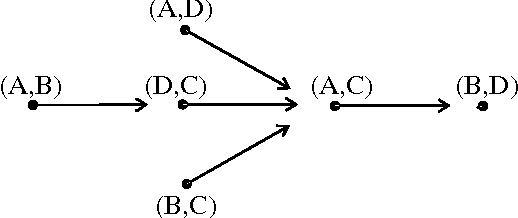
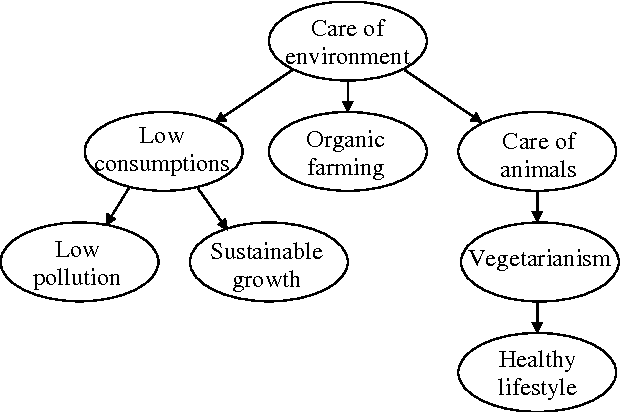
This paper is concerned with the reliable inference of optimal tree-approximations to the dependency structure of an unknown distribution generating data. The traditional approach to the problem measures the dependency strength between random variables by the index called mutual information. In this paper reliability is achieved by Walley's imprecise Dirichlet model, which generalizes Bayesian learning with Dirichlet priors. Adopting the imprecise Dirichlet model results in posterior interval expectation for mutual information, and in a set of plausible trees consistent with the data. Reliable inference about the actual tree is achieved by focusing on the substructure common to all the plausible trees. We develop an exact algorithm that infers the substructure in time O(m^4), m being the number of random variables. The new algorithm is applied to a set of data sampled from a known distribution. The method is shown to reliably infer edges of the actual tree even when the data are very scarce, unlike the traditional approach. Finally, we provide lower and upper credibility limits for mutual information under the imprecise Dirichlet model. These enable the previous developments to be extended to a full inferential method for trees.

Universal Learning of Repeated Matrix Games

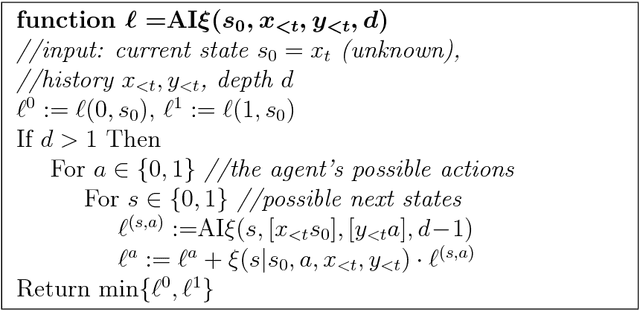
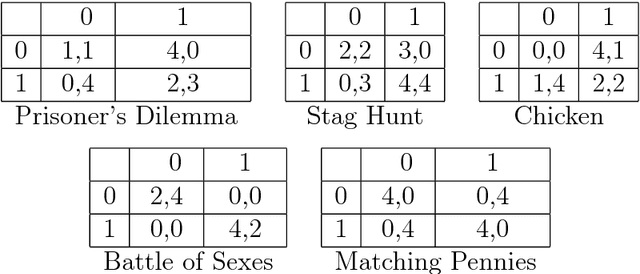
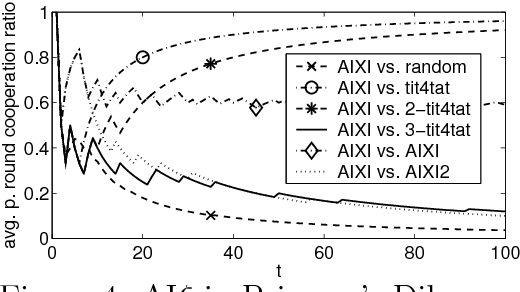
We study and compare the learning dynamics of two universal learning algorithms, one based on Bayesian learning and the other on prediction with expert advice. Both approaches have strong asymptotic performance guarantees. When confronted with the task of finding good long-term strategies in repeated 2x2 matrix games, they behave quite differently.

Sequential Predictions based on Algorithmic Complexity

This paper studies sequence prediction based on the monotone Kolmogorov complexity Km=-log m, i.e. based on universal deterministic/one-part MDL. m is extremely close to Solomonoff's universal prior M, the latter being an excellent predictor in deterministic as well as probabilistic environments, where performance is measured in terms of convergence of posteriors or losses. Despite this closeness to M, it is difficult to assess the prediction quality of m, since little is known about the closeness of their posteriors, which are the important quantities for prediction. We show that for deterministic computable environments, the "posterior" and losses of m converge, but rapid convergence could only be shown on-sequence; the off-sequence convergence can be slow. In probabilistic environments, neither the posterior nor the losses converge, in general.

Defensive Universal Learning with Experts

This paper shows how universal learning can be achieved with expert advice. To this aim, we specify an experts algorithm with the following characteristics: (a) it uses only feedback from the actions actually chosen (bandit setup), (b) it can be applied with countably infinite expert classes, and (c) it copes with losses that may grow in time appropriately slowly. We prove loss bounds against an adaptive adversary. From this, we obtain a master algorithm for "reactive" experts problems, which means that the master's actions may influence the behavior of the adversary. Our algorithm can significantly outperform standard experts algorithms on such problems. Finally, we combine it with a universal expert class. The resulting universal learner performs -- in a certain sense -- almost as well as any computable strategy, for any online decision problem. We also specify the (worst-case) convergence speed, which is very slow.

Monotone Conditional Complexity Bounds on Future Prediction Errors

We bound the future loss when predicting any (computably) stochastic sequence online. Solomonoff finitely bounded the total deviation of his universal predictor M from the true distribution m by the algorithmic complexity of m. Here we assume we are at a time t>1 and already observed x=x_1...x_t. We bound the future prediction performance on x_{t+1}x_{t+2}... by a new variant of algorithmic complexity of m given x, plus the complexity of the randomness deficiency of x. The new complexity is monotone in its condition in the sense that this complexity can only decrease if the condition is prolonged. We also briefly discuss potential generalizations to Bayesian model classes and to classification problems.

Asymptotics of Discrete MDL for Online Prediction

Minimum Description Length (MDL) is an important principle for induction and prediction, with strong relations to optimal Bayesian learning. This paper deals with learning non-i.i.d. processes by means of two-part MDL, where the underlying model class is countable. We consider the online learning framework, i.e. observations come in one by one, and the predictor is allowed to update his state of mind after each time step. We identify two ways of predicting by MDL for this setup, namely a static} and a dynamic one. (A third variant, hybrid MDL, will turn out inferior.) We will prove that under the only assumption that the data is generated by a distribution contained in the model class, the MDL predictions converge to the true values almost surely. This is accomplished by proving finite bounds on the quadratic, the Hellinger, and the Kullback-Leibler loss of the MDL learner, which are however exponentially worse than for Bayesian prediction. We demonstrate that these bounds are sharp, even for model classes containing only Bernoulli distributions. We show how these bounds imply regret bounds for arbitrary loss functions. Our results apply to a wide range of setups, namely sequence prediction, pattern classification, regression, and universal induction in the sense of Algorithmic Information Theory among others.

Adaptive Online Prediction by Following the Perturbed Leader

When applying aggregating strategies to Prediction with Expert Advice, the learning rate must be adaptively tuned. The natural choice of sqrt(complexity/current loss) renders the analysis of Weighted Majority derivatives quite complicated. In particular, for arbitrary weights there have been no results proven so far. The analysis of the alternative "Follow the Perturbed Leader" (FPL) algorithm from Kalai & Vempala (2003) (based on Hannan's algorithm) is easier. We derive loss bounds for adaptive learning rate and both finite expert classes with uniform weights and countable expert classes with arbitrary weights. For the former setup, our loss bounds match the best known results so far, while for the latter our results are new.

Fitness Uniform Deletion: A Simple Way to Preserve Diversity

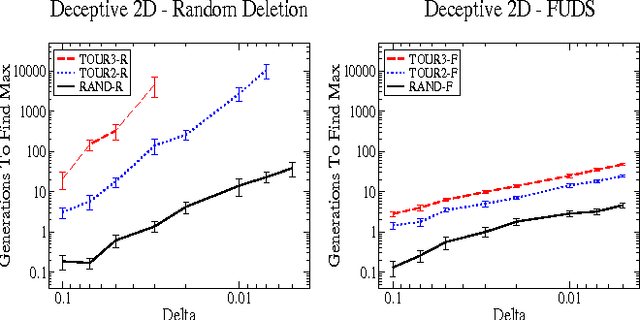
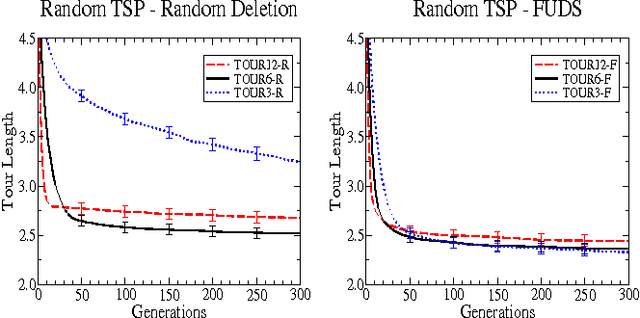
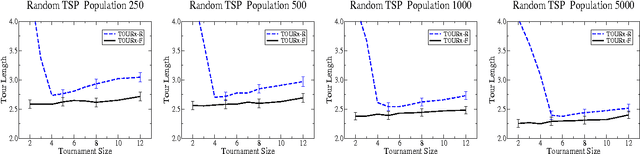
A commonly experienced problem with population based optimisation methods is the gradual decline in population diversity that tends to occur over time. This can slow a system's progress or even halt it completely if the population converges on a local optimum from which it cannot escape. In this paper we present the Fitness Uniform Deletion Scheme (FUDS), a simple but somewhat unconventional approach to this problem. Under FUDS the deletion operation is modified to only delete those individuals which are "common" in the sense that there exist many other individuals of similar fitness in the population. This makes it impossible for the population to collapse to a collection of highly related individuals with similar fitness. Our experimental results on a range of optimisation problems confirm this, in particular for deceptive optimisation problems the performance is significantly more robust to variation in the selection intensity.

On Generalized Computable Universal Priors and their Convergence

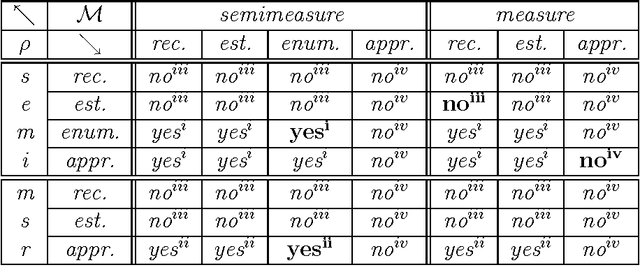
Solomonoff unified Occam's razor and Epicurus' principle of multiple explanations to one elegant, formal, universal theory of inductive inference, which initiated the field of algorithmic information theory. His central result is that the posterior of the universal semimeasure M converges rapidly to the true sequence generating posterior mu, if the latter is computable. Hence, M is eligible as a universal predictor in case of unknown mu. The first part of the paper investigates the existence and convergence of computable universal (semi)measures for a hierarchy of computability classes: recursive, estimable, enumerable, and approximable. For instance, M is known to be enumerable, but not estimable, and to dominate all enumerable semimeasures. We present proofs for discrete and continuous semimeasures. The second part investigates more closely the types of convergence, possibly implied by universality: in difference and in ratio, with probability 1, in mean sum, and for Martin-Loef random sequences. We introduce a generalized concept of randomness for individual sequences and use it to exhibit difficulties regarding these issues. In particular, we show that convergence fails (holds) on generalized-random sequences in gappy (dense) Bernoulli classes.