Manfred Jaeger
AAU
Rethinking GNNs and Missing Features: Challenges, Evaluation and a Robust Solution
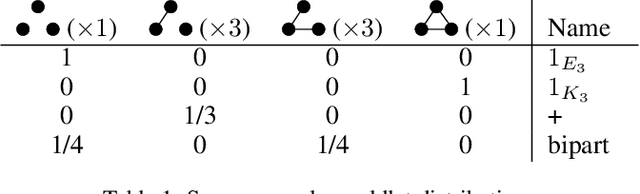
Jan 08, 2026Abstract:Handling missing node features is a key challenge for deploying Graph Neural Networks (GNNs) in real-world domains such as healthcare and sensor networks. Existing studies mostly address relatively benign scenarios, namely benchmark datasets with (a) high-dimensional but sparse node features and (b) incomplete data generated under Missing Completely At Random (MCAR) mechanisms. For (a), we theoretically prove that high sparsity substantially limits the information loss caused by missingness, making all models appear robust and preventing a meaningful comparison of their performance. To overcome this limitation, we introduce one synthetic and three real-world datasets with dense, semantically meaningful features. For (b), we move beyond MCAR and design evaluation protocols with more realistic missingness mechanisms. Moreover, we provide a theoretical background to state explicit assumptions on the missingness process and analyze their implications for different methods. Building on this analysis, we propose GNNmim, a simple yet effective baseline for node classification with incomplete feature data. Experiments show that GNNmim is competitive with respect to specialized architectures across diverse datasets and missingness regimes.
A Neuro-Symbolic Approach for Probabilistic Reasoning on Graph Data
Jul 29, 2025Abstract:Graph neural networks (GNNs) excel at predictive tasks on graph-structured data but often lack the ability to incorporate symbolic domain knowledge and perform general reasoning. Relational Bayesian Networks (RBNs), in contrast, enable fully generative probabilistic modeling over graph-like structures and support rich symbolic knowledge and probabilistic inference. This paper presents a neuro-symbolic framework that seamlessly integrates GNNs into RBNs, combining the learning strength of GNNs with the flexible reasoning capabilities of RBNs. We develop two implementations of this integration: one compiles GNNs directly into the native RBN language, while the other maintains the GNN as an external component. Both approaches preserve the semantics and computational properties of GNNs while fully aligning with the RBN modeling paradigm. We also propose a maximum a-posteriori (MAP) inference method for these neuro-symbolic models. To demonstrate the framework's versatility, we apply it to two distinct problems. First, we transform a GNN for node classification into a collective classification model that explicitly models homo- and heterophilic label patterns, substantially improving accuracy. Second, we introduce a multi-objective network optimization problem in environmental planning, where MAP inference supports complex decision-making. Both applications include new publicly available benchmark datasets. This work introduces a powerful and coherent neuro-symbolic approach to graph data, bridging learning and reasoning in ways that enable novel applications and improved performance across diverse tasks.
A Self-Explainable Heterogeneous GNN for Relational Deep Learning
Nov 30, 2024



Abstract:Recently, significant attention has been given to the idea of viewing relational databases as heterogeneous graphs, enabling the application of graph neural network (GNN) technology for predictive tasks. However, existing GNN methods struggle with the complexity of the heterogeneous graphs induced by databases with numerous tables and relations. Traditional approaches either consider all possible relational meta-paths, thus failing to scale with the number of relations, or rely on domain experts to identify relevant meta-paths. A recent solution does manage to learn informative meta-paths without expert supervision, but assumes that a node's class depends solely on the existence of a meta-path occurrence. In this work, we present a self-explainable heterogeneous GNN for relational data, that supports models in which class membership depends on aggregate information obtained from multiple occurrences of a meta-path. Experimental results show that in the context of relational databases, our approach effectively identifies informative meta-paths that faithfully capture the model's reasoning mechanisms. It significantly outperforms existing methods in both synthetic and real-world scenario.
Meta-Path Learning for Multi-relational Graph Neural Networks
Sep 29, 2023



Abstract:Existing multi-relational graph neural networks use one of two strategies for identifying informative relations: either they reduce this problem to low-level weight learning, or they rely on handcrafted chains of relational dependencies, called meta-paths. However, the former approach faces challenges in the presence of many relations (e.g., knowledge graphs), while the latter requires substantial domain expertise to identify relevant meta-paths. In this work we propose a novel approach to learn meta-paths and meta-path GNNs that are highly accurate based on a small number of informative meta-paths. Key element of our approach is a scoring function for measuring the potential informativeness of a relation in the incremental construction of the meta-path. Our experimental evaluation shows that the approach manages to correctly identify relevant meta-paths even with a large number of relations, and substantially outperforms existing multi-relational GNNs on synthetic and real-world experiments.
Learning Aggregation Functions
Dec 15, 2020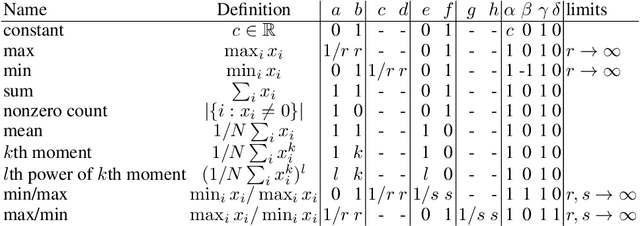
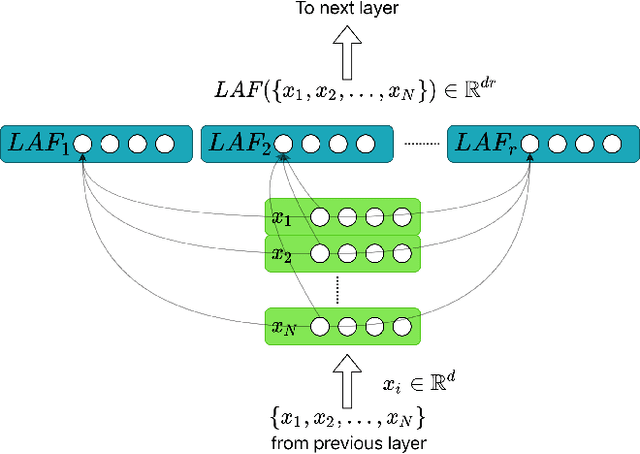

Abstract:Learning on sets is increasingly gaining attention in the machine learning community, due to its widespread applicability. Typically, representations over sets are computed by using fixed aggregation functions such as sum or maximum. However, recent results showed that universal function representation by sum- (or max-) decomposition requires either highly discontinuous (and thus poorly learnable) mappings, or a latent dimension equal to the maximum number of elements in the set. To mitigate this problem, we introduce LAF (Learning Aggregation Functions), a learnable aggregator for sets of arbitrary cardinality. LAF can approximate several extensively used aggregators (such as average, sum, maximum) as well as more complex functions (e.g. variance and skewness). We report experiments on semi-synthetic and real data showing that LAF outperforms state-of-the-art sum- (max-) decomposition architectures such as DeepSets and library-based architectures like Principal Neighborhood Aggregation.
Approximating Euclidean by Imprecise Markov Decision Processes
Jun 26, 2020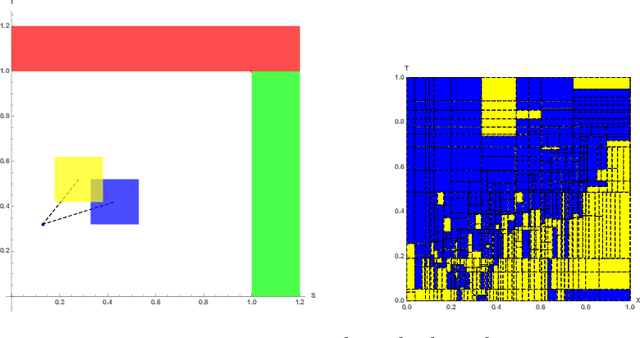
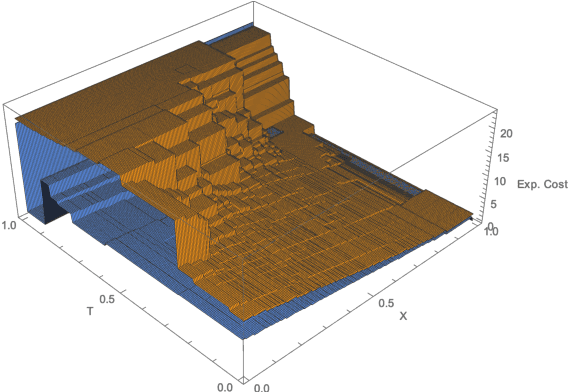
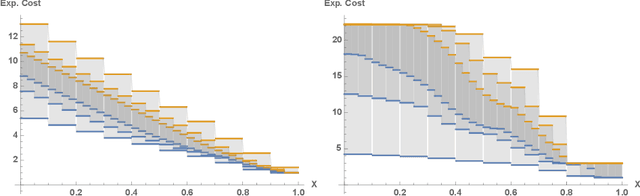
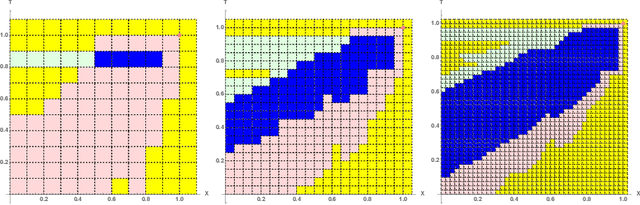
Abstract:Euclidean Markov decision processes are a powerful tool for modeling control problems under uncertainty over continuous domains. Finite state imprecise, Markov decision processes can be used to approximate the behavior of these infinite models. In this paper we address two questions: first, we investigate what kind of approximation guarantees are obtained when the Euclidean process is approximated by finite state approximations induced by increasingly fine partitions of the continuous state space. We show that for cost functions over finite time horizons the approximations become arbitrarily precise. Second, we use imprecise Markov decision process approximations as a tool to analyse and validate cost functions and strategies obtained by reinforcement learning. We find that, on the one hand, our new theoretical results validate basic design choices of a previously proposed reinforcement learning approach. On the other hand, the imprecise Markov decision process approximations reveal some inaccuracies in the learned cost functions.
A general framework for defining and optimizing robustness
Jun 19, 2020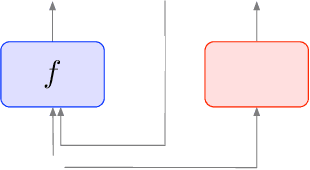
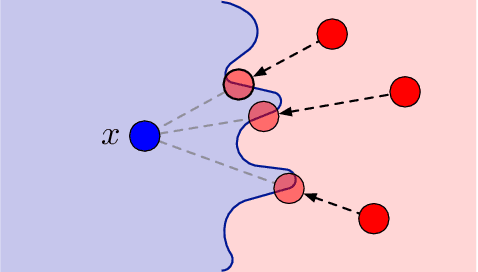
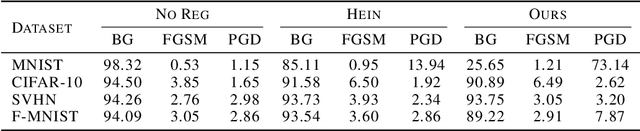
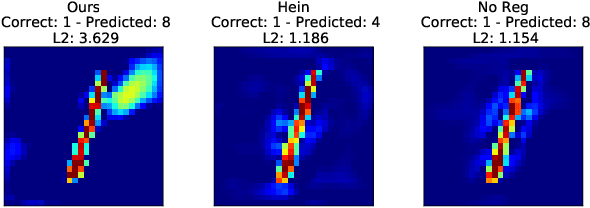
Abstract:Robustness of neural networks has recently attracted a great amount of interest. The many investigations in this area lack a precise common foundation of robustness concepts. Therefore, in this paper, we propose a rigorous and flexible framework for defining different types of robustness that also help to explain the interplay between adversarial robustness and generalization. The different robustness objectives directly lead to an adjustable family of loss functions. For two robustness concepts of particular interest we show effective ways to minimize the corresponding loss functions. One loss is designed to strengthen robustness against adversarial off-manifold attacks, and another to improve generalization under the given data distribution. Empirical results show that we can effectively train under different robustness objectives, obtaining higher robustness scores and better generalization, for the two examples respectively, compared to the state-of-the-art data augmentation and regularization techniques.
A Complete Characterization of Projectivity for Statistical Relational Models
Apr 23, 2020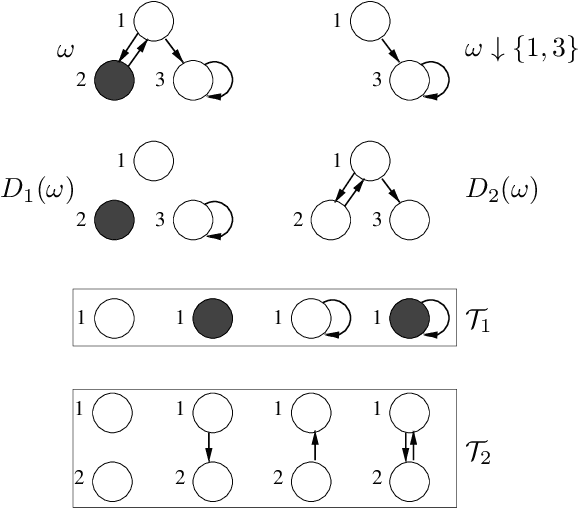
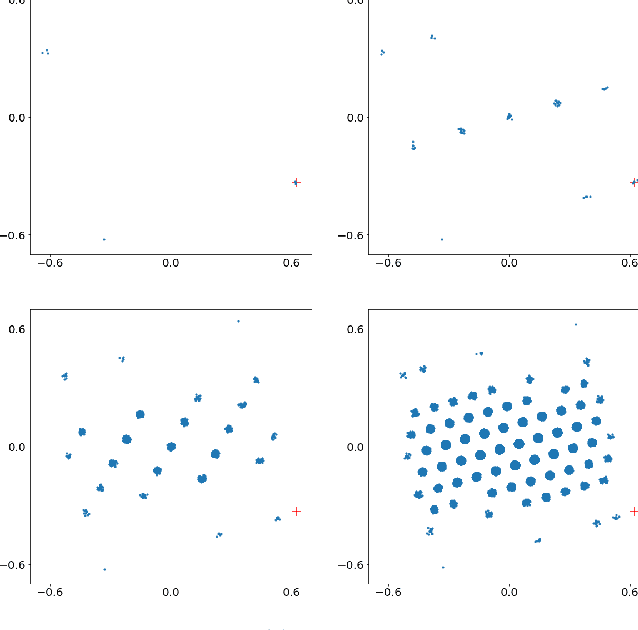
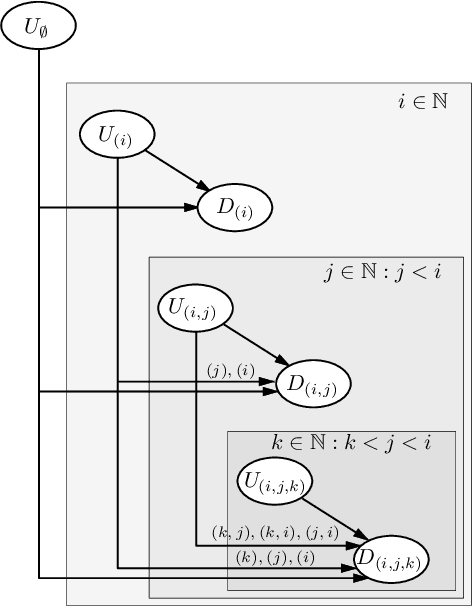
Abstract:A generative probabilistic model for relational data consists of a family of probability distributions for relational structures over domains of different sizes. In most existing statistical relational learning (SRL) frameworks, these models are not projective in the sense that the marginal of the distribution for size-$n$ structures on induced sub-structures of size $k<n$ is equal to the given distribution for size-$k$ structures. Projectivity is very beneficial in that it directly enables lifted inference and statistically consistent learning from sub-sampled relational structures. In earlier work some simple fragments of SRL languages have been identified that represent projective models. However, no complete characterization of, and representation framework for projective models has been given. In this paper we fill this gap: exploiting representation theorems for infinite exchangeable arrays we introduce a class of directed graphical latent variable models that precisely correspond to the class of projective relational models. As a by-product we also obtain a characterization for when a given distribution over size-$k$ structures is the statistical frequency distribution of size-$k$ sub-structures in much larger size-$n$ structures. These results shed new light onto the old open problem of how to apply Halpern et al.'s "random worlds approach" for probabilistic inference to general relational signatures.
Learning and Interpreting Multi-Multi-Instance Learning Networks
Oct 26, 2018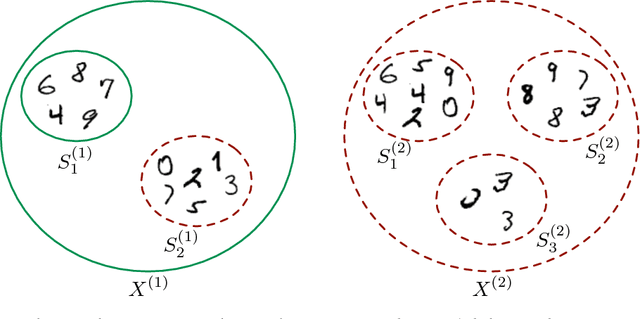
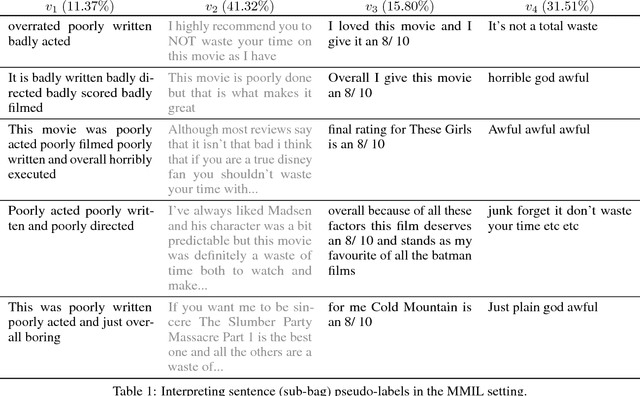
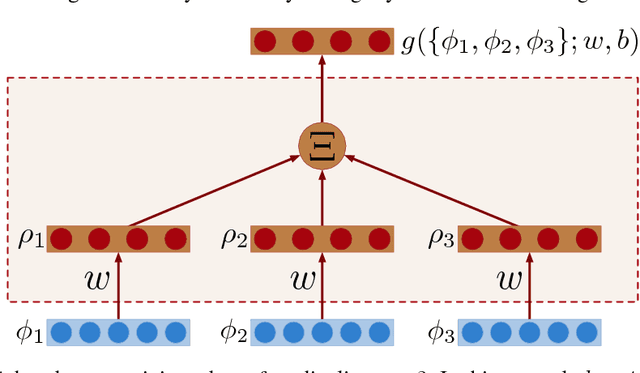
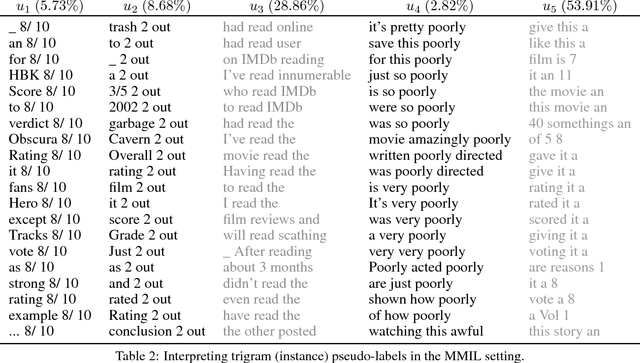
Abstract:We introduce an extension of the multi-instance learning problem where examples are organized as nested bags of instances (e.g., a document could be represented as a bag of sentences, which in turn are bags of words). This framework can be useful in various scenarios, such as text and image classification, but also supervised learning over graphs. As a further advantage, multi-multi instance learning enables a particular way of interpreting predictions and the decision function. Our approach is based on a special neural network layer, called bag-layer, whose units aggregate bags of inputs of arbitrary size. We prove theoretically that the associated class of functions contains all Boolean functions over sets of sets of instances and we provide empirical evidence that functions of this kind can be actually learned on semi-synthetic datasets. We finally present experiments on text classification and on citation graphs and social graph data, showing that our model obtains competitive results with respect to other approaches such as convolutional networks on graphs.
Inference, Learning, and Population Size: Projectivity for SRL Models
Jul 02, 2018Abstract:A subtle difference between propositional and relational data is that in many relational models, marginal probabilities depend on the population or domain size. This paper connects the dependence on population size to the classic notion of projectivity from statistical theory: Projectivity implies that relational predictions are robust with respect to changes in domain size. We discuss projectivity for a number of common SRL systems, and identify syntactic fragments that are guaranteed to yield projective models. The syntactic conditions are restrictive, which suggests that projectivity is difficult to achieve in SRL, and care must be taken when working with different domain sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge