Density based Spatial Clustering of Lines via Probabilistic Generation of Neighbourhood

Density based spatial clustering of points in $\mathbb{R}^n$ has a myriad of applications in a variety of industries. We generalise this problem to the density based clustering of lines in high-dimensional spaces, keeping in mind there exists no valid distance measure that follows the triangle inequality for lines. In this paper, we design a clustering algorithm that generates a customised neighbourhood for a line of a fixed volume (given as a parameter), based on an optional parameter as a continuous probability density function. This algorithm is not sensitive to the outliers and can effectively identify the noise in the data using a cardinality parameter. One of the pivotal applications of this algorithm is clustering data points in $\mathbb{R}^n$ with missing entries, while utilising the domain knowledge of the respective data. In particular, the proposed algorithm is able to cluster $n$-dimensional data points that contain at least $(n-1)$-dimensional information. We illustrate the neighbourhoods for the standard probability distributions with continuous probability density functions and demonstrate the effectiveness of our algorithm on various synthetic and real-world datasets (e.g., rail and road networks). The experimental results also highlight its application in clustering incomplete data.

Image Clustering without Ground Truth

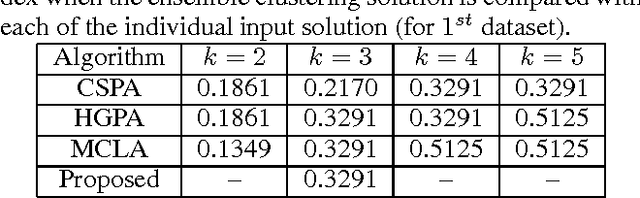
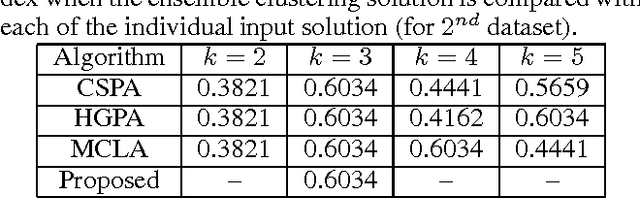
Cluster analysis has become one of the most exercised research areas over the past few decades in computer science. As a consequence, numerous clustering algorithms have already been developed to find appropriate partitions of a set of objects. Given multiple such clustering solutions, it is a challenging task to obtain an ensemble of these solutions. This becomes more challenging when the ground truth about the number of clusters is unavailable. In this paper, we introduce a crowd-powered model to collect solutions of image clustering from the general crowd and pose it as a clustering ensemble problem with variable number of clusters. The varying number of clusters basically reflects the crowd workers' perspective toward a particular set of objects. We allow a set of crowd workers to independently cluster the images as per their perceptions. We address the problem by finding out centroid of the clusters using an appropriate distance measure and prioritize the likelihood of similarity of the individual cluster sets. The effectiveness of the proposed method is demonstrated by applying it on multiple artificial datasets obtained from crowd.