Nonlinear network-based quantitative trait prediction from transcriptomic data

Quantitatively predicting phenotype variables by the expression changes in a set of candidate genes is of great interest in molecular biology but it is also a challenging task for several reasons. First, the collected biological observations might be heterogeneous and correspond to different biological mechanisms. Secondly, the gene expression variables used to predict the phenotype are potentially highly correlated since genes interact though unknown regulatory networks. In this paper, we present a novel approach designed to predict quantitative trait from transcriptomic data, taking into account the heterogeneity in biological samples and the hidden gene regulatory networks underlying different biological mechanisms. The proposed model performs well on prediction but it is also fully parametric, which facilitates the downstream biological interpretation. The model provides clusters of individuals based on the relation between gene expression data and the phenotype, and also leads to infer a gene regulatory network specific for each cluster of individuals. We perform numerical simulations to demonstrate that our model is competitive with other prediction models, and we demonstrate the predictive performance and the interpretability of our model to predict alcohol sensitivity from transcriptomic data on real data from Drosophila Melanogaster Genetic Reference Panel (DGRP).

Block-diagonal covariance selection for high-dimensional Gaussian graphical models

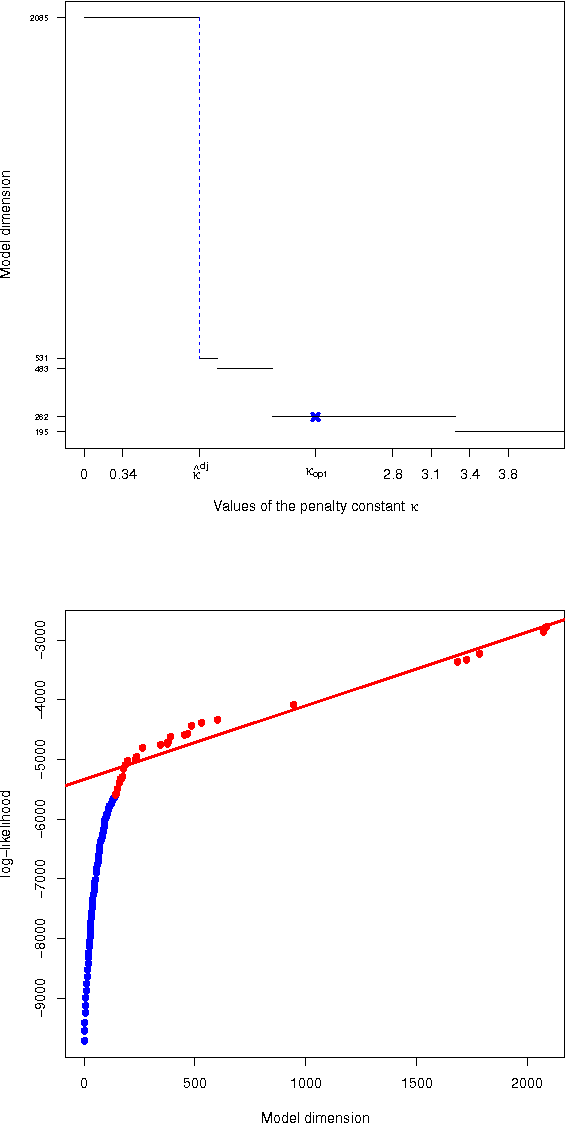
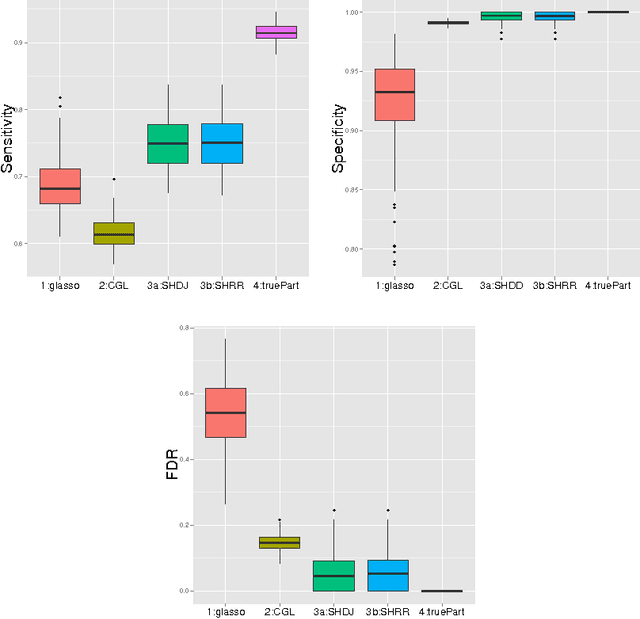
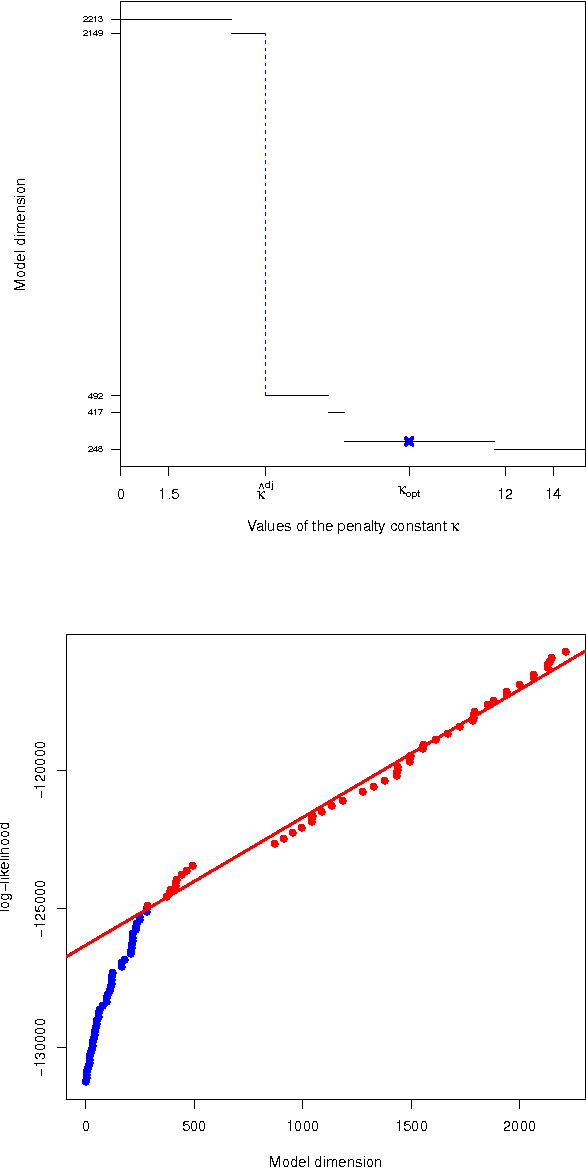
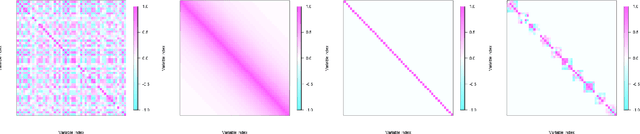
Gaussian graphical models are widely utilized to infer and visualize networks of dependencies between continuous variables. However, inferring the graph is difficult when the sample size is small compared to the number of variables. To reduce the number of parameters to estimate in the model, we propose a non-asymptotic model selection procedure supported by strong theoretical guarantees based on an oracle inequality and a minimax lower bound. The covariance matrix of the model is approximated by a block-diagonal matrix. The structure of this matrix is detected by thresholding the sample covariance matrix, where the threshold is selected using the slope heuristic. Based on the block-diagonal structure of the covariance matrix, the estimation problem is divided into several independent problems: subsequently, the network of dependencies between variables is inferred using the graphical lasso algorithm in each block. The performance of the procedure is illustrated on simulated data. An application to a real gene expression dataset with a limited sample size is also presented: the dimension reduction allows attention to be objectively focused on interactions among smaller subsets of genes, leading to a more parsimonious and interpretable modular network.