Restarted contractive operators to learn at equilibrium

Bilevel optimization offers a methodology to learn hyperparameters in imaging inverse problems, yet its integration with automatic differentiation techniques remains challenging. On the one hand, inverse problems are typically solved by iterating arbitrarily many times some elementary scheme which maps any point to the minimizer of an energy functional, known as equilibrium point. On the other hand, introducing parameters to be learned in the energy functional yield architectures very reminiscent of Neural Networks (NN) known as Unrolled NN and thus suggests the use of Automatic Differentiation (AD) techniques. Yet, applying AD requires for the NN to be of relatively small depth, thus making necessary to truncate an unrolled scheme to a finite number of iterations. First, we show that, at the minimizer, the optimal gradient descent step computed in the Deep Equilibrium (DEQ) framework admits an approximation, known as Jacobian Free Backpropagation (JFB), that is much easier to compute and can be made arbitrarily good by controlling Lipschitz properties of the truncated unrolled scheme. Second, we introduce an algorithm that combines a restart strategy with JFB computed by AD and we show that the learned steps can be made arbitrarily close to the optimal DEQ framework. Third, we complement the theoretical analysis by applying the proposed method to a variety of problems in imaging that progressively depart from the theoretical framework. In particular we show that this method is effective for training weights in weighted norms; stepsizes and regularization levels of Plug-and-Play schemes; and a DRUNet denoiser embedded in Forward-Backward iterates.

A Random Block-Coordinate Douglas-Rachford Splitting Method with Low Computational Complexity for Binary Logistic Regression

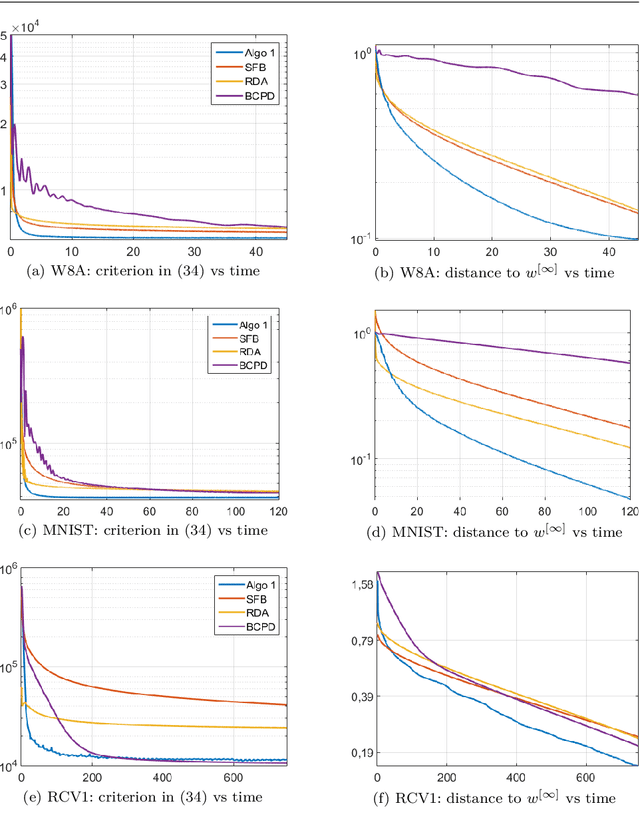
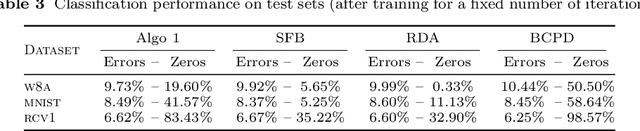
In this paper, we propose a new optimization algorithm for sparse logistic regression based on a stochastic version of the Douglas-Rachford splitting method. Our algorithm sweeps the training set by randomly selecting a mini-batch of data at each iteration, and it allows us to update the variables in a block coordinate manner. Our approach leverages the proximity operator of the logistic loss, which is expressed with the generalized Lambert W function. Experiments carried out on standard datasets demonstrate the efficiency of our approach w.r.t. stochastic gradient-like methods.

Regularization of $\ell_1$ minimization for dealing with outliers and noise in Statistics and Signal Recovery

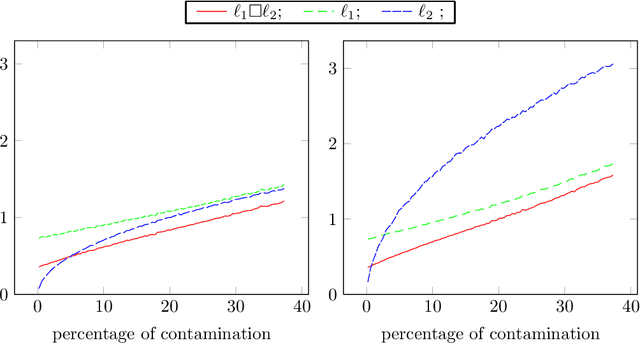
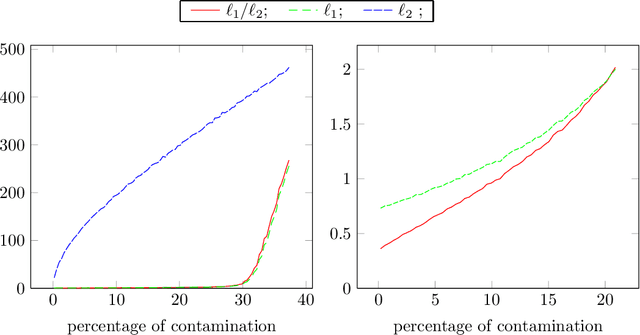
We study the robustness properties of $\ell_1$ norm minimization for the classical linear regression problem with a given design matrix and contamination restricted to the dependent variable. We perform a fine error analysis of the $\ell_1$ estimator for measurements errors consisting of outliers coupled with noise. We introduce a new estimation technique resulting from a regularization of $\ell_1$ minimization by inf-convolution with the $\ell_2$ norm. Concerning robustness to large outliers, the proposed estimator keeps the breakdown point of the $\ell_1$ estimator, and reduces to least squares when there are not outliers. We present a globally convergent forward-backward algorithm for computing our estimator and some numerical experiments confirming its theoretical properties.