Universal Coefficients and Mayer-Vietoris Sequence for Groupoid Homology

We study homology of ample groupoids via the compactly supported Moore complex of the nerve. Let $A$ be a topological abelian group. For $n\ge 0$ set $C_n(\mathcal G;A) := C_c(\mathcal G_n,A)$ and define $\partial_n^A=\sum_{i=0}^n(-1)^i(d_i)_*$. This defines $H_n(\mathcal G;A)$. The theory is functorial for continuous étale homomorphisms. It is compatible with standard reductions, including restriction to saturated clopen subsets. In the ample setting it is invariant under Kakutani equivalence. We reprove Matui type long exact sequences and identify the comparison maps at chain level. For discrete $A$ we prove a natural universal coefficient short exact sequence $$0\to H_n(\mathcal G)\otimes_{\mathbb Z}A\xrightarrow{\ ι_n^{\mathcal G}\ }H_n(\mathcal G;A)\xrightarrow{\ κ_n^{\mathcal G}\ }\operatorname{Tor}_1^{\mathbb Z}\bigl(H_{n-1}(\mathcal G),A\bigr)\to 0.$$ The key input is the chain level isomorphism $C_c(\mathcal G_n,\mathbb Z)\otimes_{\mathbb Z}A\cong C_c(\mathcal G_n,A)$, which reduces the groupoid statement to the classical algebraic UCT for the free complex $C_c(\mathcal G_\bullet,\mathbb Z)$. We also isolate the obstruction for non-discrete coefficients. For a locally compact totally disconnected Hausdorff space $X$ with a basis of compact open sets, the image of $Φ_X:C_c(X,\mathbb Z)\otimes_{\mathbb Z}A\to C_c(X,A)$ is exactly the compactly supported functions with finite image. Thus $Φ_X$ is surjective if and only if every $f\in C_c(X,A)$ has finite image, and for suitable $X$ one can produce compactly supported continuous maps $X\to A$ with infinite image. Finally, for a clopen saturated cover $\mathcal G_0=U_1\cup U_2$ we construct a short exact sequence of Moore complexes and derive a Mayer-Vietoris long exact sequence for $H_\bullet(\mathcal G;A)$ for explicit computations.

Homological Time Series Analysis of Sensor Signals from Power Plants

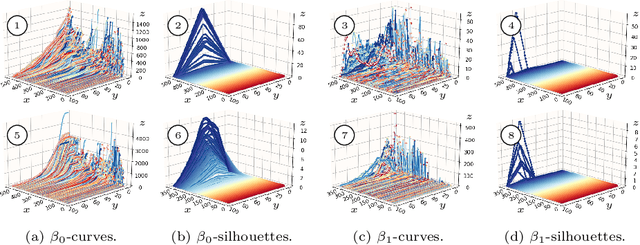
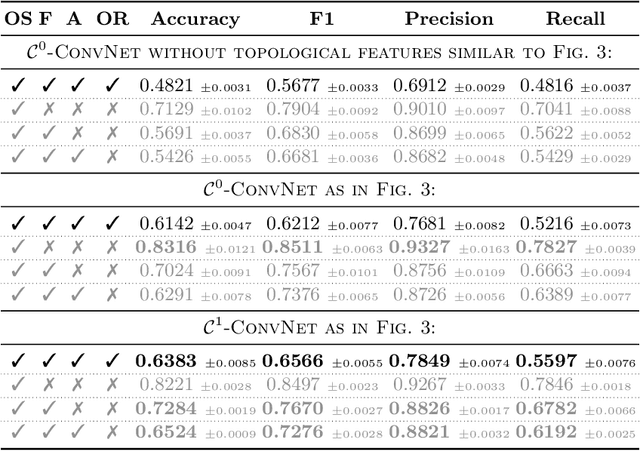
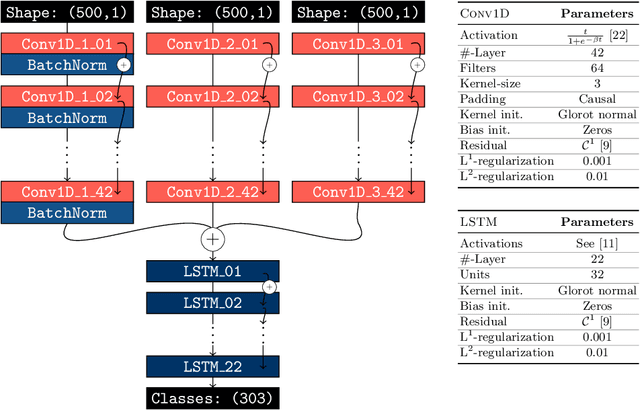
In this paper, we use topological data analysis techniques to construct a suitable neural network classifier for the task of learning sensor signals of entire power plants according to their reference designation system. We use representations of persistence diagrams to derive necessary preprocessing steps and visualize the large amounts of data. We derive architectures with deep one-dimensional convolutional layers combined with stacked long short-term memories as residual networks suitable for processing the persistence features. We combine three separate sub-networks, obtaining as input the time series itself and a representation of the persistent homology for the zeroth and first dimension. We give a mathematical derivation for most of the used hyper-parameters. For validation, numerical experiments were performed with sensor data from four power plants of the same construction type.

Parametrization of Neural Networks with Connected Abelian Lie Groups as Data Manifold

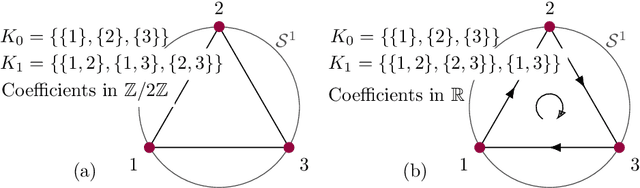
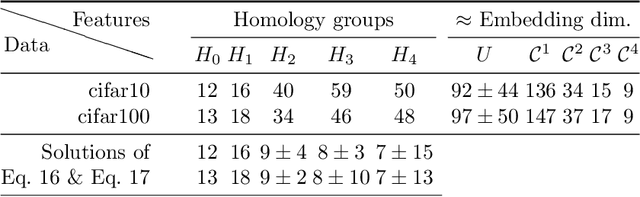
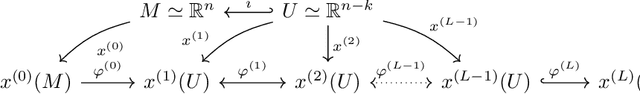
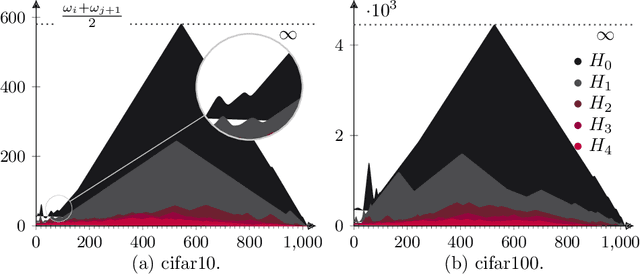
Neural nets have been used in an elusive number of scientific disciplines. Nevertheless, their parameterization is largely unexplored. Dense nets are the coordinate transformations of a manifold from which the data is sampled. After processing through a layer, the representation of the original manifold may change. This is crucial for the preservation of its topological structure and should therefore be parameterized correctly. We discuss a method to determine the smallest topology preserving layer considering the data domain as abelian connected Lie group and observe that it is decomposable into $\mathbb{R}^p \times \mathbb {T}^q$. Persistent homology allows us to count its $k$-th homology groups. Using K\"unneth's theorem, we count the $k$-th Betti numbers. Since we know the embedding dimension of $\mathbb{R}^p$ and $\mathcal{S}^1$, we parameterize the bottleneck layer with the smallest possible matrix group, which can represent a manifold with those homology groups. Resnets guarantee smaller embeddings due to the dimension of their state space representation.

Persistent Homology as Stopping-Criterion for Voronoi Interpolation

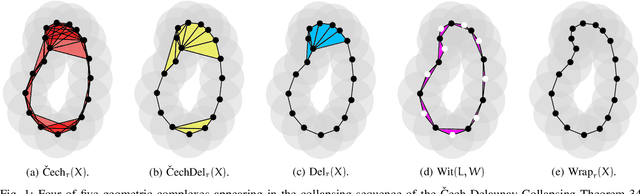
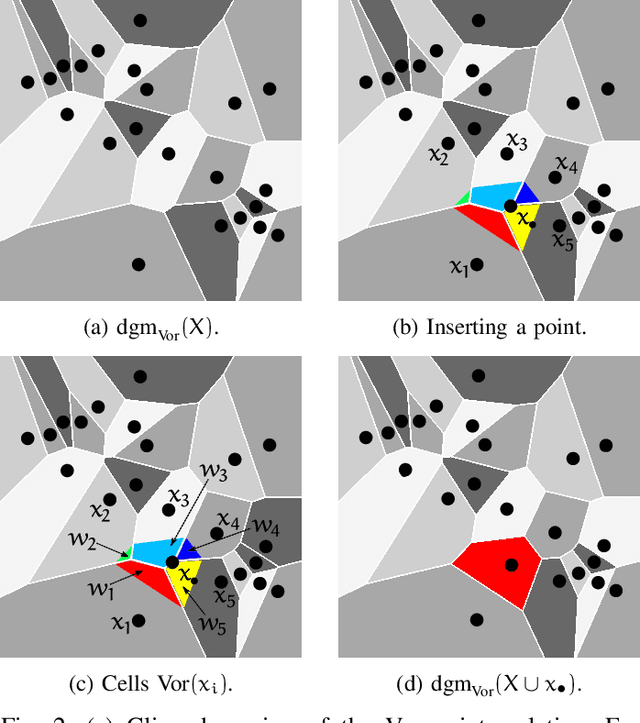
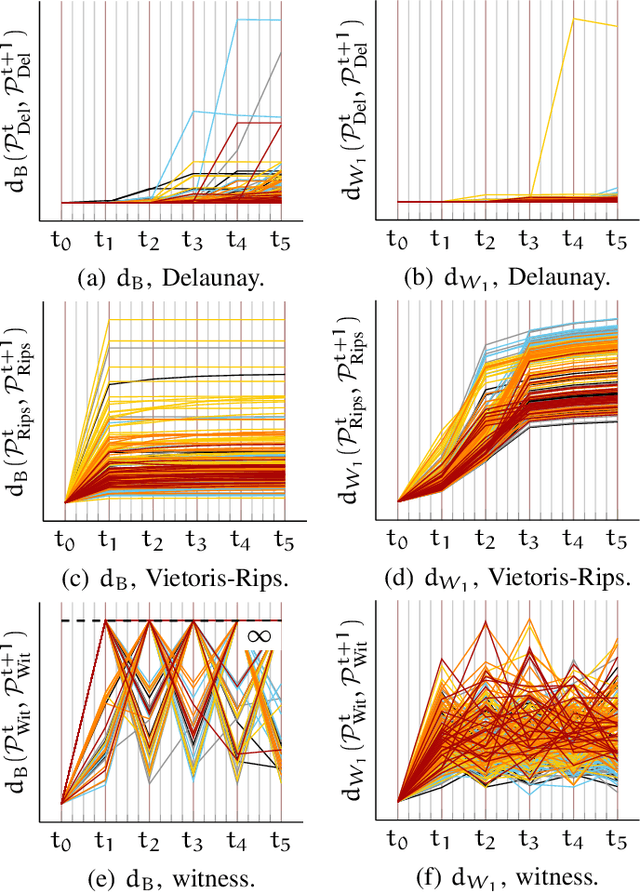
In this study the Voronoi interpolation is used to interpolate a set of points drawn from a topological space with higher homology groups on its filtration. The technique is based on Voronoi tesselation, which induces a natural dual map to the Delaunay triangulation. Advantage is taken from this fact calculating the persistent homology on it after each iteration to capture the changing topology of the data. The boundary points are identified as critical. The Bottleneck and Wasserstein distance serve as a measure of quality between the original point set and the interpolation. If the norm of two distances exceeds a heuristically determined threshold, the algorithm terminates. We give the theoretical basis for this approach and justify its validity with numerical experiments.

Deep Learning Estimation of Absorbed Dose for Nuclear Medicine Diagnostics

The distribution of energy dose from Lu$^{177}$ radiotherapy can be estimated by convolving an image of a time-integrated activity distribution with a dose voxel kernel (dvk) consisting of different types of tissues. This fast and inacurate approximation is inappropriate for personalized dosimetry as it neglects tissue heterogenity. The latter can be calculated using different imaging techniques such as CT and SPECT combined with a time consuming monte-carlo simulation. The aim of this study is, for the first time, an estimation of DVKs from CT-derived density kernels (dk) via deep learning in convolutional neural networks (cnns). The proposed cnn achieved, on the test set, a mean intersection over union (iou) of $= 0.86$ after $308$ epochs and a corresponding mean squared error (mse) $= 1.24 \cdot 10^{-4}$. This generalization ability shows that the trained cnn can indeed learn the complex transfer function from dk to dvk. Future work will evaluate dvks estimated by cnns with full monte-carlo simulations of a whole body CT to predict patient specific voxel dose maps. Keywords: Deep Learning, Nuclear Medicine, Diagnostics, Machine Learning, Statistics