Banded Matrix Operators for Gaussian Markov Models in the Automatic Differentiation Era

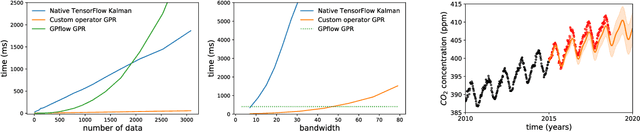
Banded matrices can be used as precision matrices in several models including linear state-space models, some Gaussian processes, and Gaussian Markov random fields. The aim of the paper is to make modern inference methods (such as variational inference or gradient-based sampling) available for Gaussian models with banded precision. We show that this can efficiently be achieved by equipping an automatic differentiation framework, such as TensorFlow or PyTorch, with some linear algebra operators dedicated to banded matrices. This paper studies the algorithmic aspects of the required operators, details their reverse-mode derivatives, and show that their complexity is linear in the number of observations.

The Complexity of Integer Bound Propagation

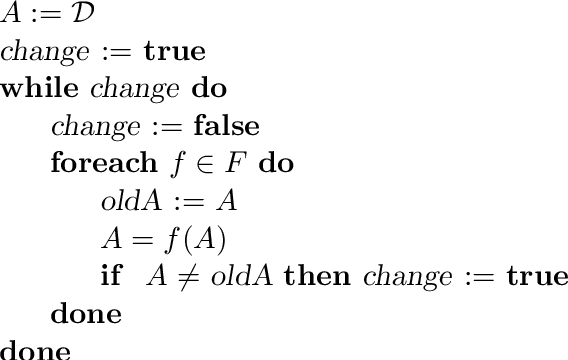
Bound propagation is an important Artificial Intelligence technique used in Constraint Programming tools to deal with numerical constraints. It is typically embedded within a search procedure ("branch and prune") and used at every node of the search tree to narrow down the search space, so it is critical that it be fast. The procedure invokes constraint propagators until a common fixpoint is reached, but the known algorithms for this have a pseudo-polynomial worst-case time complexity: they are fast indeed when the variables have a small numerical range, but they have the well-known problem of being prohibitively slow when these ranges are large. An important question is therefore whether strongly-polynomial algorithms exist that compute the common bound consistent fixpoint of a set of constraints. This paper answers this question. In particular we show that this fixpoint computation is in fact NP-complete, even when restricted to binary linear constraints.

A Unifying Framework for Structural Properties of CSPs: Definitions, Complexity, Tractability

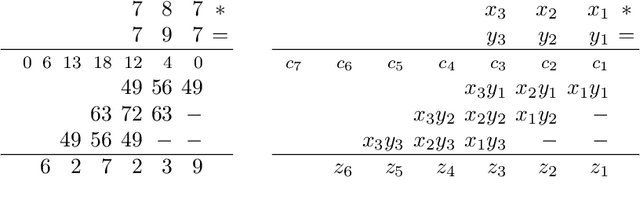
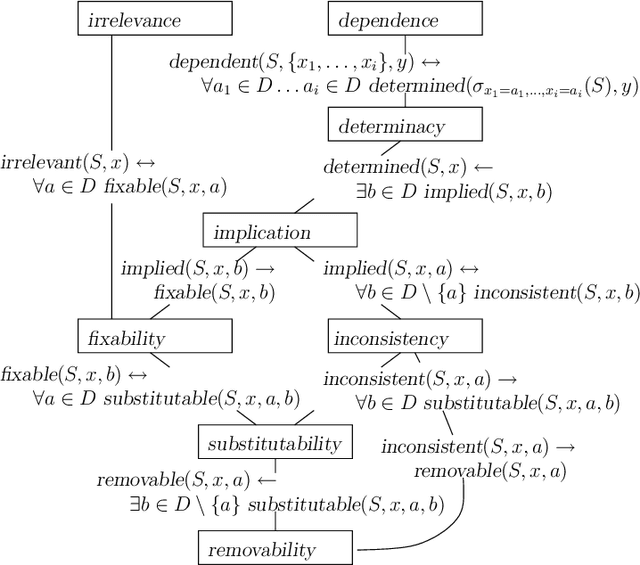
Literature on Constraint Satisfaction exhibits the definition of several structural properties that can be possessed by CSPs, like (in)consistency, substitutability or interchangeability. Current tools for constraint solving typically detect such properties efficiently by means of incomplete yet effective algorithms, and use them to reduce the search space and boost search. In this paper, we provide a unifying framework encompassing most of the properties known so far, both in CSP and other fields literature, and shed light on the semantical relationships among them. This gives a unified and comprehensive view of the topic, allows new, unknown, properties to emerge, and clarifies the computational complexity of the various detection problems. In particular, among the others, two new concepts, fixability and removability emerge, that come out to be the ideal characterisations of values that may be safely assigned or removed from a variables domain, while preserving problem satisfiability. These two notions subsume a large number of known properties, including inconsistency, substitutability and others. Because of the computational intractability of all the property-detection problems, by following the CSP approach we then determine a number of relaxations which provide sufficient conditions for their tractability. In particular, we exploit forms of language restrictions and local reasoning.

Generalizing Consistency and other Constraint Properties to Quantified Constraints

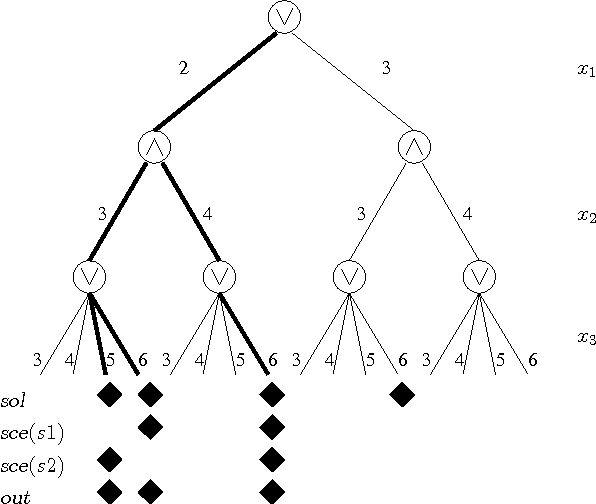
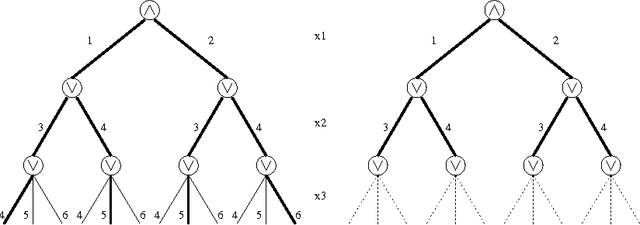
Quantified constraints and Quantified Boolean Formulae are typically much more difficult to reason with than classical constraints, because quantifier alternation makes the usual notion of solution inappropriate. As a consequence, basic properties of Constraint Satisfaction Problems (CSP), such as consistency or substitutability, are not completely understood in the quantified case. These properties are important because they are the basis of most of the reasoning methods used to solve classical (existentially quantified) constraints, and one would like to benefit from similar reasoning methods in the resolution of quantified constraints. In this paper, we show that most of the properties that are used by solvers for CSP can be generalized to quantified CSP. This requires a re-thinking of a number of basic concepts; in particular, we propose a notion of outcome that generalizes the classical notion of solution and on which all definitions are based. We propose a systematic study of the relations which hold between these properties, as well as complexity results regarding the decision of these properties. Finally, and since these problems are typically intractable, we generalize the approach used in CSP and propose weaker, easier to check notions based on locality, which allow to detect these properties incompletely but in polynomial time.