On the Role of Memory in Robust Opinion Dynamics

We investigate opinion dynamics in a fully-connected system, consisting of $n$ identical and anonymous agents, where one of the opinions (which is called correct) represents a piece of information to disseminate. In more detail, one source agent initially holds the correct opinion and remains with this opinion throughout the execution. The goal for non-source agents is to quickly agree on this correct opinion, and do that robustly, i.e., from any initial configuration. The system evolves in rounds. In each round, one agent chosen uniformly at random is activated: unless it is the source, the agent pulls the opinions of $\ell$ random agents and then updates its opinion according to some rule. We consider a restricted setting, in which agents have no memory and they only revise their opinions on the basis of those of the agents they currently sample. As restricted as it is, this setting encompasses very popular opinion dynamics, such as the voter model and best-of-$k$ majority rules. Qualitatively speaking, we show that lack of memory prevents efficient convergence. Specifically, we prove that no dynamics can achieve correct convergence in an expected number of steps that is sub-quadratic in $n$, even under a strong version of the model in which activated agents have complete access to the current configuration of the entire system, i.e., the case $\ell=n$. Conversely, we prove that the simple voter model (in which $\ell=1$) correctly solves the problem, while almost matching the aforementioned lower bound. These results suggest that, in contrast to symmetric consensus problems (that do not involve a notion of correct opinion), fast convergence on the correct opinion using stochastic opinion dynamics may indeed require the use of memory. This insight may reflect on natural information dissemination processes that rely on a few knowledgeable individuals.

On the Multidimensional Random Subset Sum Problem

In the Random Subset Sum Problem, given $n$ i.i.d. random variables $X_1, ..., X_n$, we wish to approximate any point $z \in [-1,1]$ as the sum of a suitable subset $X_{i_1(z)}, ..., X_{i_s(z)}$ of them, up to error $\varepsilon$. Despite its simple statement, this problem is of fundamental interest to both theoretical computer science and statistical mechanics. More recently, it gained renewed attention for its implications in the theory of Artificial Neural Networks. An obvious multidimensional generalisation of the problem is to consider $n$ i.i.d.\ $d$-dimensional random vectors, with the objective of approximating every point $\mathbf{z} \in [-1,1]^d$. Rather surprisingly, after Lueker's 1998 proof that, in the one-dimensional setting, $n=O(\log \frac 1\varepsilon)$ samples guarantee the approximation property with high probability, little progress has been made on achieving the above generalisation. In this work, we prove that, in $d$ dimensions, $n = O(d^3\log \frac 1\varepsilon \cdot (\log \frac 1\varepsilon + \log d))$ samples suffice for the approximation property to hold with high probability. As an application highlighting the potential interest of this result, we prove that a recently proposed neural network model exhibits \emph{universality}: with high probability, the model can approximate any neural network within a polynomial overhead in the number of parameters.

A Ihara-Bass Formula for Non-Boolean Matrices and Strong Refutations of Random CSPs

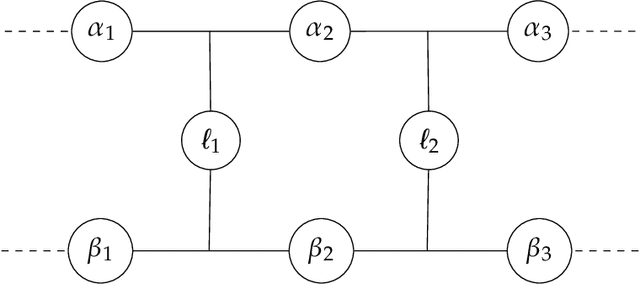
We define a notion of "non-backtracking" matrix associated to any symmetric matrix, and we prove a "Ihara-Bass" type formula for it. Previously, these notions were known only for symmetric 0/1 matrices. We use this theory to prove new results on polynomial-time strong refutations of random constraint satisfaction problems with $k$ variables per constraints (k-CSPs). For a random k-CSP instance constructed out of a constraint that is satisfied by a $p$ fraction of assignments, if the instance contains $n$ variables and $n^{k/2} / \epsilon^2$ constraints, we can efficiently compute a certificate that the optimum satisfies at most a $p+O_k(\epsilon)$ fraction of constraints. Previously, this was known for even $k$, but for odd $k$ one needed $n^{k/2} (\log n)^{O(1)} / \epsilon^2$ random constraints to achieve the same conclusion. Although the improvement is only polylogarithmic, it overcomes a significant barrier to these types of results. Strong refutation results based on current approaches construct a certificate that a certain matrix associated to the k-CSP instance is quasirandom. Such certificate can come from a Feige-Ofek type argument, from an application of Grothendieck's inequality, or from a spectral bound obtained with a trace argument. The first two approaches require a union bound that cannot work when the number of constraints is $o(n^{\lceil k/2 \rceil})$ and the third one cannot work when the number of constraints is $o(n^{k/2} \sqrt{\log n})$.

Correlation Clustering Reconstruction in Semi-Adversarial Models

Correlation Clustering is an important clustering problem with many applications. We study the reconstruction version of this problem in which one is seeking to reconstruct a latent clustering that has been corrupted by random noise and adversarial modifications. Concerning the latter, we study a standard "post-adversarial" model, in which adversarial modifications come after the noise, and also introduce and analyze a "pre-adversarial" model in which adversarial modifications come before the noise. Given an input coming from such a semi-adversarial generative model, the goal is to reconstruct almost perfectly and with high probability the latent clustering. We focus on the case where the hidden clusters have equal size and show the following. In the pre-adversarial setting, spectral algorithms are optimal, in the sense that they reconstruct all the way to the information-theoretic threshold beyond which no reconstruction is possible. In contrast, in the post-adversarial setting their ability to restore the hidden clusters stops before the threshold, but the gap is optimally filled by SDP-based algorithms.

Partitioning into Expanders

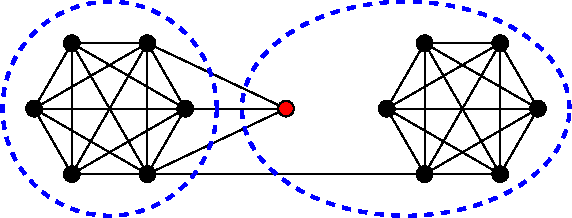
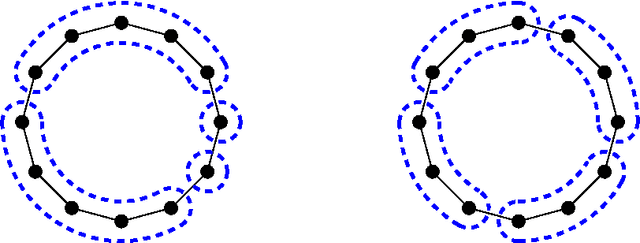
Let G=(V,E) be an undirected graph, lambda_k be the k-th smallest eigenvalue of the normalized laplacian matrix of G. There is a basic fact in algebraic graph theory that lambda_k > 0 if and only if G has at most k-1 connected components. We prove a robust version of this fact. If lambda_k>0, then for some 1\leq \ell\leq k-1, V can be {\em partitioned} into l sets P_1,\ldots,P_l such that each P_i is a low-conductance set in G and induces a high conductance induced subgraph. In particular, \phi(P_i)=O(l^3\sqrt{\lambda_l}) and \phi(G[P_i]) >= \lambda_k/k^2). We make our results algorithmic by designing a simple polynomial time spectral algorithm to find such partitioning of G with a quadratic loss in the inside conductance of P_i's. Unlike the recent results on higher order Cheeger's inequality [LOT12,LRTV12], our algorithmic results do not use higher order eigenfunctions of G. If there is a sufficiently large gap between lambda_k and lambda_{k+1}, more precisely, if \lambda_{k+1} >= \poly(k) lambda_{k}^{1/4} then our algorithm finds a k partitioning of V into sets P_1,...,P_k such that the induced subgraph G[P_i] has a significantly larger conductance than the conductance of P_i in G. Such a partitioning may represent the best k clustering of G. Our algorithm is a simple local search that only uses the Spectral Partitioning algorithm as a subroutine. We expect to see further applications of this simple algorithm in clustering applications.

Improved Cheeger's Inequality: Analysis of Spectral Partitioning Algorithms through Higher Order Spectral Gap

Let \phi(G) be the minimum conductance of an undirected graph G, and let 0=\lambda_1 <= \lambda_2 <=... <= \lambda_n <= 2 be the eigenvalues of the normalized Laplacian matrix of G. We prove that for any graph G and any k >= 2, \phi(G) = O(k) \lambda_2 / \sqrt{\lambda_k}, and this performance guarantee is achieved by the spectral partitioning algorithm. This improves Cheeger's inequality, and the bound is optimal up to a constant factor for any k. Our result shows that the spectral partitioning algorithm is a constant factor approximation algorithm for finding a sparse cut if \lambda_k$ is a constant for some constant k. This provides some theoretical justification to its empirical performance in image segmentation and clustering problems. We extend the analysis to other graph partitioning problems, including multi-way partition, balanced separator, and maximum cut.