PICT -- A Differentiable, GPU-Accelerated Multi-Block PISO Solver for Simulation-Coupled Learning Tasks in Fluid Dynamics

Despite decades of advancements, the simulation of fluids remains one of the most challenging areas of in scientific computing. Supported by the necessity of gradient information in deep learning, differentiable simulators have emerged as an effective tool for optimization and learning in physics simulations. In this work, we present our fluid simulator PICT, a differentiable pressure-implicit solver coded in PyTorch with Graphics-processing-unit (GPU) support. We first verify the accuracy of both the forward simulation and our derived gradients in various established benchmarks like lid-driven cavities and turbulent channel flows before we show that the gradients provided by our solver can be used to learn complicated turbulence models in 2D and 3D. We apply both supervised and unsupervised training regimes using physical priors to match flow statistics. In particular, we learn a stable sub-grid scale (SGS) model for a 3D turbulent channel flow purely based on reference statistics. The low-resolution corrector trained with our solver runs substantially faster than the highly resolved references, while keeping or even surpassing their accuracy. Finally, we give additional insights into the physical interpretation of different solver gradients, and motivate a physically informed regularization technique. To ensure that the full potential of PICT can be leveraged, it is published as open source: https://github.com/tum-pbs/PICT.

Predicting the temporal dynamics of turbulent channels through deep learning

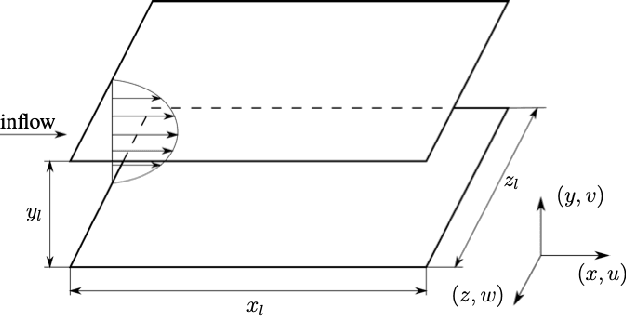
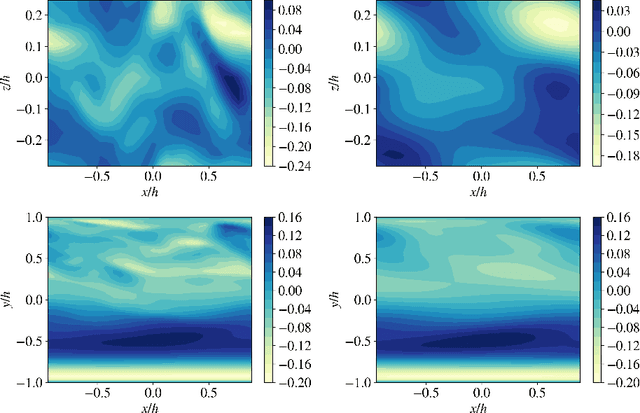
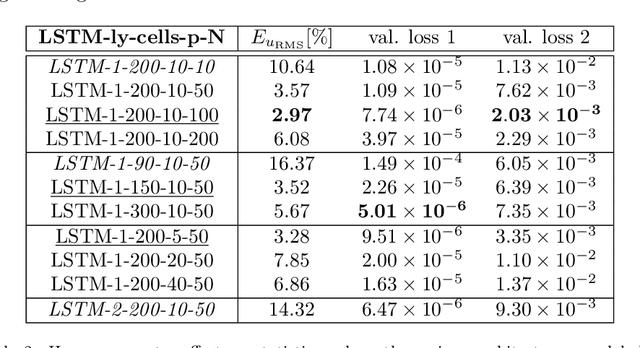
The success of recurrent neural networks (RNNs) has been demonstrated in many applications related to turbulence, including flow control, optimization, turbulent features reproduction as well as turbulence prediction and modeling. With this study we aim to assess the capability of these networks to reproduce the temporal evolution of a minimal turbulent channel flow. We first obtain a data-driven model based on a modal decomposition in the Fourier domain (which we denote as FFT-POD) of the time series sampled from the flow. This particular case of turbulent flow allows us to accurately simulate the most relevant coherent structures close to the wall. Long-short-term-memory (LSTM) networks and a Koopman-based framework (KNF) are trained to predict the temporal dynamics of the minimal-channel-flow modes. Tests with different configurations highlight the limits of the KNF method compared to the LSTM, given the complexity of the flow under study. Long-term prediction for LSTM show excellent agreement from the statistical point of view, with errors below 2% for the best models with respect to the reference. Furthermore, the analysis of the chaotic behaviour through the use of the Lyapunov exponents and of the dynamic behaviour through Poincar\'e maps emphasizes the ability of the LSTM to reproduce the temporal dynamics of turbulence. Alternative reduced-order models (ROMs), based on the identification of different turbulent structures, are explored and they continue to show a good potential in predicting the temporal dynamics of the minimal channel.

Recurrent neural networks and Koopman-based frameworks for temporal predictions in turbulence

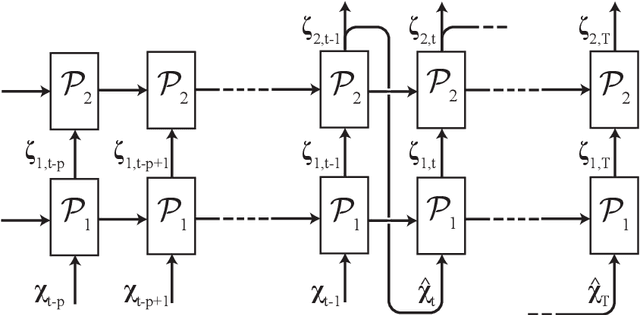
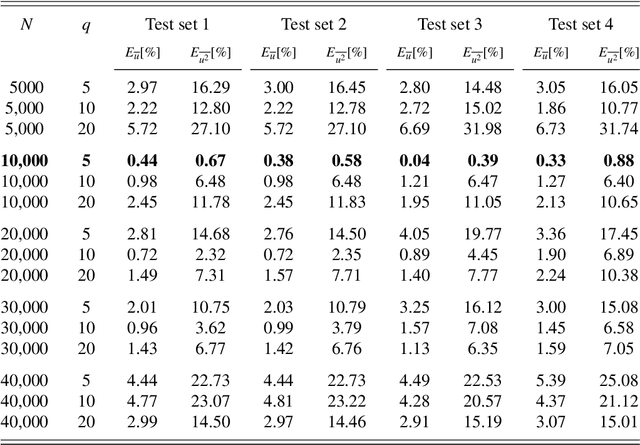
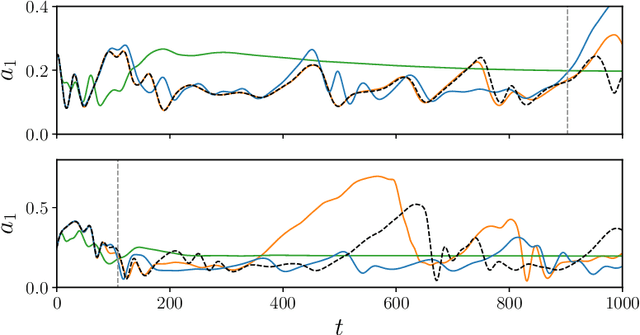
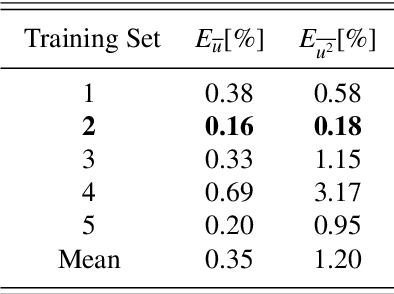
The prediction capabilities of recurrent neural networks and Koopman-based frameworks are assessed in the low-order model of near-wall turbulence by Moehlis et al. (New J. Phys. 6, 56, 2004). Our results show that it is possible to obtain excellent predictions of the turbulence statistics and the dynamic behavior of the flow with properly trained long-short-term memory (LSTM) networks, leading to relative errors in the mean and the fluctuations below $1\%$. Besides, a newly developed Koopman-based framework, called Koopman with nonlinear forcing (KNF), leads to the same level of accuracy in the statistics at a significantly lower computational expense. Furthermore, the KNF framework outperforms the LSTM network when it comes to short-term predictions. We also observe that using a loss function based only on the instantaneous predictions of the flow can lead to suboptimal predictions in terms of turbulence statistics. Thus, we propose a stopping criterion based on the computed statistics which effectively avoids overfitting to instantaneous predictions at the cost of deteriorated statistics. This suggests that a new loss function, including the averaged behavior of the flow as well as the instantaneous predictions, may lead to an improved generalization ability of the network.

On the use of recurrent neural networks for predictions of turbulent flows

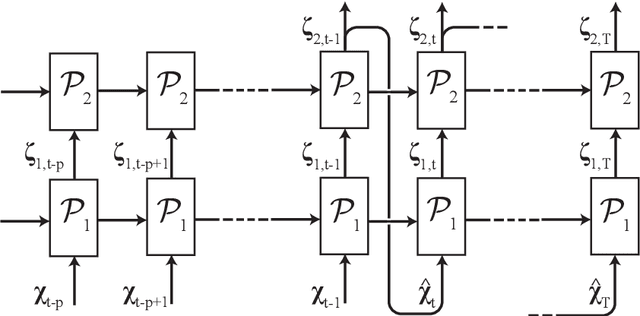
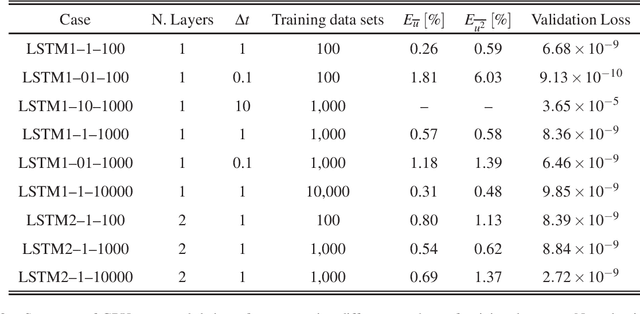
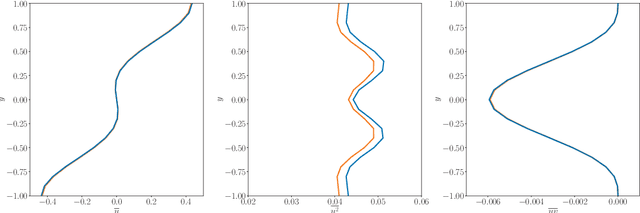
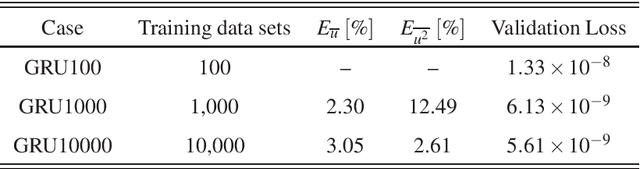
In this paper, the prediction capabilities of recurrent neural networks are assessed in the low-order model of near-wall turbulence by Moehlis {\it et al.} (New J. Phys. {\bf 6}, 56, 2004). Our results show that it is possible to obtain excellent predictions of the turbulence statistics and the dynamic behavior of the flow with properly trained long short-term memory (LSTM) networks, leading to relative errors in the mean and the fluctuations below $1\%$. We also observe that using a loss function based only on the instantaneous predictions of the flow may not lead to the best predictions in terms of turbulence statistics, and it is necessary to define a stopping criterion based on the computed statistics. Furthermore, more sophisticated loss functions, including not only the instantaneous predictions but also the averaged behavior of the flow, may lead to much faster neural network training.