ISDE : Independence Structure Density Estimation

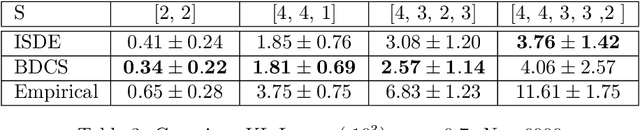
Density estimation appears as a subroutine in many learning procedures, so it is of interest to have efficient methods for it to perform in practical situations. Multidimensional density estimation suffers from the curse of dimensionality. A solution to this problem is to add a structural hypothesis through an undirected graphical model on the underlying distribution. We propose ISDE (Independence Structure Density Estimation), an algorithm designed to estimate a density and an undirected graphical model from a particular family of graphs corresponding to Independence Structure (IS), a situation where we can separate features into independent groups. ISDE works for moderately high-dimensional data (up to a few dozen features), and it is useable in parametric and nonparametric situations. Existing methods on nonparametric graphical model estimation focus on multidimensional dependencies only through pairwise ones: ISDE does not suffer from this restriction and can address structures not yet covered by available algorithms. In this paper, we present the existing theory about IS, explain the construction of our algorithm and prove its effectiveness. This is done on synthetic data both quantitatively, through measures of density estimation performance under Kullback-Leibler loss, and qualitatively, in terms of capability to recover IS. By applying ISDE on mass cytometry datasets, we also show how it performs both quantitatively and qualitatively on real-world datasets. Then we provide information about running time.

Still no free lunches: the price to pay for tighter PAC-Bayes bounds

"No free lunch" results state the impossibility of obtaining meaningful bounds on the error of a learning algorithm without prior assumptions and modelling. Some models are expensive (strong assumptions, such as as subgaussian tails), others are cheap (simply finite variance). As it is well known, the more you pay, the more you get: in other words, the most expensive models yield the more interesting bounds. Recent advances in robust statistics have investigated procedures to obtain tight bounds while keeping the cost minimal. The present paper explores and exhibits what the limits are for obtaining tight PAC-Bayes bounds in a robust setting for cheap models, addressing the question: is PAC-Bayes good value for money?