Breaking the Curse of Dimensionality in Deep Neural Networks by Learning Invariant Representations

Artificial intelligence, particularly the subfield of machine learning, has seen a paradigm shift towards data-driven models that learn from and adapt to data. This has resulted in unprecedented advancements in various domains such as natural language processing and computer vision, largely attributed to deep learning, a special class of machine learning models. Deep learning arguably surpasses traditional approaches by learning the relevant features from raw data through a series of computational layers. This thesis explores the theoretical foundations of deep learning by studying the relationship between the architecture of these models and the inherent structures found within the data they process. In particular, we ask What drives the efficacy of deep learning algorithms and allows them to beat the so-called curse of dimensionality-i.e. the difficulty of generally learning functions in high dimensions due to the exponentially increasing need for data points with increased dimensionality? Is it their ability to learn relevant representations of the data by exploiting their structure? How do different architectures exploit different data structures? In order to address these questions, we push forward the idea that the structure of the data can be effectively characterized by its invariances-i.e. aspects that are irrelevant for the task at hand. Our methodology takes an empirical approach to deep learning, combining experimental studies with physics-inspired toy models. These simplified models allow us to investigate and interpret the complex behaviors we observe in deep learning systems, offering insights into their inner workings, with the far-reaching goal of bridging the gap between theory and practice.

How Deep Neural Networks Learn Compositional Data: The Random Hierarchy Model

Learning generic high-dimensional tasks is notably hard, as it requires a number of training data exponential in the dimension. Yet, deep convolutional neural networks (CNNs) have shown remarkable success in overcoming this challenge. A popular hypothesis is that learnable tasks are highly structured and that CNNs leverage this structure to build a low-dimensional representation of the data. However, little is known about how much training data they require, and how this number depends on the data structure. This paper answers this question for a simple classification task that seeks to capture relevant aspects of real data: the Random Hierarchy Model. In this model, each of the $n_c$ classes corresponds to $m$ synonymic compositions of high-level features, which are in turn composed of sub-features through an iterative process repeated $L$ times. We find that the number of training data $P^*$ required by deep CNNs to learn this task (i) grows asymptotically as $n_c m^L$, which is only polynomial in the input dimensionality; (ii) coincides with the training set size such that the representation of a trained network becomes invariant to exchanges of synonyms; (iii) corresponds to the number of data at which the correlations between low-level features and classes become detectable. Overall, our results indicate how deep CNNs can overcome the curse of dimensionality by building invariant representations, and provide an estimate of the number of data required to learn a task based on its hierarchically compositional structure.

How deep convolutional neural networks lose spatial information with training

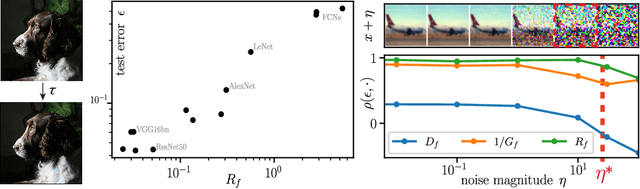
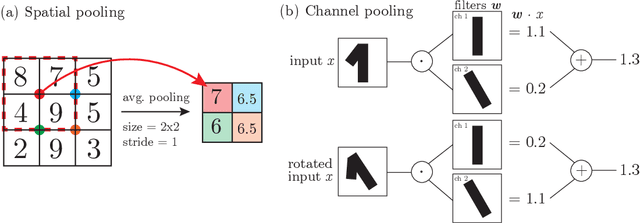
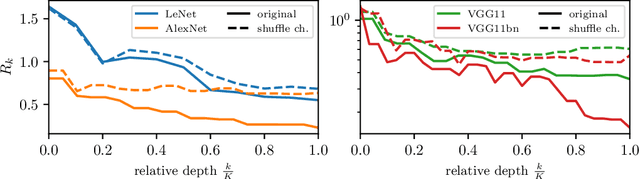
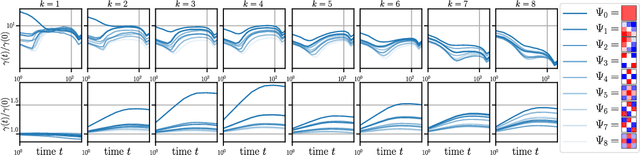
A central question of machine learning is how deep nets manage to learn tasks in high dimensions. An appealing hypothesis is that they achieve this feat by building a representation of the data where information irrelevant to the task is lost. For image datasets, this view is supported by the observation that after (and not before) training, the neural representation becomes less and less sensitive to diffeomorphisms acting on images as the signal propagates through the net. This loss of sensitivity correlates with performance, and surprisingly correlates with a gain of sensitivity to white noise acquired during training. These facts are unexplained, and as we demonstrate still hold when white noise is added to the images of the training set. Here, we (i) show empirically for various architectures that stability to image diffeomorphisms is achieved by spatial pooling in the first half of the net, and by channel pooling in the second half, (ii) introduce a scale-detection task for a simple model of data where pooling is learned during training, which captures all empirical observations above and (iii) compute in this model how stability to diffeomorphisms and noise scale with depth. The scalings are found to depend on the presence of strides in the net architecture. We find that the increased sensitivity to noise is due to the perturbing noise piling up during pooling, after being rectified by ReLU units.

Learning sparse features can lead to overfitting in neural networks

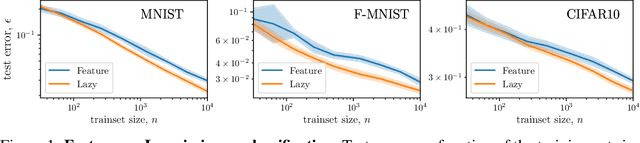
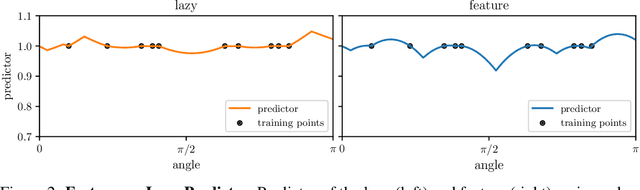
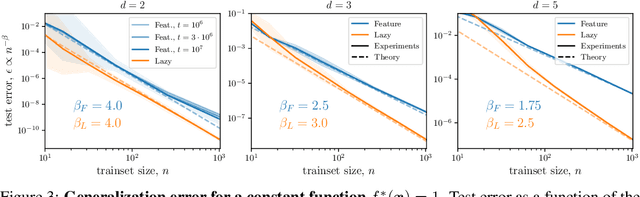
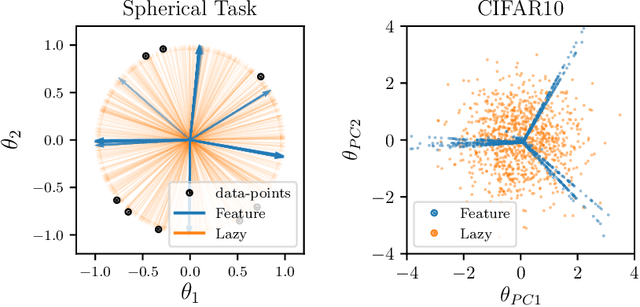
It is widely believed that the success of deep networks lies in their ability to learn a meaningful representation of the features of the data. Yet, understanding when and how this feature learning improves performance remains a challenge: for example, it is beneficial for modern architectures trained to classify images, whereas it is detrimental for fully-connected networks trained for the same task on the same data. Here we propose an explanation for this puzzle, by showing that feature learning can perform worse than lazy training (via random feature kernel or the NTK) as the former can lead to a sparser neural representation. Although sparsity is known to be essential for learning anisotropic data, it is detrimental when the target function is constant or smooth along certain directions of input space. We illustrate this phenomenon in two settings: (i) regression of Gaussian random functions on the d-dimensional unit sphere and (ii) classification of benchmark datasets of images. For (i), we compute the scaling of the generalization error with number of training points, and show that methods that do not learn features generalize better, even when the dimension of the input space is large. For (ii), we show empirically that learning features can indeed lead to sparse and thereby less smooth representations of the image predictors. This fact is plausibly responsible for deteriorating the performance, which is known to be correlated with smoothness along diffeomorphisms.

Relative stability toward diffeomorphisms in deep nets indicates performance

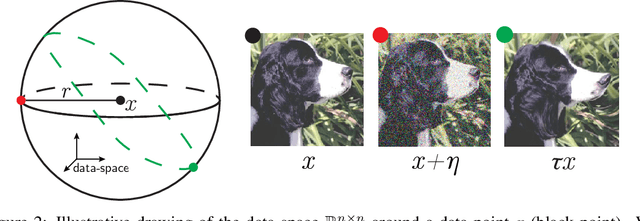
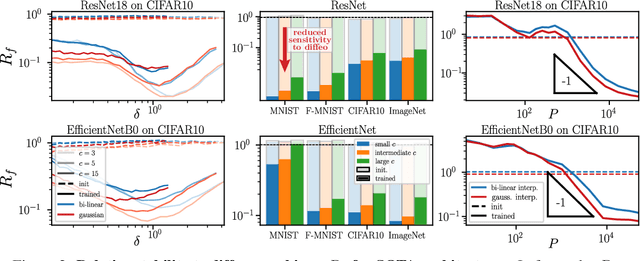
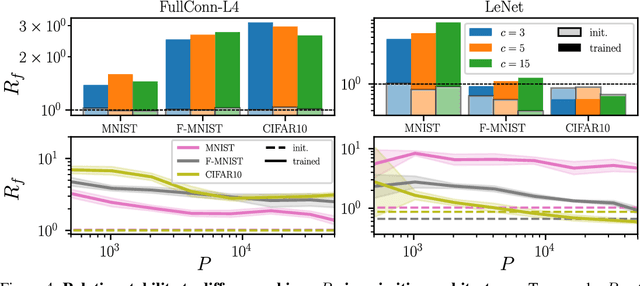
Understanding why deep nets can classify data in large dimensions remains a challenge. It has been proposed that they do so by becoming stable to diffeomorphisms, yet existing empirical measurements support that it is often not the case. We revisit this question by defining a maximum-entropy distribution on diffeomorphisms, that allows to study typical diffeomorphisms of a given norm. We confirm that stability toward diffeomorphisms does not strongly correlate to performance on four benchmark data sets of images. By contrast, we find that the stability toward diffeomorphisms relative to that of generic transformations $R_f$ correlates remarkably with the test error $\epsilon_t$. It is of order unity at initialization but decreases by several decades during training for state-of-the-art architectures. For CIFAR10 and 15 known architectures, we find $\epsilon_t\approx 0.2\sqrt{R_f}$, suggesting that obtaining a small $R_f$ is important to achieve good performance. We study how $R_f$ depends on the size of the training set and compare it to a simple model of invariant learning.

Perspective: A Phase Diagram for Deep Learning unifying Jamming, Feature Learning and Lazy Training

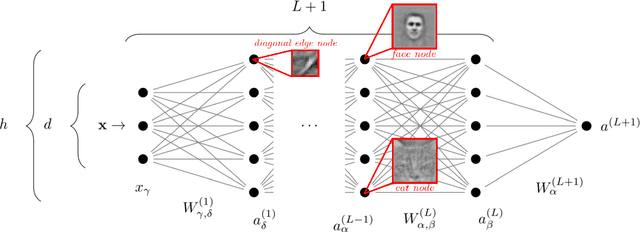
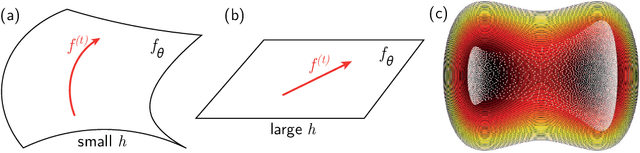
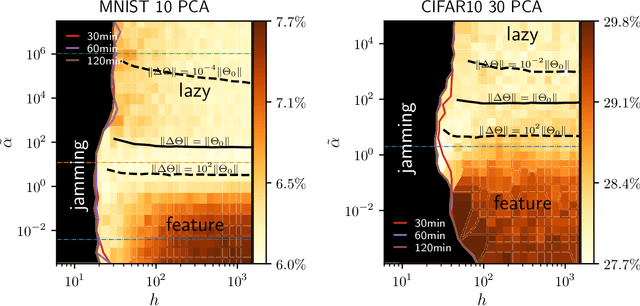
Deep learning algorithms are responsible for a technological revolution in a variety of tasks including image recognition or Go playing. Yet, why they work is not understood. Ultimately, they manage to classify data lying in high dimension -- a feat generically impossible due to the geometry of high dimensional space and the associated curse of dimensionality. Understanding what kind of structure, symmetry or invariance makes data such as images learnable is a fundamental challenge. Other puzzles include that (i) learning corresponds to minimizing a loss in high dimension, which is in general not convex and could well get stuck bad minima. (ii) Deep learning predicting power increases with the number of fitting parameters, even in a regime where data are perfectly fitted. In this manuscript, we review recent results elucidating (i,ii) and the perspective they offer on the (still unexplained) curse of dimensionality paradox. We base our theoretical discussion on the $(h,\alpha)$ plane where $h$ is the network width and $\alpha$ the scale of the output of the network at initialization, and provide new systematic measures of performance in that plane for MNIST and CIFAR 10. We argue that different learning regimes can be organized into a phase diagram. A line of critical points sharply delimits an under-parametrised phase from an over-parametrized one. In over-parametrized nets, learning can operate in two regimes separated by a smooth cross-over. At large initialization, it corresponds to a kernel method, whereas for small initializations features can be learnt, together with invariants in the data. We review the properties of these different phases, of the transition separating them and some open questions. Our treatment emphasizes analogies with physical systems, scaling arguments and the development of numerical observables to quantitatively test these results empirically.

Geometric compression of invariant manifolds in neural nets

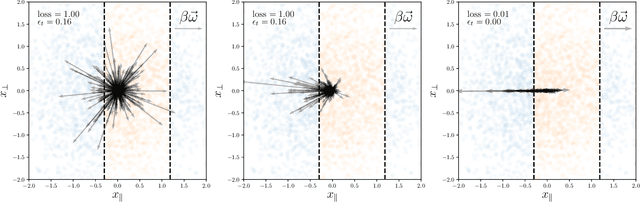
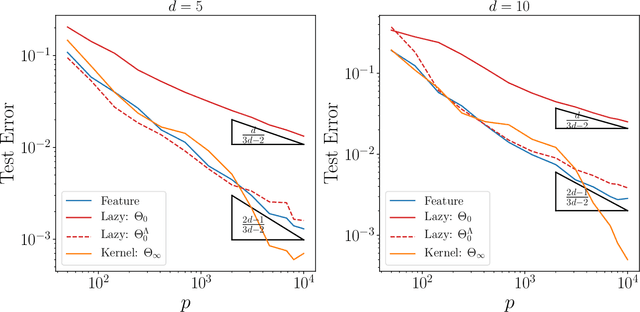
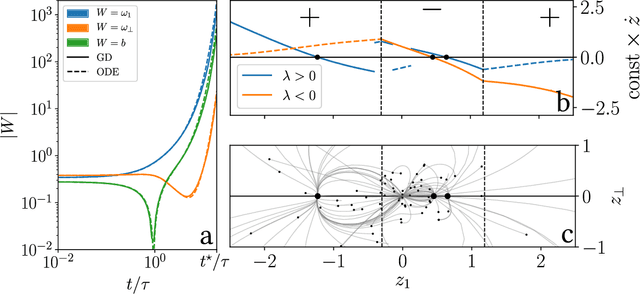
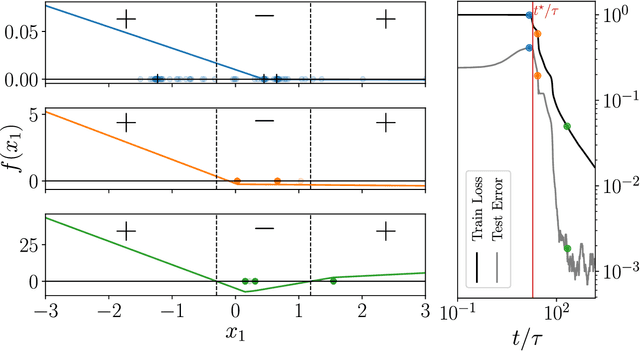
We study how neural networks compress uninformative input space in models where data lie in $d$ dimensions, but whose label only vary within a linear manifold of dimension $d_\parallel < d$. We show that for a one-hidden layer network initialized with infinitesimal weights (i.e. in the \textit{feature learning} regime) trained with gradient descent, the uninformative $d_\perp=d-d_\parallel$ space is compressed by a factor $\lambda\sim \sqrt{p}$, where $p$ is the size of the training set. We quantify the benefit of such a compression on the test error $\epsilon$. For large initialization of the weights (the \textit{lazy training} regime), no compression occurs and for regular boundaries separating labels we find that $\epsilon \sim p^{-\beta}$, with $\beta_\text{Lazy} = d / (3d-2)$. Compression improves the learning curves so that $\beta_\text{Feature} = (2d-1)/(3d-2)$ if $d_\parallel = 1$ and $\beta_\text{Feature} = (d + d_\perp/2)/(3d-2)$ if $d_\parallel > 1$. We test these predictions for a stripe model where boundaries are parallel interfaces ($d_\parallel=1$) as well as for a cylindrical boundary ($d_\parallel=2$). Next we show that compression shapes the Neural Tangent Kernel (NTK) evolution in time, so that its top eigenvectors become more informative and display a larger projection on the labels. Consequently, kernel learning with the frozen NTK at the end of training outperforms the initial NTK. We confirm these predictions both for a one-hidden layer FC network trained on the stripe model and for a 16-layers CNN trained on MNIST, for which we also find $\beta_\text{Feature}>\beta_\text{Lazy}$. The great similarities found in these two cases support that compression is central to the training of MNIST, and puts forward kernel-PCA on the evolving NTK as a useful diagnostic of compression in deep nets.