Embracing Discrete Search: A Reasonable Approach to Causal Structure Learning

We present FLOP (Fast Learning of Order and Parents), a score-based causal discovery algorithm for linear models. It pairs fast parent selection with iterative Cholesky-based score updates, cutting run-times over prior algorithms. This makes it feasible to fully embrace discrete search, enabling iterated local search with principled order initialization to find graphs with scores at or close to the global optimum. The resulting structures are highly accurate across benchmarks, with near-perfect recovery in standard settings. This performance calls for revisiting discrete search over graphs as a reasonable approach to causal discovery.

Adjustment Identification Distance: A gadjid for Causal Structure Learning

Evaluating graphs learned by causal discovery algorithms is difficult: The number of edges that differ between two graphs does not reflect how the graphs differ with respect to the identifying formulas they suggest for causal effects. We introduce a framework for developing causal distances between graphs which includes the structural intervention distance for directed acyclic graphs as a special case. We use this framework to develop improved adjustment-based distances as well as extensions to completed partially directed acyclic graphs and causal orders. We develop polynomial-time reachability algorithms to compute the distances efficiently. In our package gadjid (open source at https://github.com/CausalDisco/gadjid), we provide implementations of our distances; they are orders of magnitude faster than the structural intervention distance and thereby provide a success metric for causal discovery that scales to graph sizes that were previously prohibitive.

Exploiting Independent Instruments: Identification and Distribution Generalization

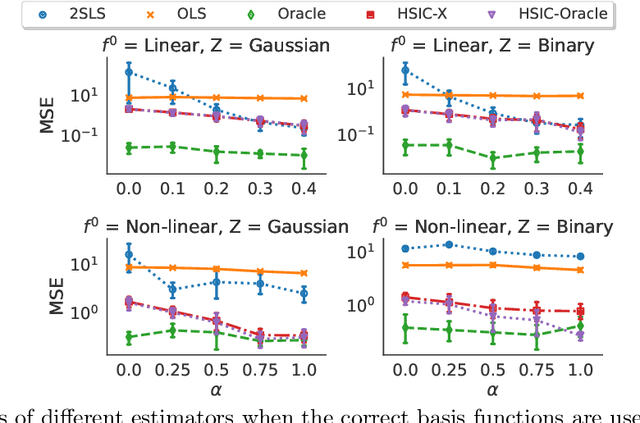
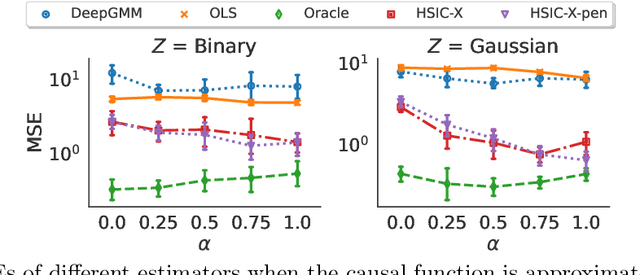
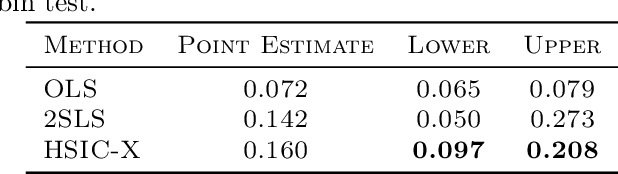
Instrumental variable models allow us to identify a causal function between covariates X and a response Y, even in the presence of unobserved confounding. Most of the existing estimators assume that the error term in the response Y and the hidden confounders are uncorrelated with the instruments Z. This is often motivated by a graphical separation, an argument that also justifies independence. Posing an independence condition, however, leads to strictly stronger identifiability results. We connect to existing literature in econometrics and provide a practical method for exploiting independence that can be combined with any gradient-based learning procedure. We see that even in identifiable settings, taking into account higher moments may yield better finite sample results. Furthermore, we exploit the independence for distribution generalization. We prove that the proposed estimator is invariant to distributional shifts on the instruments and worst-case optimal whenever these shifts are sufficiently strong. These results hold even in the under-identified case where the instruments are not sufficiently rich to identify the causal function.