Theory of coupled neuronal-synaptic dynamics

In neural circuits, synapses influence neurons by shaping network dynamics, and neurons influence synapses through activity-dependent plasticity. Motivated by this fact, we study a network model in which neurons and synapses are mutually coupled dynamic variables. Model neurons obey dynamics shaped by synaptic couplings that fluctuate, in turn, about quenched random strengths in response to pre- and postsynaptic neuronal activity. Using dynamical mean-field theory, we compute the phase diagram of the combined neuronal-synaptic system, revealing several novel phases suggestive of computational function. In the regime in which the non-plastic system is chaotic, Hebbian plasticity slows chaos, while anti-Hebbian plasticity quickens chaos and generates an oscillatory component in neuronal activity. Deriving the spectrum of the joint neuronal-synaptic Jacobian reveals that these behaviors manifest as differential effects of eigenvalue repulsion. In the regime in which the non-plastic system is quiescent, Hebbian plasticity can induce chaos. In both regimes, sufficiently strong Hebbian plasticity creates exponentially many stable neuronal-synaptic fixed points that coexist with chaotic states. Finally, in chaotic states with sufficiently strong Hebbian plasticity, halting synaptic dynamics leaves a stable fixed point of neuronal dynamics, freezing the neuronal state. This phase of freezable chaos provides a novel mechanism of synaptic working memory in which a stable fixed point of neuronal dynamics is continuously destabilized through synaptic dynamics, allowing any neuronal state to be stored as a stable fixed point by halting synaptic plasticity.

Dimension of Activity in Random Neural Networks

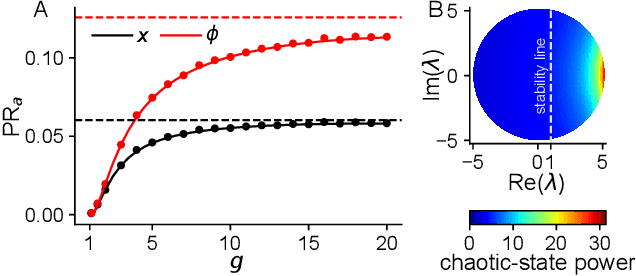
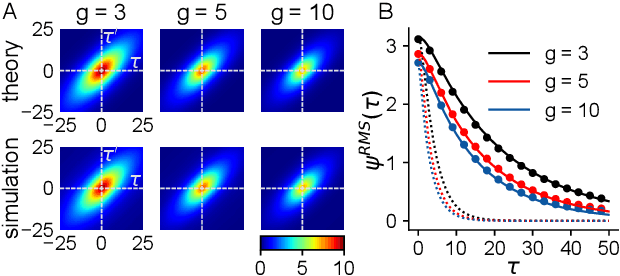
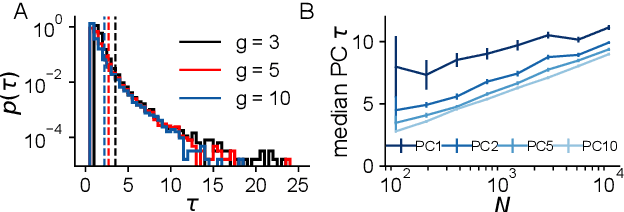
Neural networks are high-dimensional nonlinear dynamical systems that process information through the coordinated activity of many interconnected units. Understanding how biological and machine-learning networks function and learn requires knowledge of the structure of this coordinated activity, information contained in cross-covariances between units. Although dynamical mean field theory (DMFT) has elucidated several features of random neural networks -- in particular, that they can generate chaotic activity -- existing DMFT approaches do not support the calculation of cross-covariances. We solve this longstanding problem by extending the DMFT approach via a two-site cavity method. This reveals, for the first time, several spatial and temporal features of activity coordination, including the effective dimension, defined as the participation ratio of the spectrum of the covariance matrix. Our results provide a general analytical framework for studying the structure of collective activity in random neural networks and, more broadly, in high-dimensional nonlinear dynamical systems with quenched disorder.

The Implicit Bias of Gradient Descent on Generalized Gated Linear Networks

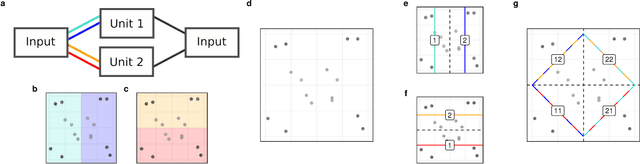
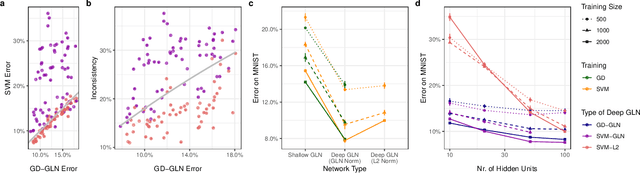
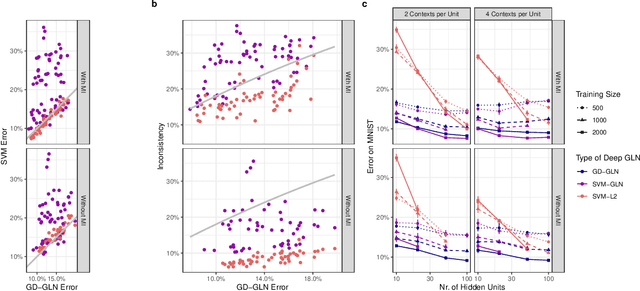
Understanding the asymptotic behavior of gradient-descent training of deep neural networks is essential for revealing inductive biases and improving network performance. We derive the infinite-time training limit of a mathematically tractable class of deep nonlinear neural networks, gated linear networks (GLNs), and generalize these results to gated networks described by general homogeneous polynomials. We study the implications of our results, focusing first on two-layer GLNs. We then apply our theoretical predictions to GLNs trained on MNIST and show how architectural constraints and the implicit bias of gradient descent affect performance. Finally, we show that our theory captures a substantial portion of the inductive bias of ReLU networks. By making the inductive bias explicit, our framework is poised to inform the development of more efficient, biologically plausible, and robust learning algorithms.

Input correlations impede suppression of chaos and learning in balanced rate networks

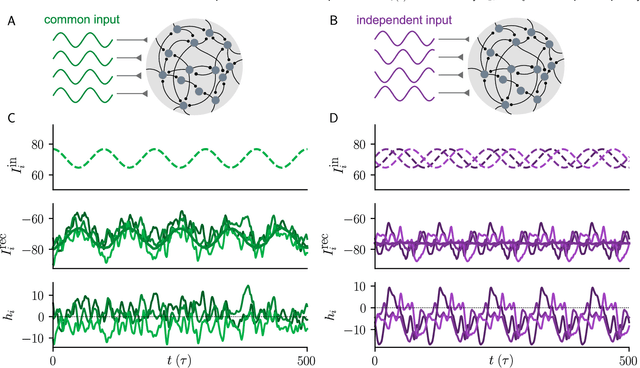
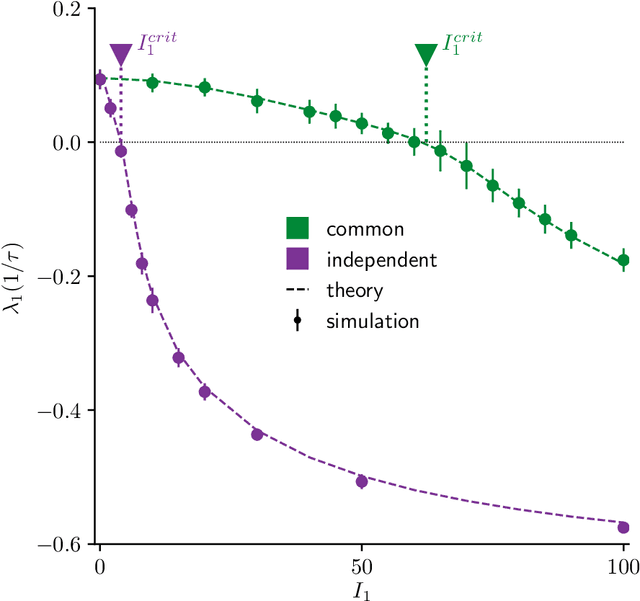
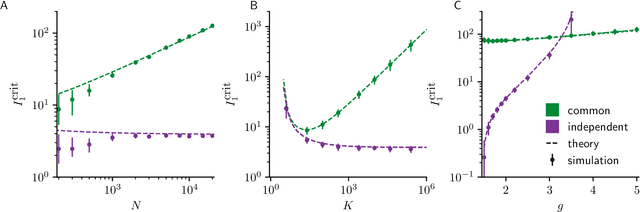
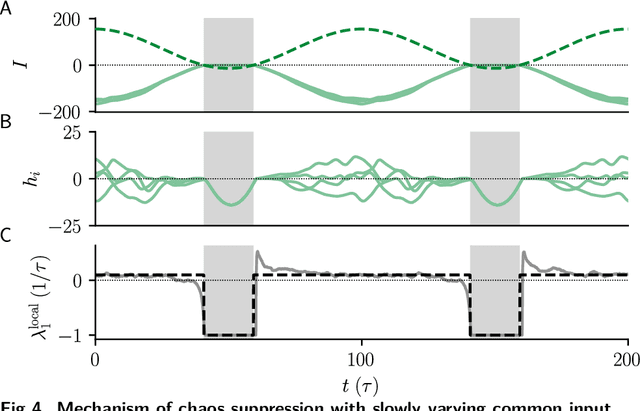
Neural circuits exhibit complex activity patterns, both spontaneously and evoked by external stimuli. Information encoding and learning in neural circuits depend on how well time-varying stimuli can control spontaneous network activity. We show that in firing-rate networks in the balanced state, external control of recurrent dynamics, i.e., the suppression of internally-generated chaotic variability, strongly depends on correlations in the input. A unique feature of balanced networks is that, because common external input is dynamically canceled by recurrent feedback, it is far easier to suppress chaos with independent inputs into each neuron than through common input. To study this phenomenon we develop a non-stationary dynamic mean-field theory that determines how the activity statistics and largest Lyapunov exponent depend on frequency and amplitude of the input, recurrent coupling strength, and network size, for both common and independent input. We also show that uncorrelated inputs facilitate learning in balanced networks.

Credit Assignment Through Broadcasting a Global Error Vector

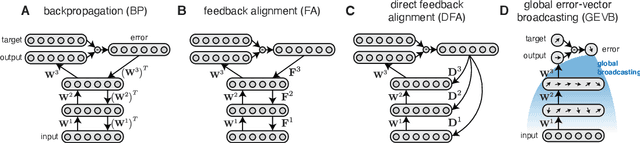
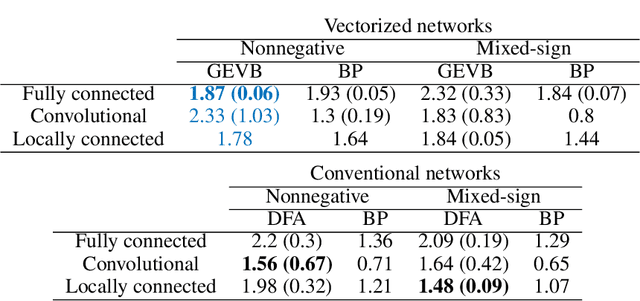
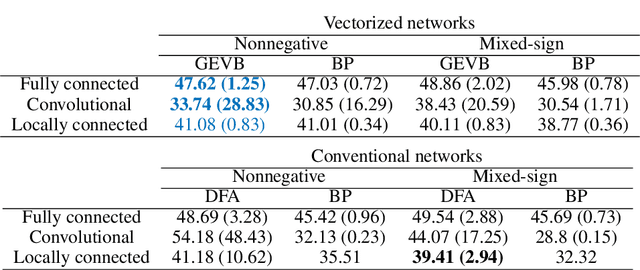
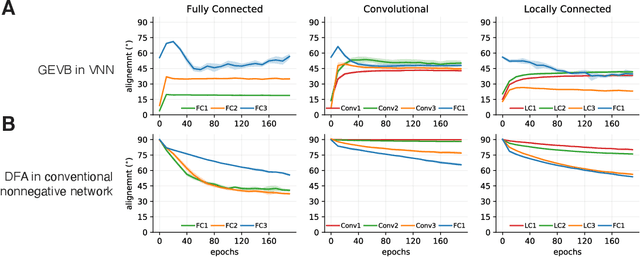
Backpropagation (BP) uses detailed, unit-specific feedback to train deep neural networks (DNNs) with remarkable success. That biological neural circuits appear to perform credit assignment, but cannot implement BP, implies the existence of other powerful learning algorithms. Here, we explore the extent to which a globally broadcast learning signal, coupled with local weight updates, enables training of DNNs. We present both a learning rule, called global error-vector broadcasting (GEVB), and a class of DNNs, called vectorized nonnegative networks (VNNs), in which this learning rule operates. VNNs have vector-valued units and nonnegative weights past the first layer. The GEVB learning rule generalizes three-factor Hebbian learning, updating each weight by an amount proportional to the inner product of the presynaptic activation and a globally broadcast error vector when the postsynaptic unit is active. We prove that these weight updates are matched in sign to the gradient, enabling accurate credit assignment. Moreover, at initialization, these updates are exactly proportional to the gradient in the limit of infinite network width. GEVB matches the performance of BP in VNNs, and in some cases outperforms direct feedback alignment (DFA) applied in conventional networks. Unlike DFA, GEVB successfully trains convolutional layers. Altogether, our theoretical and empirical results point to a surprisingly powerful role for a global learning signal in training DNNs.

Neural population geometry: An approach for understanding biological and artificial neural networks

Advances in experimental neuroscience have transformed our ability to explore the structure and function of neural circuits. At the same time, advances in machine learning have unleashed the remarkable computational power of artificial neural networks (ANNs). While these two fields have different tools and applications, they present a similar challenge: namely, understanding how information is embedded and processed through high-dimensional representations to solve complex tasks. One approach to addressing this challenge is to utilize mathematical and computational tools to analyze the geometry of these high-dimensional representations, i.e., neural population geometry. We review examples of geometrical approaches providing insight into the function of biological and artificial neural networks: representation untangling in perception, a geometric theory of classification capacity, disentanglement and abstraction in cognitive systems, topological representations underlying cognitive maps, dynamic untangling in motor systems, and a dynamical approach to cognition. Together, these findings illustrate an exciting trend at the intersection of machine learning, neuroscience, and geometry, in which neural population geometry provides a useful population-level mechanistic descriptor underlying task implementation. Importantly, geometric descriptions are applicable across sensory modalities, brain regions, network architectures and timescales. Thus, neural population geometry has the potential to unify our understanding of structure and function in biological and artificial neural networks, bridging the gap between single neurons, populations and behavior.

Training dynamically balanced excitatory-inhibitory networks

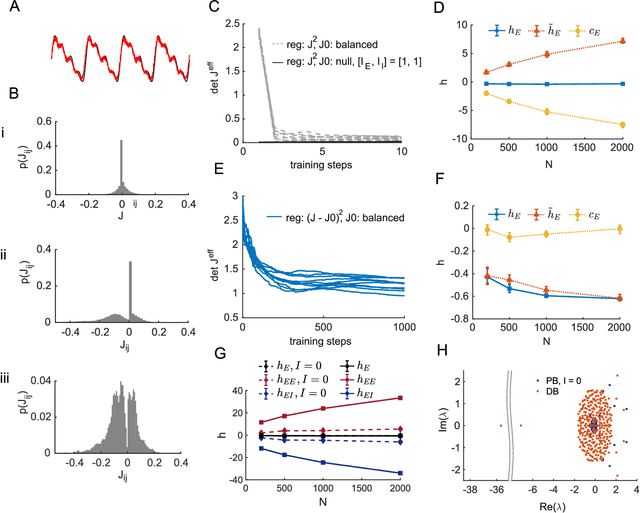
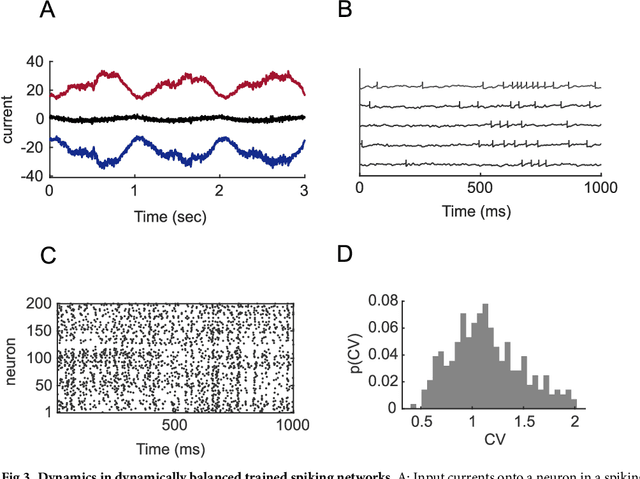
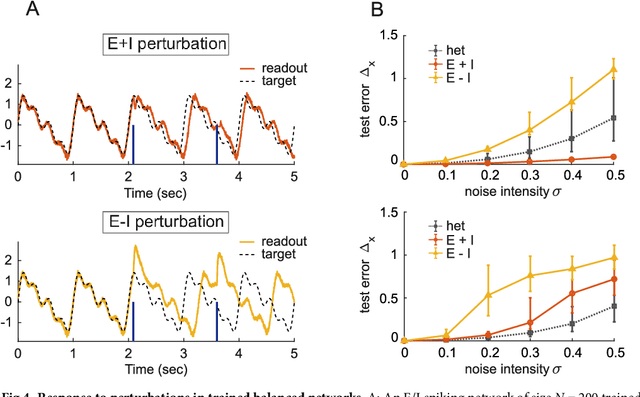
The construction of biologically plausible models of neural circuits is crucial for understanding the computational properties of the nervous system. Constructing functional networks composed of separate excitatory and inhibitory neurons obeying Dale's law presents a number of challenges. We show how a target-based approach, when combined with a fast online constrained optimization technique, is capable of building functional models of rate and spiking recurrent neural networks in which excitation and inhibition are balanced. Balanced networks can be trained to produce complicated temporal patterns and to solve input-output tasks while retaining biologically desirable features such as Dale's law and response variability.

Feedback alignment in deep convolutional networks

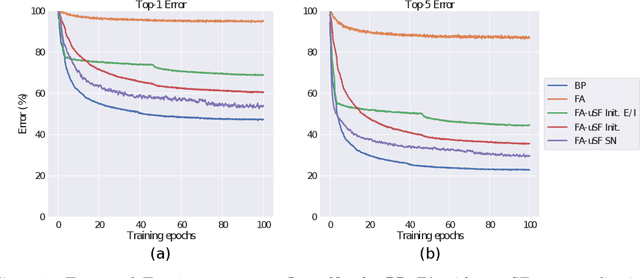
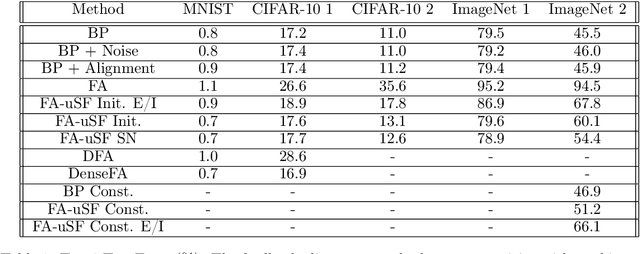
Ongoing studies have identified similarities between neural representations in biological networks and in deep artificial neural networks. This has led to renewed interest in developing analogies between the backpropagation learning algorithm used to train artificial networks and the synaptic plasticity rules operative in the brain. These efforts are challenged by biologically implausible features of backpropagation, one of which is a reliance on symmetric forward and backward synaptic weights. A number of methods have been proposed that do not rely on weight symmetry but, thus far, these have failed to scale to deep convolutional networks and complex data. We identify principal obstacles to the scalability of such algorithms and introduce several techniques to mitigate them. We demonstrate that a modification of the feedback alignment method that enforces a weaker form of weight symmetry, one that requires agreement of weight sign but not magnitude, can achieve performance competitive with backpropagation. Our results complement those of Bartunov et al. (2018) and Xiao et al. (2018b) and suggest that mechanisms that promote alignment of feedforward and feedback weights are critical for learning in deep networks.

full-FORCE: A Target-Based Method for Training Recurrent Networks

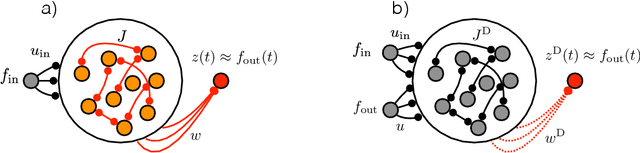
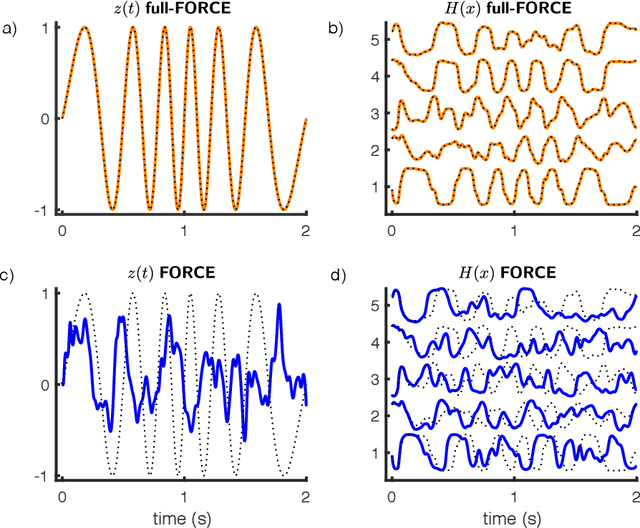
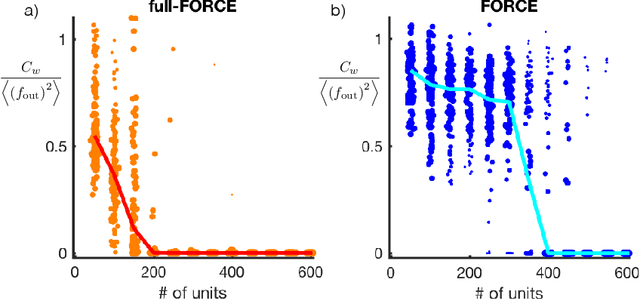
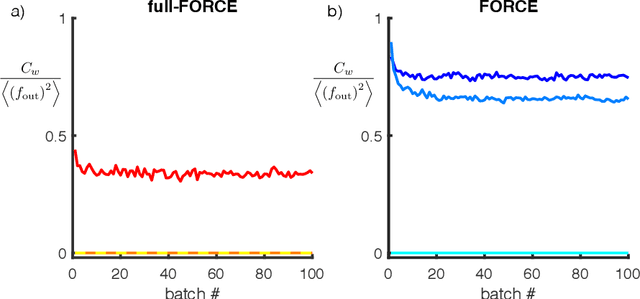
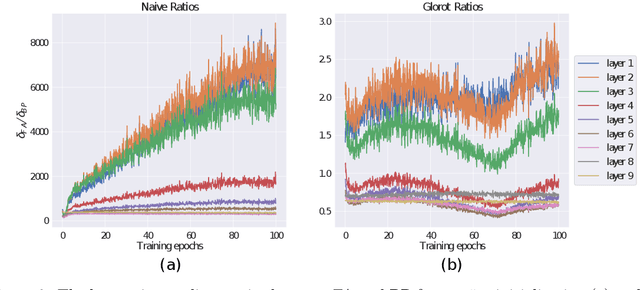
Trained recurrent networks are powerful tools for modeling dynamic neural computations. We present a target-based method for modifying the full connectivity matrix of a recurrent network to train it to perform tasks involving temporally complex input/output transformations. The method introduces a second network during training to provide suitable "target" dynamics useful for performing the task. Because it exploits the full recurrent connectivity, the method produces networks that perform tasks with fewer neurons and greater noise robustness than traditional least-squares (FORCE) approaches. In addition, we show how introducing additional input signals into the target-generating network, which act as task hints, greatly extends the range of tasks that can be learned and provides control over the complexity and nature of the dynamics of the trained, task-performing network.

Balanced Excitation and Inhibition are Required for High-Capacity, Noise-Robust Neuronal Selectivity

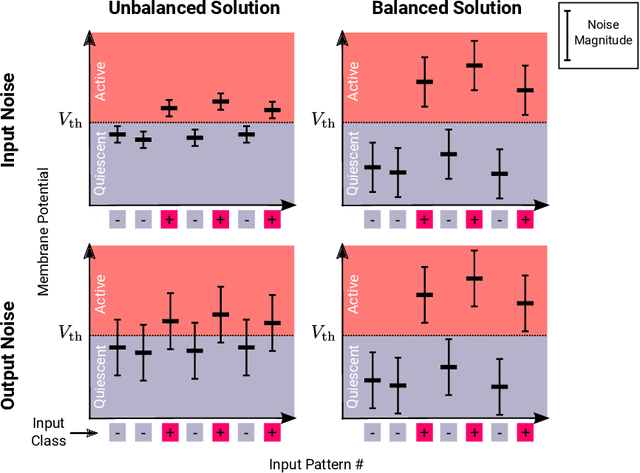
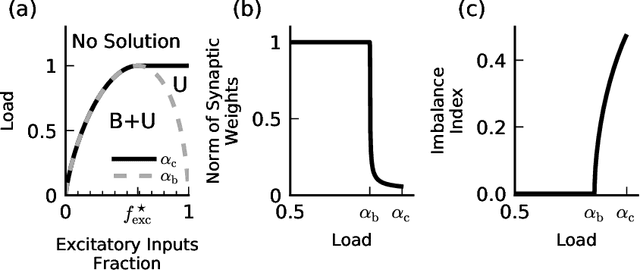
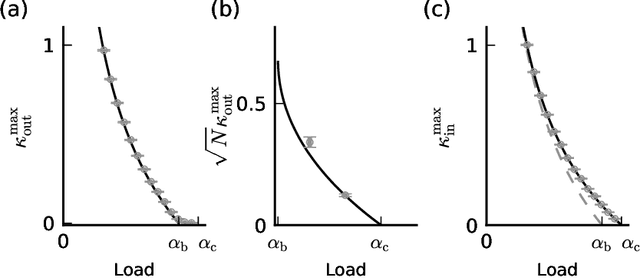
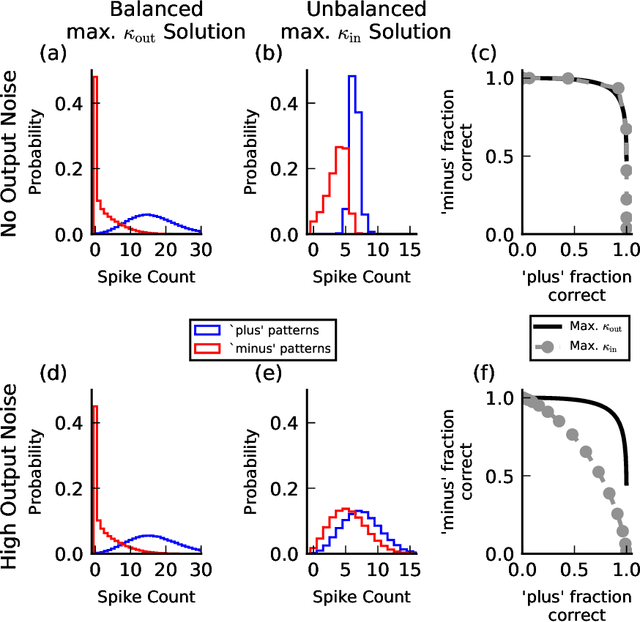
Neurons and networks in the cerebral cortex must operate reliably despite multiple sources of noise. To evaluate the impact of both input and output noise, we determine the robustness of single-neuron stimulus selective responses, as well as the robustness of attractor states of networks of neurons performing memory tasks. We find that robustness to output noise requires synaptic connections to be in a balanced regime in which excitation and inhibition are strong and largely cancel each other. We evaluate the conditions required for this regime to exist and determine the properties of networks operating within it. A plausible synaptic plasticity rule for learning that balances weight configurations is presented. Our theory predicts an optimal ratio of the number of excitatory and inhibitory synapses for maximizing the encoding capacity of balanced networks for a given statistics of afferent activations. Previous work has shown that balanced networks amplify spatio-temporal variability and account for observed asynchronous irregular states. Here we present a novel type of balanced network that amplifies small changes in the impinging signals, and emerges automatically from learning to perform neuronal and network functions robustly.