Local Bayesian Dirichlet mixing of imperfect models

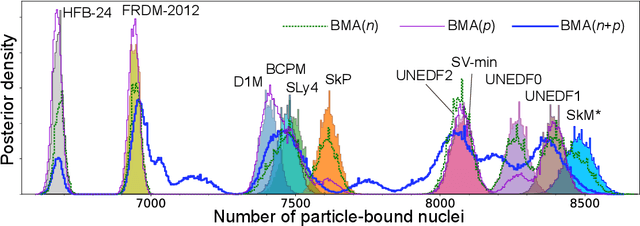
To improve the predictability of complex computational models in the experimentally-unknown domains, we propose a Bayesian statistical machine learning framework utilizing the Dirichlet distribution that combines results of several imperfect models. This framework can be viewed as an extension of Bayesian stacking. To illustrate the method, we study the ability of Bayesian model averaging and mixing techniques to mine nuclear masses. We show that the global and local mixtures of models reach excellent performance on both prediction accuracy and uncertainty quantification and are preferable to classical Bayesian model averaging. Additionally, our statistical analysis indicates that improving model predictions through mixing rather than mixing of corrected models leads to more robust extrapolations.

Statistical aspects of nuclear mass models

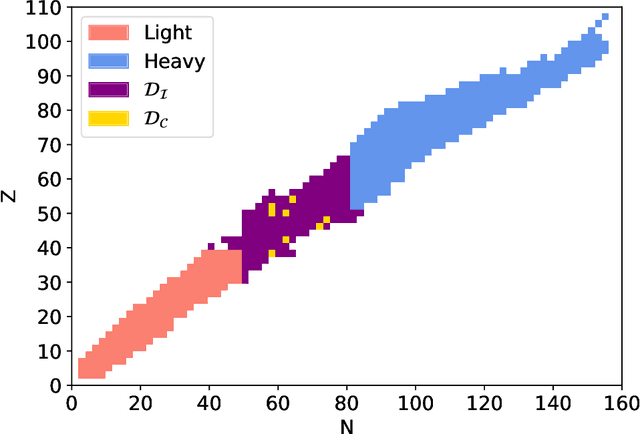
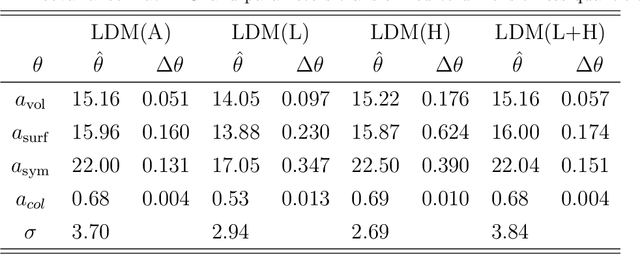
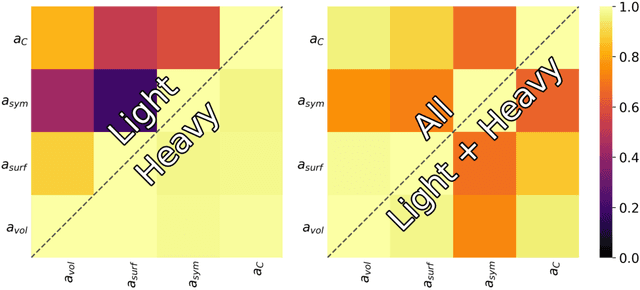
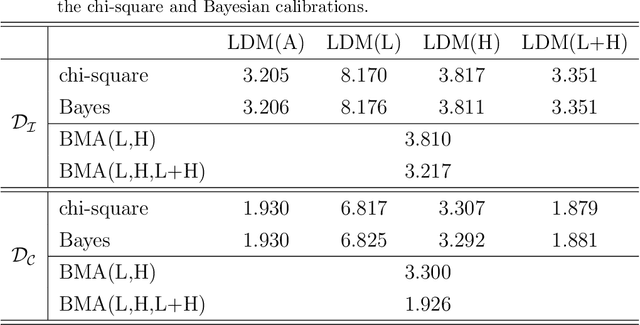
We study the information content of nuclear masses from the perspective of global models of nuclear binding energies. To this end, we employ a number of statistical methods and diagnostic tools, including Bayesian calibration, Bayesian model averaging, chi-square correlation analysis, principal component analysis, and empirical coverage probability. Using Bayesian framework, we investigate the structure of the 4-parameter Liquid Drop Model by considering discrepant mass domains for calibration. We then use the chi-square correlation framework to analyze the 14-parameter Skyrme energy density functional calibrated using homogeneous and heterogeneous datasets. We show that a quite dramatic parameter reduction can be achieved in both cases. The advantage of the Bayesian model averaging for improving the uncertainty quantification is demonstrated. The statistical approaches used are pedagogically described; in this context this work can serve as a guide for future applications.

Quantified limits of the nuclear landscape

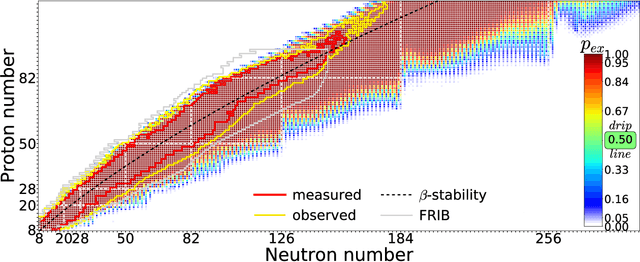
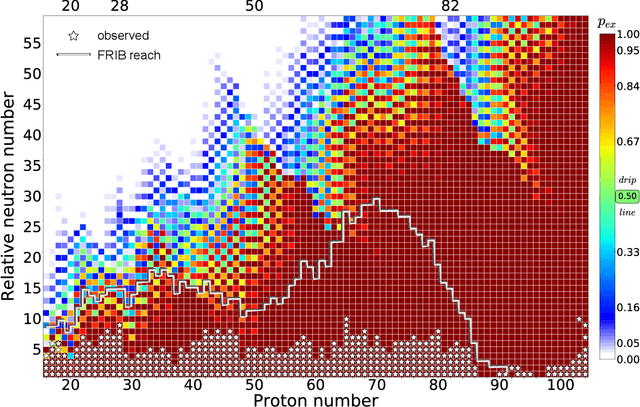
The chart of the nuclides is limited by particle drip lines beyond which nuclear stability to proton or neutron emission is lost. Predicting the range of particle-bound isotopes poses an appreciable challenge for nuclear theory as it involves extreme extrapolations of nuclear masses beyond the regions where experimental information is available. Still, quantified extrapolations are crucial for a variety of applications, including the modeling of stellar nucleosynthesis. We use microscopic nuclear mass models and Bayesian methodology to provide quantified predictions of proton and neutron separation energies as well as Bayesian probabilities of existence throughout the nuclear landscape all the way to the particle drip lines. We apply nuclear density functional theory with several energy density functionals. To account for uncertainties, Bayesian Gaussian processes are trained on the separation-energy residuals for each individual model, and the resulting predictions are combined via Bayesian model averaging. This framework allows to account for systematic and statistical uncertainties and propagate them to extrapolative predictions. We characterize the drip-line regions where the probability that the nucleus is particle-bound decreases from $1$ to $0$. In these regions, we provide quantified predictions for one- and two-nucleon separation energies. According to our Bayesian model averaging analysis, 7759 nuclei with $Z\leq 119$ have a probability of existence $\geq 0.5$. The extrapolations obtained in this study will be put through stringent tests when new experimental information on exotic nuclei becomes available. In this respect, the quantified landscape of nuclear existence obtained in this study should be viewed as a dynamical prediction that will be fine-tuned when new experimental information and improved global mass models become available.

Beyond the proton drip line: Bayesian analysis of proton-emitting nuclei

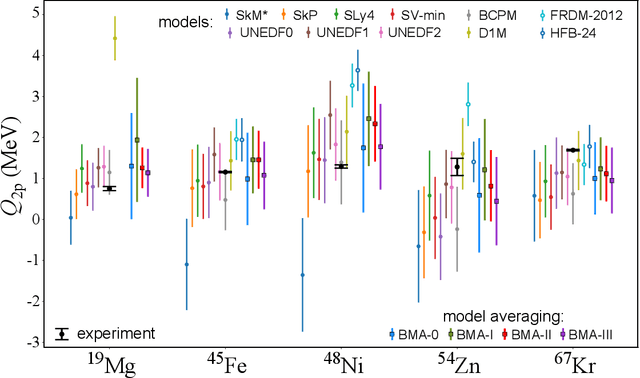
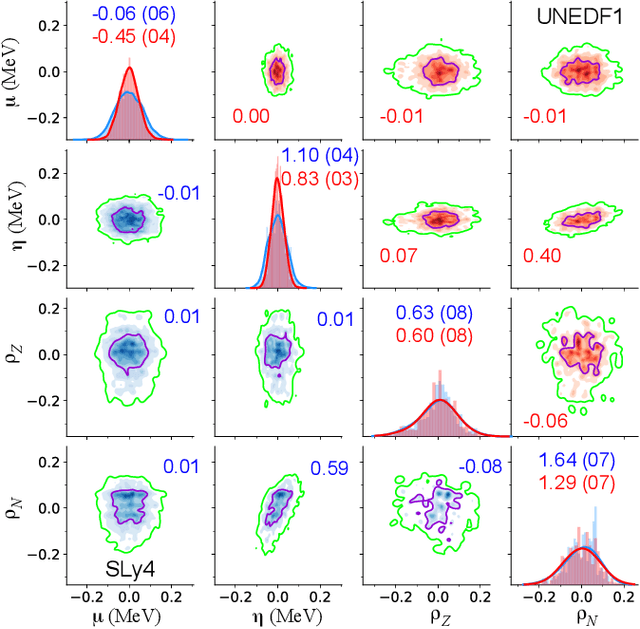
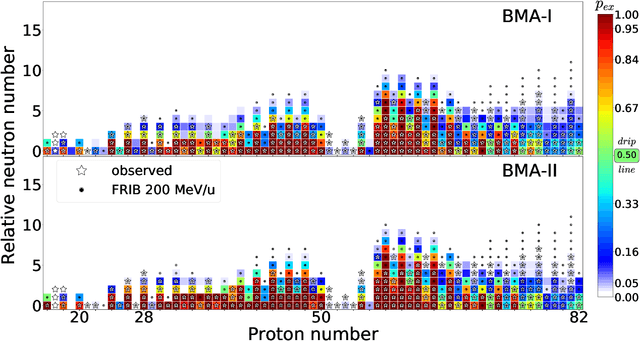
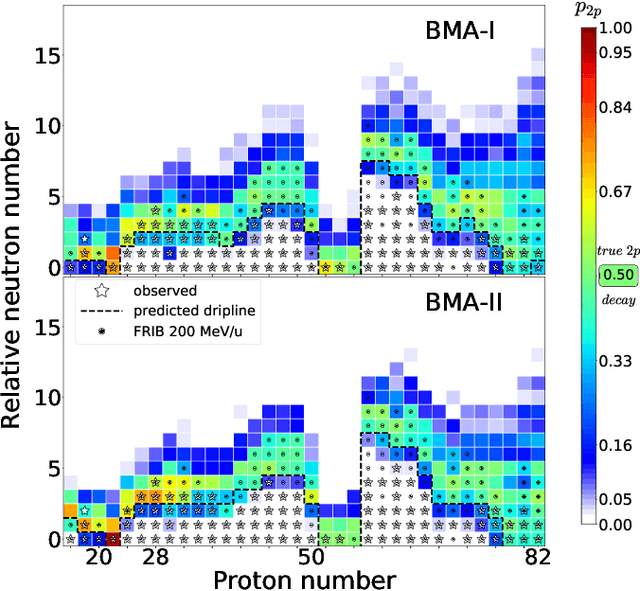
The limits of the nuclear landscape are determined by nuclear binding energies. Beyond the proton drip lines, where the separation energy becomes negative, there is not enough binding energy to prevent protons from escaping the nucleus. Predicting properties of unstable nuclear states in the vast territory of proton emitters poses an appreciable challenge for nuclear theory as it often involves far extrapolations. In addition, significant discrepancies between nuclear models in the proton-rich territory call for quantified predictions. With the help of Bayesian methodology, we mix a family of nuclear mass models corrected with statistical emulators trained on the experimental mass measurements, in the proton-rich region of the nuclear chart. Separation energies were computed within nuclear density functional theory using several Skyrme and Gogny energy density functionals. We also considered mass predictions based on two models used in astrophysical studies. Quantified predictions were obtained for each model using Bayesian Gaussian processes trained on separation-energy residuals and combined via Bayesian model averaging. We obtained a good agreement between averaged predictions of statistically corrected models and experiment. In particular, we quantified model results for one- and two-proton separation energies and derived probabilities of proton emission. This information enabled us to produce a quantified landscape of proton-rich nuclei. The most promising candidates for two-proton decay studies have been identified. The methodology used in this work has broad applications to model-based extrapolations of various nuclear observables. It also provides a reliable uncertainty quantification of theoretical predictions.

Neutron drip line in the Ca region from Bayesian model averaging

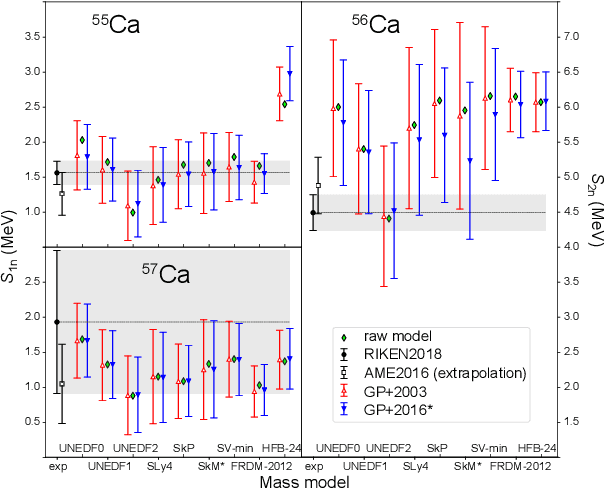
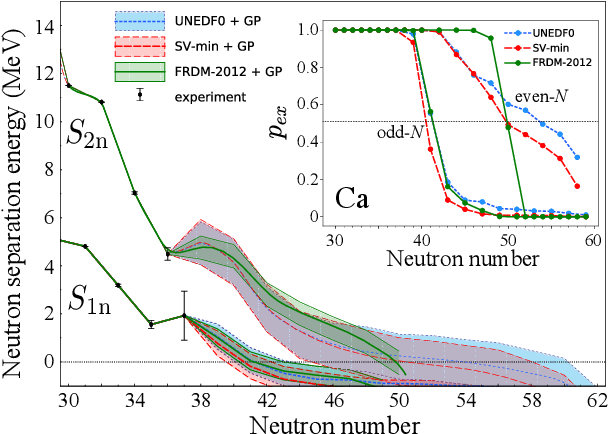
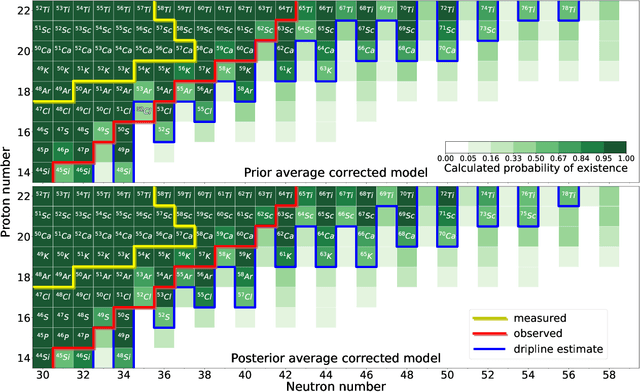
The region of heavy calcium isotopes forms the frontier of experimental and theoretical nuclear structure research where the basic concepts of nuclear physics are put to stringent test. The recent discovery of the extremely neutron-rich nuclei around $^{60}$Ca [Tarasov, 2018] and the experimental determination of masses for $^{55-57}$Ca (Michimasa, 2018] provide unique information about the binding energy surface in this region. To assess the impact of these experimental discoveries on the nuclear landscape's extent, we use global mass models and statistical machine learning to make predictions, with quantified levels of certainty, for bound nuclides between Si and Ti. Using a Bayesian model averaging analysis based on Gaussian-process-based extrapolations we introduce the posterior probability $p_{ex}$ for each nucleus to be bound to neutron emission. We find that extrapolations for drip-line locations, at which the nuclear binding ends, are consistent across the global mass models used, in spite of significant variations between their raw predictions. In particular, considering the current experimental information and current global mass models, we predict that $^{68}$Ca has an average posterior probability ${p_{ex}\approx76}$% to be bound to two-neutron emission while the nucleus $^{61}$Ca is likely to decay by emitting a neutron (${p_{ex}\approx 46}$ %).

Bayesian approach to model-based extrapolation of nuclear observables

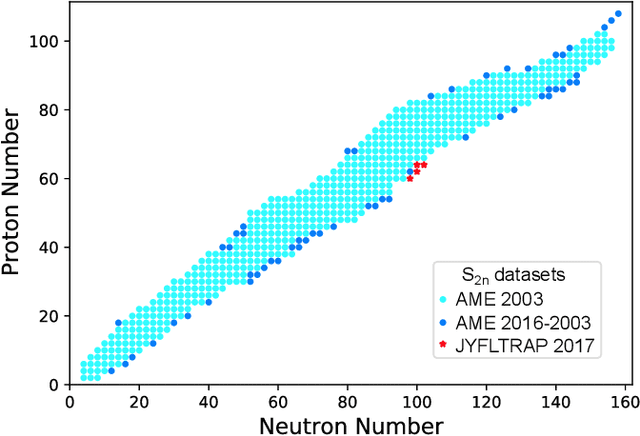
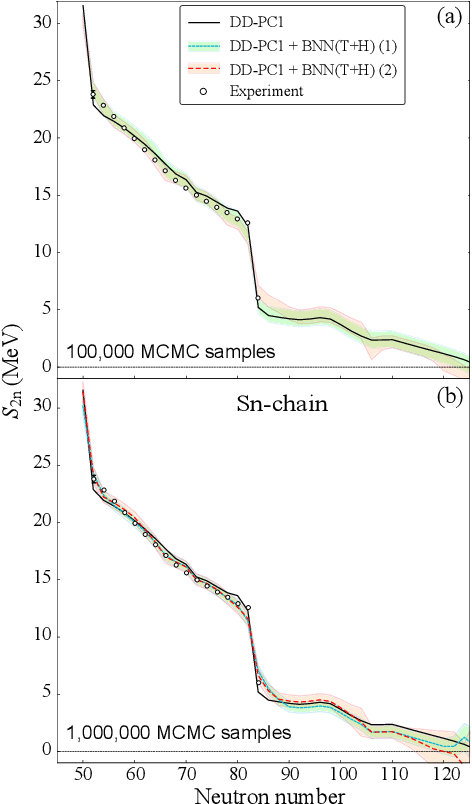
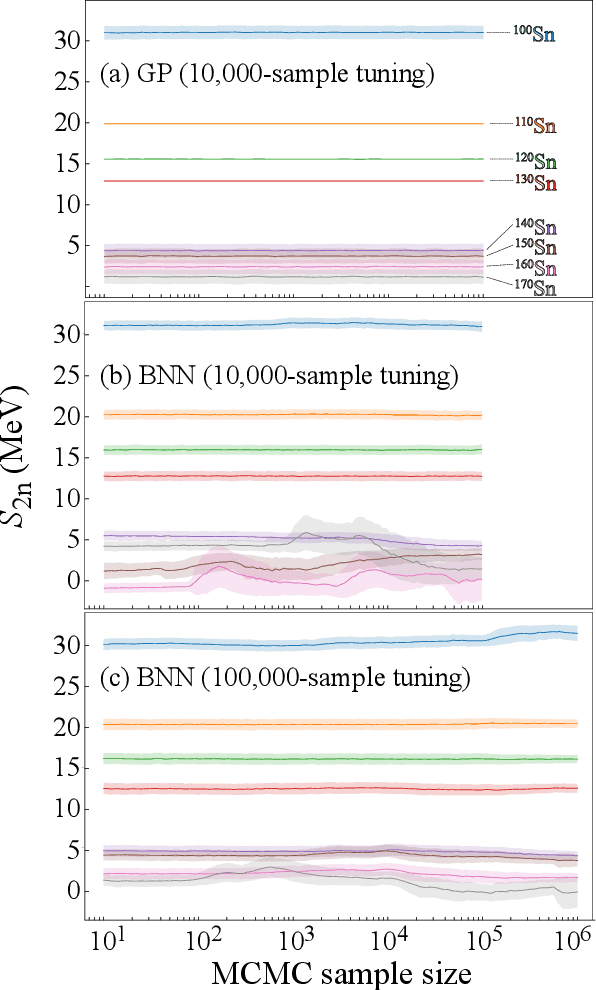
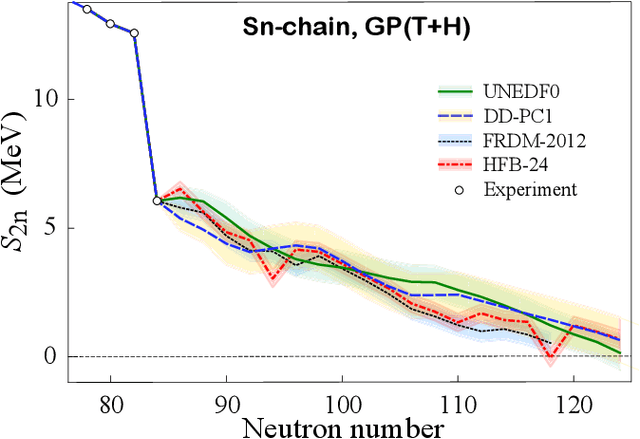
The mass, or binding energy, is the basis property of the atomic nucleus. It determines its stability, and reaction and decay rates. Quantifying the nuclear binding is important for understanding the origin of elements in the universe. The astrophysical processes responsible for the nucleosynthesis in stars often take place far from the valley of stability, where experimental masses are not known. In such cases, missing nuclear information must be provided by theoretical predictions using extreme extrapolations. Bayesian machine learning techniques can be applied to improve predictions by taking full advantage of the information contained in the deviations between experimental and calculated masses. We consider 10 global models based on nuclear Density Functional Theory as well as two more phenomenological mass models. The emulators of S2n residuals and credibility intervals defining theoretical error bars are constructed using Bayesian Gaussian processes and Bayesian neural networks. We consider a large training dataset pertaining to nuclei whose masses were measured before 2003. For the testing datasets, we considered those exotic nuclei whose masses have been determined after 2003. We then carried out extrapolations towards the 2n dripline. While both Gaussian processes and Bayesian neural networks reduce the rms deviation from experiment significantly, GP offers a better and much more stable performance. The increase in the predictive power is quite astonishing: the resulting rms deviations from experiment on the testing dataset are similar to those of more phenomenological models. The empirical coverage probability curves we obtain match very well the reference values which is highly desirable to ensure honesty of uncertainty quantification, and the estimated credibility intervals on predictions make it possible to evaluate predictive power of individual models.