General Post-Processing Framework for Fairness Adjustment of Machine Learning Models

As machine learning increasingly influences critical domains such as credit underwriting, public policy, and talent acquisition, ensuring compliance with fairness constraints is both a legal and ethical imperative. This paper introduces a novel framework for fairness adjustments that applies to diverse machine learning tasks, including regression and classification, and accommodates a wide range of fairness metrics. Unlike traditional approaches categorized as pre-processing, in-processing, or post-processing, our method adapts in-processing techniques for use as a post-processing step. By decoupling fairness adjustments from the model training process, our framework preserves model performance on average while enabling greater flexibility in model development. Key advantages include eliminating the need for custom loss functions, enabling fairness tuning using different datasets, accommodating proprietary models as black-box systems, and providing interpretable insights into the fairness adjustments. We demonstrate the effectiveness of this approach by comparing it to Adversarial Debiasing, showing that our framework achieves a comparable fairness/accuracy tradeoff on real-world datasets.

High-Dimensional Distribution Generation Through Deep Neural Networks

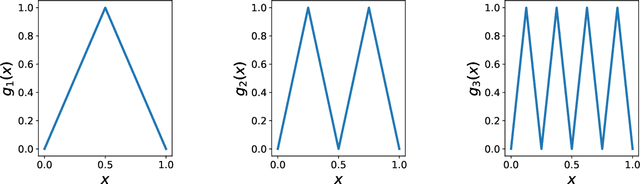
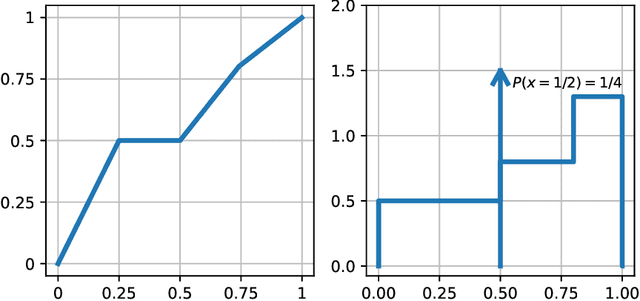
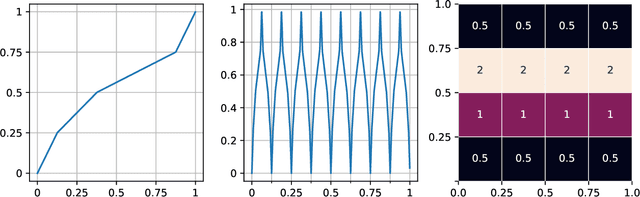
We show that every $d$-dimensional probability distribution of bounded support can be generated through deep ReLU networks out of a $1$-dimensional uniform input distribution. What is more, this is possible without incurring a cost - in terms of approximation error measured in Wasserstein-distance - relative to generating the $d$-dimensional target distribution from $d$ independent random variables. This is enabled by a vast generalization of the space-filling approach discovered in (Bailey & Telgarsky, 2018). The construction we propose elicits the importance of network depth in driving the Wasserstein distance between the target distribution and its neural network approximation to zero. Finally, we find that, for histogram target distributions, the number of bits needed to encode the corresponding generative network equals the fundamental limit for encoding probability distributions as dictated by quantization theory.