Kurt Mehlhorn
Physarum Multi-Commodity Flow Dynamics
Sep 23, 2020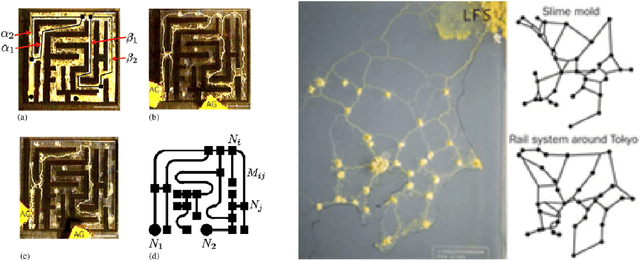
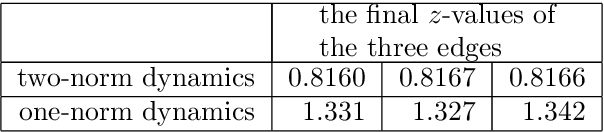
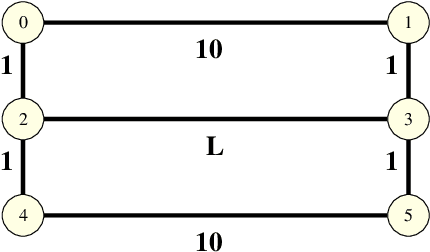
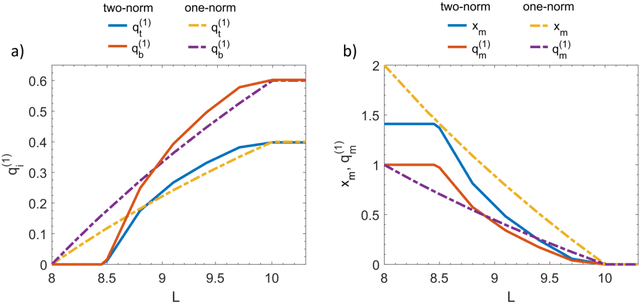
Abstract:In wet-lab experiments \cite{Nakagaki-Yamada-Toth,Tero-Takagi-etal}, the slime mold Physarum polycephalum has demonstrated its ability to solve shortest path problems and to design efficient networks, see Figure \ref{Wet-Lab Experiments} for illustrations. Physarum polycephalum is a slime mold in the Mycetozoa group. For the shortest path problem, a mathematical model for the evolution of the slime was proposed in \cite{Tero-Kobayashi-Nakagaki} and its biological relevance was argued. The model was shown to solve shortest path problems, first in computer simulations and then by mathematical proof. It was later shown that the slime mold dynamics can solve more general linear programs and that many variants of the dynamics have similar convergence behavior. In this paper, we introduce a dynamics for the network design problem. We formulate network design as the problem of constructing a network that efficiently supports a multi-commodity flow problem. We investigate the dynamics in computer simulations and analytically. The simulations show that the dynamics is able to construct efficient and elegant networks. In the theoretical part we show that the dynamics minimizes an objective combining the cost of the network and the cost of routing the demands through the network. We also give alternative characterization of the optimum solution.
The Query Complexity of a Permutation-Based Variant of Mastermind
Dec 20, 2018Abstract:We study the query complexity of a permutation-based variant of the guessing game Mastermind. In this variant, the secret is a pair $(z,\pi)$ which consists of a binary string $z \in \{0,1\}^n$ and a permutation $\pi$ of $[n]$. The secret must be unveiled by asking queries of the form $x \in \{0,1\}^n$. For each such query, we are returned the score \[ f_{z,\pi}(x):= \max \{ i \in [0..n]\mid \forall j \leq i: z_{\pi(j)} = x_{\pi(j)}\}\,;\] i.e., the score of $x$ is the length of the longest common prefix of $x$ and $z$ with respect to the order imposed by $\pi$. The goal is to minimize the number of queries needed to identify $(z,\pi)$. This problem originates from the study of black-box optimization heuristics, where it is known as the \textsc{LeadingOnes} problem. In this work, we prove matching upper and lower bounds for the deterministic and randomized query complexity of this game, which are $\Theta(n \log n)$ and $\Theta(n \log \log n)$, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge