Boundary condition enforcement with PINNs: a comparative study and verification on 3D geometries

Since their advent nearly a decade ago, physics-informed neural networks (PINNs) have been studied extensively as a novel technique for solving forward and inverse problems in physics and engineering. The neural network discretization of the solution field is naturally adaptive and avoids meshing the computational domain, which can both improve the accuracy of the numerical solution and streamline implementation. However, there have been limited studies of PINNs on complex three-dimensional geometries, as the lack of mesh and the reliance on the strong form of the partial differential equation (PDE) make boundary condition (BC) enforcement challenging. Techniques to enforce BCs with PINNs have proliferated in the literature, but a comprehensive side-by-side comparison of these techniques and a study of their efficacy on geometrically complex three-dimensional test problems are lacking. In this work, we i) systematically compare BC enforcement techniques for PINNs, ii) propose a general solution framework for arbitrary three-dimensional geometries, and iii) verify the methodology on three-dimensional, linear and nonlinear test problems with combinations of Dirichlet, Neumann, and Robin boundaries. Our approach is agnostic to the underlying PDE, the geometry of the computational domain, and the nature of the BCs, while requiring minimal hyperparameter tuning. This work represents a step in the direction of establishing PINNs as a mature numerical method, capable of competing head-to-head with incumbents such as the finite element method.

Solving engineering eigenvalue problems with neural networks using the Rayleigh quotient

From characterizing the speed of a thermal system's response to computing natural modes of vibration, eigenvalue analysis is ubiquitous in engineering. In spite of this, eigenvalue problems have received relatively little treatment compared to standard forward and inverse problems in the physics-informed machine learning literature. In particular, neural network discretizations of solutions to eigenvalue problems have seen only a handful of studies. Owing to their nonlinearity, neural network discretizations prevent the conversion of the continuous eigenvalue differential equation into a standard discrete eigenvalue problem. In this setting, eigenvalue analysis requires more specialized techniques. Using a neural network discretization of the eigenfunction, we show that a variational form of the eigenvalue problem called the "Rayleigh quotient" in tandem with a Gram-Schmidt orthogonalization procedure is a particularly simple and robust approach to find the eigenvalues and their corresponding eigenfunctions. This method is shown to be useful for finding sets of harmonic functions on irregular domains, parametric and nonlinear eigenproblems, and high-dimensional eigenanalysis. We also discuss the utility of harmonic functions as a spectral basis for approximating solutions to partial differential equations. Through various examples from engineering mechanics, the combination of the Rayleigh quotient objective, Gram-Schmidt procedure, and the neural network discretization of the eigenfunction is shown to offer unique advantages for handling continuous eigenvalue problems.

Physics-informed solution reconstruction in elasticity and heat transfer using the explicit constraint force method

One use case of ``physics-informed neural networks'' (PINNs) is solution reconstruction, which aims to estimate the full-field state of a physical system from sparse measurements. Parameterized governing equations of the system are used in tandem with the measurements to regularize the regression problem. However, in real-world solution reconstruction problems, the parameterized governing equation may be inconsistent with the physical phenomena that give rise to the measurement data. We show that due to assuming consistency between the true and parameterized physics, PINNs-based approaches may fail to satisfy three basic criteria of interpretability, robustness, and data consistency. As we argue, these criteria ensure that (i) the quality of the reconstruction can be assessed, (ii) the reconstruction does not depend strongly on the choice of physics loss, and (iii) that in certain situations, the physics parameters can be uniquely recovered. In the context of elasticity and heat transfer, we demonstrate how standard formulations of the physics loss and techniques for constraining the solution to respect the measurement data lead to different ``constraint forces" -- which we define as additional source terms arising from the constraints -- and that these constraint forces can significantly influence the reconstructed solution. To avoid the potentially substantial influence of the choice of physics loss and method of constraint enforcement on the reconstructed solution, we propose the ``explicit constraint force method'' (ECFM) to gain control of the source term introduced by the constraint. We then show that by satisfying the criteria of interpretability, robustness, and data consistency, this approach leads to more predictable and customizable reconstructions from noisy measurement data, even when the parameterization of the missing physics is inconsistent with the measured system.

Constrained or Unconstrained? Neural-Network-Based Equation Discovery from Data

Throughout many fields, practitioners often rely on differential equations to model systems. Yet, for many applications, the theoretical derivation of such equations and/or accurate resolution of their solutions may be intractable. Instead, recently developed methods, including those based on parameter estimation, operator subset selection, and neural networks, allow for the data-driven discovery of both ordinary and partial differential equations (PDEs), on a spectrum of interpretability. The success of these strategies is often contingent upon the correct identification of representative equations from noisy observations of state variables and, as importantly and intertwined with that, the mathematical strategies utilized to enforce those equations. Specifically, the latter has been commonly addressed via unconstrained optimization strategies. Representing the PDE as a neural network, we propose to discover the PDE by solving a constrained optimization problem and using an intermediate state representation similar to a Physics-Informed Neural Network (PINN). The objective function of this constrained optimization problem promotes matching the data, while the constraints require that the PDE is satisfied at several spatial collocation points. We present a penalty method and a widely used trust-region barrier method to solve this constrained optimization problem, and we compare these methods on numerical examples. Our results on the Burgers' and the Korteweg-De Vreis equations demonstrate that the latter constrained method outperforms the penalty method, particularly for higher noise levels or fewer collocation points. For both methods, we solve these discovered neural network PDEs with classical methods, such as finite difference methods, as opposed to PINNs-type methods relying on automatic differentiation. We briefly highlight other small, yet crucial, implementation details.

Automated processing of X-ray computed tomography images via panoptic segmentation for modeling woven composite textiles

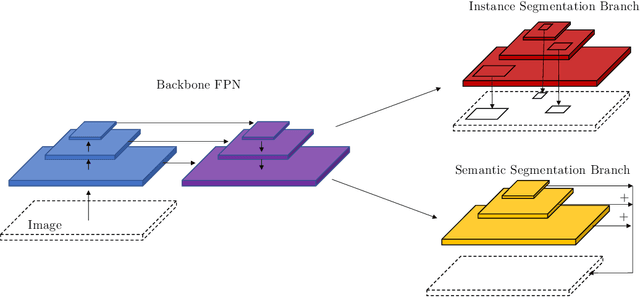
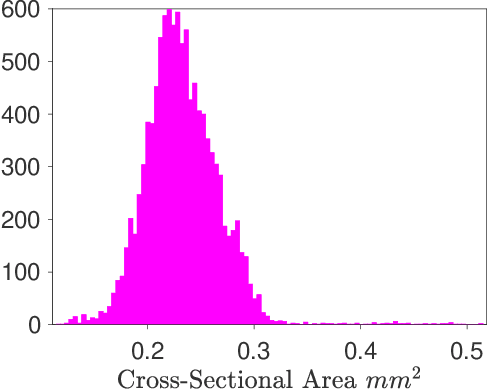
A new, machine learning-based approach for automatically generating 3D digital geometries of woven composite textiles is proposed to overcome the limitations of existing analytical descriptions and segmentation methods. In this approach, panoptic segmentation is leveraged to produce instance segmented semantic masks from X-ray computed tomography (CT) images. This effort represents the first deep learning based automated process for segmenting unique yarn instances in a woven composite textile. Furthermore, it improves on existing methods by providing instance-level segmentation on low contrast CT datasets. Frame-to-frame instance tracking is accomplished via an intersection-over-union (IoU) approach adopted from video panoptic segmentation for assembling a 3D geometric model. A corrective recognition algorithm is developed to improve the recognition quality (RQ). The panoptic quality (PQ) metric is adopted to provide a new universal evaluation metric for reconstructed woven composite textiles. It is found that the panoptic segmentation network generalizes well to new CT images that are similar to the training set but does not extrapolate well to CT images of differing geometry, texture, and contrast. The utility of this approach is demonstrated by capturing yarn flow directions, contact regions between individual yarns, and the spatially varying cross-sectional areas of the yarns.