AdaSD: Adaptive Speculative Decoding for Efficient Language Model Inference

Large language models (LLMs) have achieved remarkable performance across a wide range of tasks, but their increasing parameter sizes significantly slow down inference. Speculative decoding mitigates this issue by leveraging a smaller draft model to predict candidate tokens, which are then verified by a larger target model. However, existing approaches often require additional training, extensive hyperparameter tuning, or prior analysis of models and tasks before deployment. In this paper, we propose Adaptive Speculative Decoding (AdaSD), a hyperparameter-free decoding scheme that dynamically adjusts generation length and acceptance criteria during inference. AdaSD introduces two adaptive thresholds: one to determine when to stop candidate token generation and another to decide token acceptance, both updated in real time based on token entropy and Jensen-Shannon distance. This approach eliminates the need for pre-analysis or fine-tuning and is compatible with off-the-shelf models. Experiments on benchmark datasets demonstrate that AdaSD achieves up to 49\% speedup over standard speculative decoding while limiting accuracy degradation to under 2\%, making it a practical solution for efficient and adaptive LLM inference.

Robust 360-8PA: Redesigning The Normalized 8-point Algorithm for 360-FoV Images

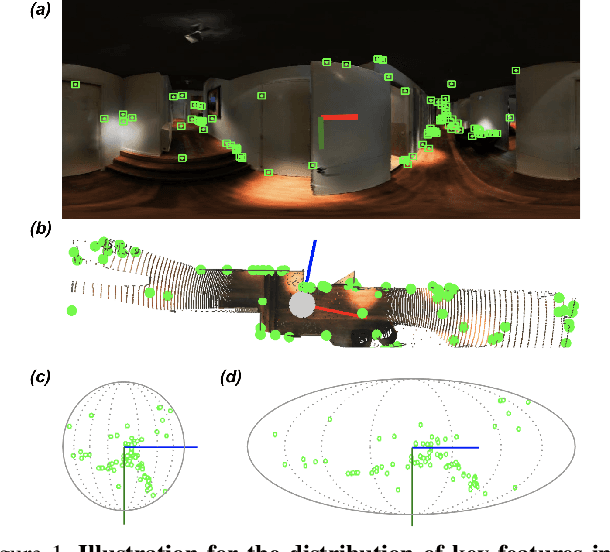
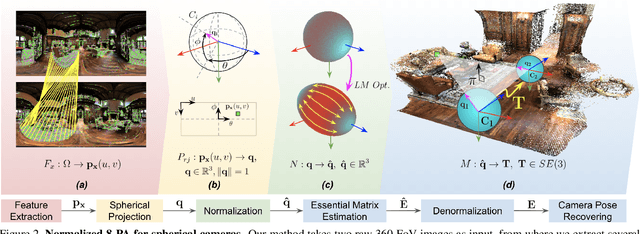
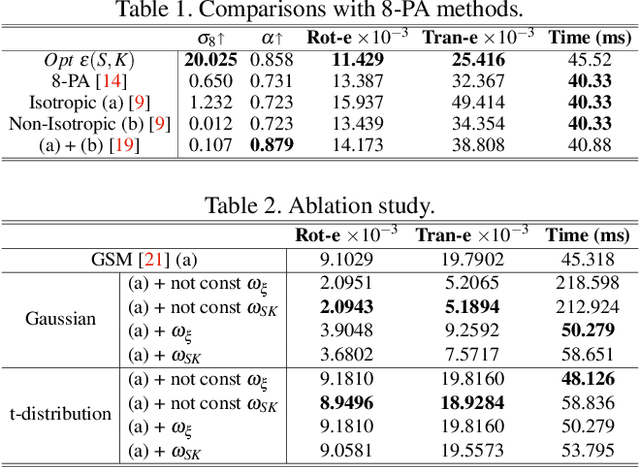
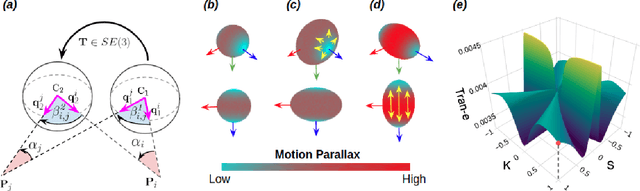
This paper presents a novel preconditioning strategy for the classic 8-point algorithm (8-PA) for estimating an essential matrix from 360-FoV images (i.e., equirectangular images) in spherical projection. To alleviate the effect of uneven key-feature distributions and outlier correspondences, which can potentially decrease the accuracy of an essential matrix, our method optimizes a non-rigid transformation to deform a spherical camera into a new spatial domain, defining a new constraint and a more robust and accurate solution for an essential matrix. Through several experiments using random synthetic points, 360-FoV, and fish-eye images, we demonstrate that our normalization can increase the camera pose accuracy by about 20% without significantly overhead the computation time. In addition, we present further benefits of our method through both a constant weighted least-square optimization that improves further the well known Gold Standard Method (GSM) (i.e., the non-linear optimization by using epipolar errors); and a relaxation of the number of RANSAC iterations, both showing that our normalization outcomes a more reliable, robust, and accurate solution.