Model parameter estimation using coherent structure coloring

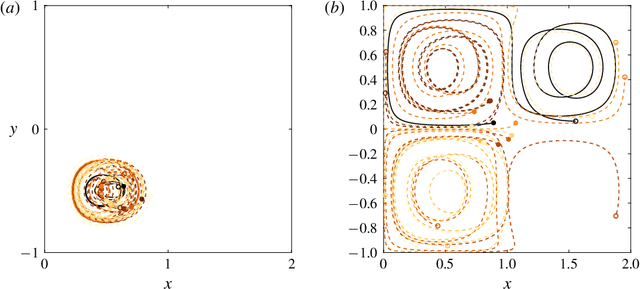
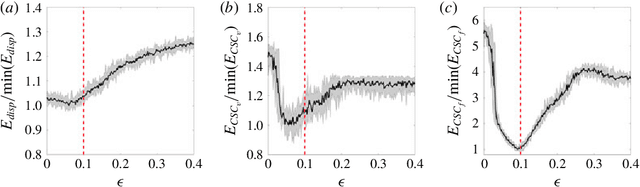
Lagrangian data assimilation is a complex problem in oceanic and atmospheric modeling. Tracking drifters in large-scale geophysical flows can involve uncertainty in drifter location, complex inertial effects, and other factors which make comparing them to simulated Lagrangian trajectories from numerical models extremely challenging. Temporal and spatial discretization, factors necessary in modeling large scale flows, also contribute to separation between real and simulated drifter trajectories. The chaotic advection inherent in these turbulent flows tends to separate even closely spaced tracer particles, making error metrics based solely on drifter displacements unsuitable for estimating model parameters. We propose to instead use error in the coherent structure coloring (CSC) field to assess model skill. The CSC field provides a spatial representation of the underlying coherent patterns in the flow, and we show that it is a more robust metric for assessing model accuracy. Through the use of two test cases, one considering spatial uncertainty in particle initialization, and one examining the influence of stochastic error along a trajectory and temporal discretization, we show that error in the coherent structure coloring field can be used to accurately determine single or multiple simultaneously unknown model parameters, whereas a conventional error metric based on error in drifter displacement fails. Because the CSC field enhances the difference in error between correct and incorrect model parameters, error minima in model parameter sweeps become more distinct. The effectiveness and robustness of this method for single and multi-parameter estimation in analytical flows suggests that Lagrangian data assimilation for real oceanic and atmospheric models would benefit from a similar approach.

Simultaneous Coherent Structure Coloring facilitates interpretable clustering of scientific data by amplifying dissimilarity

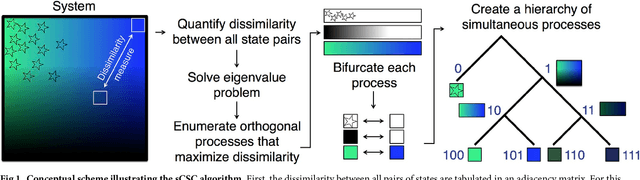
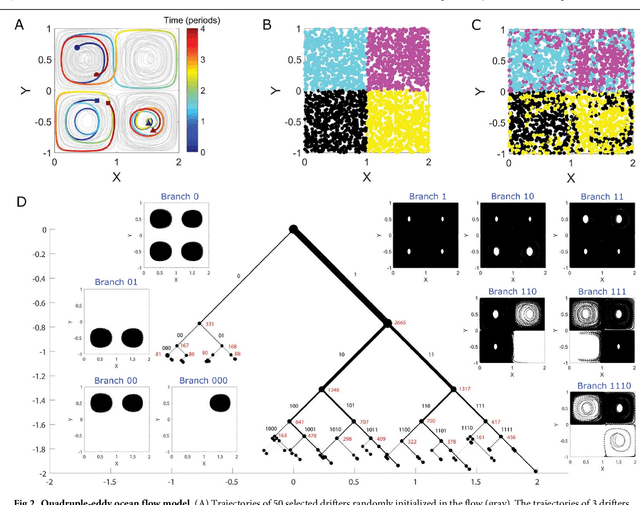
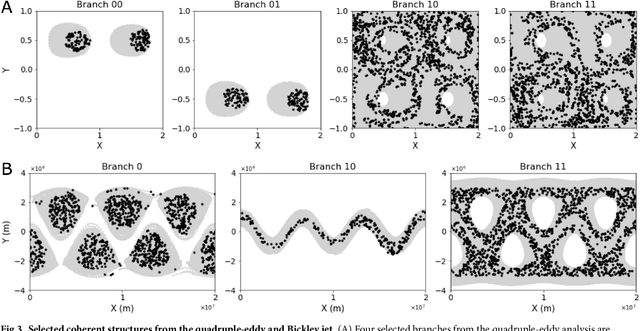
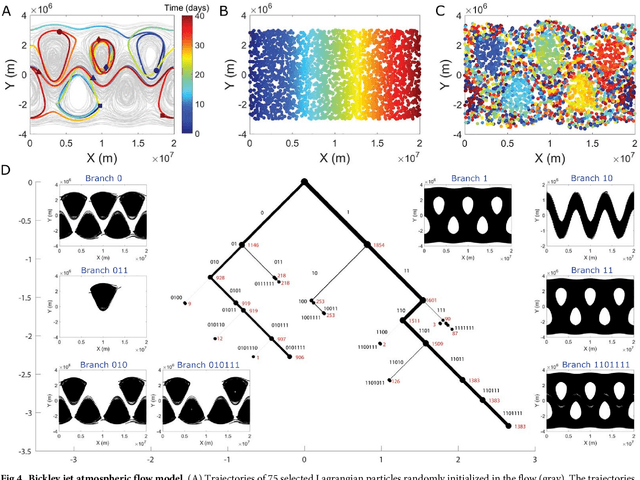
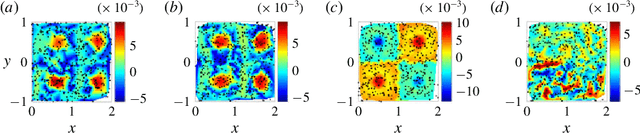
The clustering of data into physically meaningful subsets often requires assumptions regarding the number, size, or shape of the subgroups. Here, we present a new method, simultaneous Coherent Structure Coloring (sCSC), which accomplishes the task of unsupervised clustering without a priori guidance regarding the underlying structure of the data. sCSC performs a sequence of binary splittings on the dataset such that the most dissimilar data points are required to be in separate clusters. To achieve this, we obtain a set of orthogonal coordinates along which dissimilarity in the dataset is maximized from a generalized eigenvalue problem based on the pairwise dissimilarity between the data points to be clustered. This sequence of bifurcations produces a binary tree representation of the system, from which the number of clusters in the data and their interrelationships naturally emerge. To illustrate the effectiveness of the method in the absence of a priori assumptions we apply it to two exemplary problems in fluid dynamics. Then, we illustrate its capacity for interpretability using a high-dimensional protein folding simulation dataset. While we restrict our examples to dynamical physical systems in this work, we anticipate straightforward translation to other fields where existing analysis tools require ad hoc assumptions on the data structure, lack the interpretability of the present method, or in which the underlying processes are less accessible, such as genomics and neuroscience.

Identification of individual coherent sets associated with flow trajectories using Coherent Structure Coloring

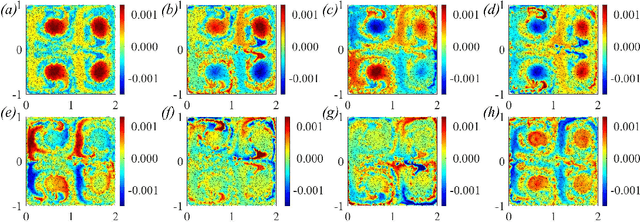
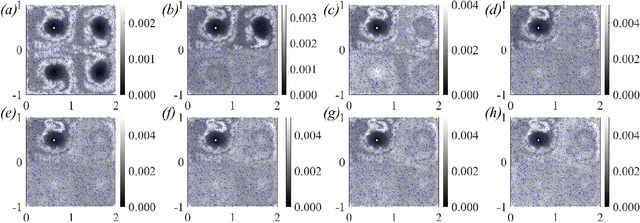
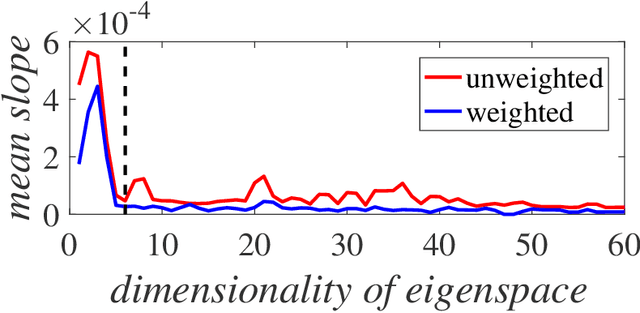
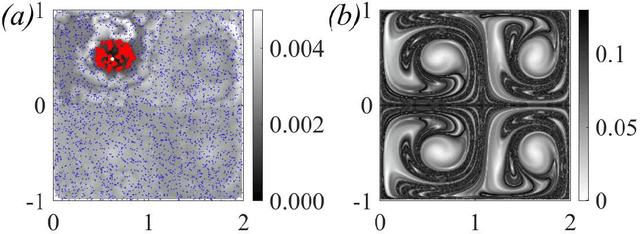
We present a method for identifying the coherent structures associated with individual Lagrangian flow trajectories even where only sparse particle trajectory data is available. The method, based on techniques in spectral graph theory, uses the Coherent Structure Coloring vector and associated eigenvectors to analyze the distance in higher-dimensional eigenspace between a selected reference trajectory and other tracer trajectories in the flow. By analyzing this distance metric in a hierarchical clustering, the coherent structure of which the reference particle is a member can be identified. This algorithm is proven successful in identifying coherent structures of varying complexities in canonical unsteady flows. Additionally, the method is able to assess the relative coherence of the associated structure in comparison to the surrounding flow. Although the method is demonstrated here in the context of fluid flow kinematics, the generality of the approach allows for its potential application to other unsupervised clustering problems in dynamical systems such as neuronal activity, gene expression, or social networks.

Coherent structure coloring: identification of coherent structures from sparse data using graph theory

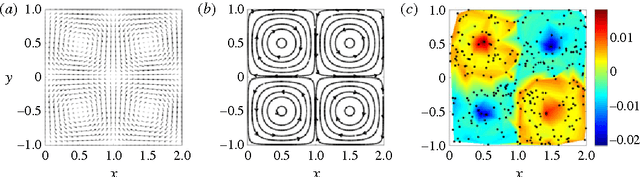
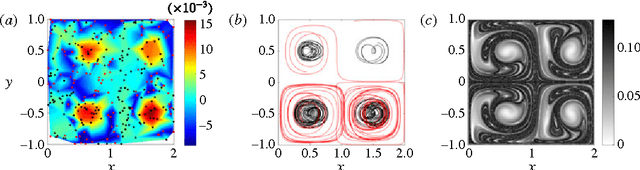
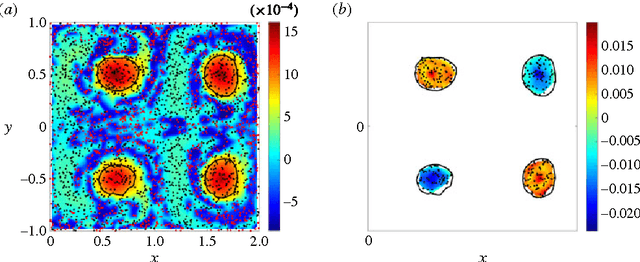
We present a frame-invariant method for detecting coherent structures from Lagrangian flow trajectories that can be sparse in number, as is the case in many fluid mechanics applications of practical interest. The method, based on principles used in graph coloring and spectral graph drawing algorithms, examines a measure of the kinematic dissimilarity of all pairs of fluid trajectories, either measured experimentally, e.g. using particle tracking velocimetry; or numerically, by advecting fluid particles in the Eulerian velocity field. Coherence is assigned to groups of particles whose kinematics remain similar throughout the time interval for which trajectory data is available, regardless of their physical proximity to one another. Through the use of several analytical and experimental validation cases, this algorithm is shown to robustly detect coherent structures using significantly less flow data than is required by existing spectral graph theory methods.