Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Learning to Persuade on the Fly: Robustness Against Ignorance

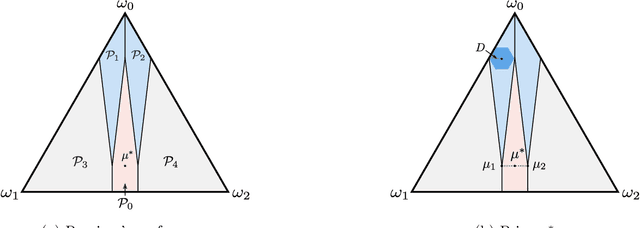
We study a repeated persuasion setting between a sender and a receiver, where at each time $t$, the sender observes a payoff-relevant state drawn independently and identically from an unknown prior distribution, and shares state information with the receiver, who then myopically chooses an action. As in the standard setting, the sender seeks to persuade the receiver into choosing actions that are aligned with the sender's preference by selectively sharing information about the state. However, in contrast to the standard models, the sender does not know the prior, and has to persuade while gradually learning the prior on the fly. We study the sender's learning problem of making persuasive action recommendations to achieve low regret against the optimal persuasion mechanism with the knowledge of the prior distribution. Our main positive result is an algorithm that, with high probability, is persuasive across all rounds and achieves $O(\sqrt{T\log T})$ regret, where $T$ is the horizon length. The core philosophy behind the design of our algorithm is to leverage robustness against the sender's ignorance of the prior. Intuitively, at each time our algorithm maintains a set of candidate priors, and chooses a persuasion scheme that is simultaneously persuasive for all of them. To demonstrate the effectiveness of our algorithm, we further prove that no algorithm can achieve regret better than $\Omega(\sqrt{T})$, even if the persuasiveness requirements were significantly relaxed. Therefore, our algorithm achieves optimal regret for the sender's learning problem up to terms logarithmic in $T$.