An Improved Approach to Estimate the Internal Resistance of a Battery

This paper considers the problem of resistance estimation in electronic systems including battery management systems (BMS) and battery chargers. In typical applications, the battery resistance is obtained through an approximate method computed as the ratio of the voltage difference to the applied current excitation pulse or vice versa for admittance. When estimating the battery resistance, this approach ignores the change in the open circuit voltage (OCV) as a result of the excitation signal. In this paper, we formally demonstrate and quantify the effect of the OCV drop on the errors in internal resistance estimation. Then, we propose a novel method to accurately estimate the internal resistance by accounting for the change in OCV caused by the applied current excitation signal. The proposed approach is based on a novel observation model that allows one to estimate the effect of OCV without requiring any additional information, such as the state of charge (SOC), parameters of the OCV-SOC curve, and the battery capacity. As such, the proposed approach is independent of the battery chemistry, size, age, and the ambient temperature. A performance analysis of the proposed approach using the battery simulator shows significant performance gain in the range of 30% to more than 250% in percentage estimation error. Then, the proposed approach is applied for resistance estimation during the hybrid pulse power characterization (HPPC) of cylindrical Li-ion battery cells. Results from tested batteries show that the proposed approach reduced the overestimated internal resistance of the batteries by up to 20 m{\Omega}.

A Unified View of Algorithms for Path Planning Using Probabilistic Inference on Factor Graphs

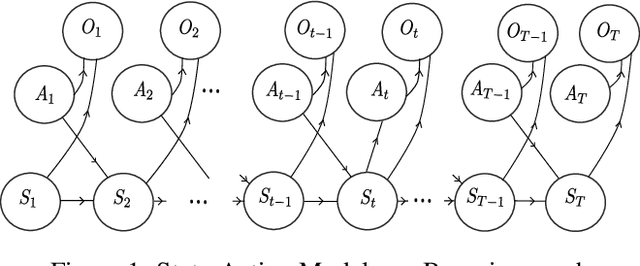
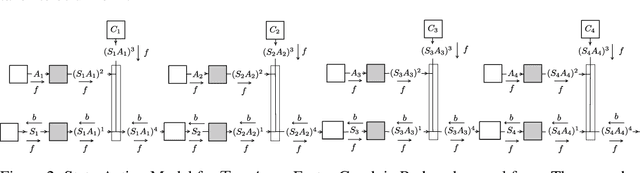
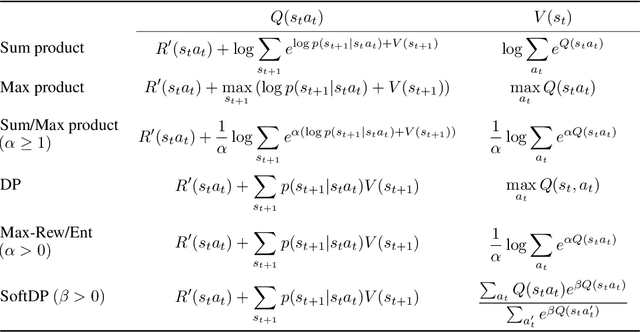
Even if path planning can be solved using standard techniques from dynamic programming and control, the problem can also be approached using probabilistic inference. The algorithms that emerge using the latter framework bear some appealing characteristics that qualify the probabilistic approach as a powerful alternative to the more traditional control formulations. The idea of using estimation on stochastic models to solve control problems is not new and the inference approach considered here falls under the rubric of Active Inference (AI) and Control as Inference (CAI). In this work, we look at the specific recursions that arise from various cost functions that, although they may appear similar in scope, bear noticeable differences, at least when applied to typical path planning problems. We start by posing the path planning problem on a probabilistic factor graph, and show how the various algorithms translate into specific message composition rules. We then show how this unified approach, presented both in probability space and in log space, provides a very general framework that includes the Sum-product, the Max-product, Dynamic programming and mixed Reward/Entropy criteria-based algorithms. The framework also expands algorithmic design options for smoother or sharper policy distributions, including generalized Sum/Max-product algorithm, a Smooth Dynamic programming algorithm and modified versions of the Reward/Entropy recursions. We provide a comprehensive table of recursions and a comparison through simulations, first on a synthetic small grid with a single goal with obstacles, and then on a grid extrapolated from a real-world scene with multiple goals and a semantic map.

Path Planning Using Probability Tensor Flows

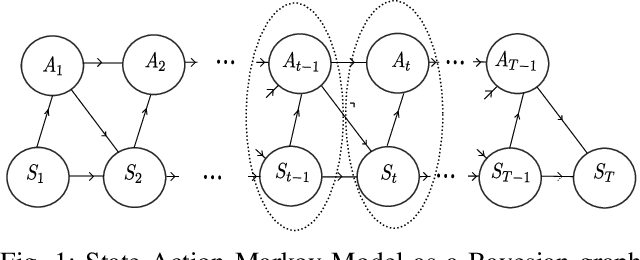
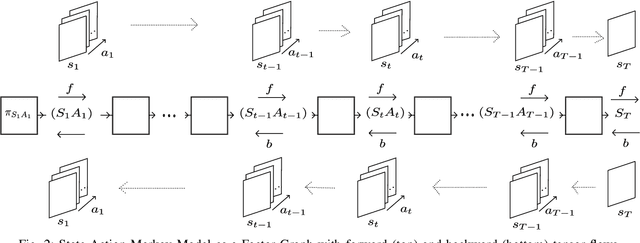
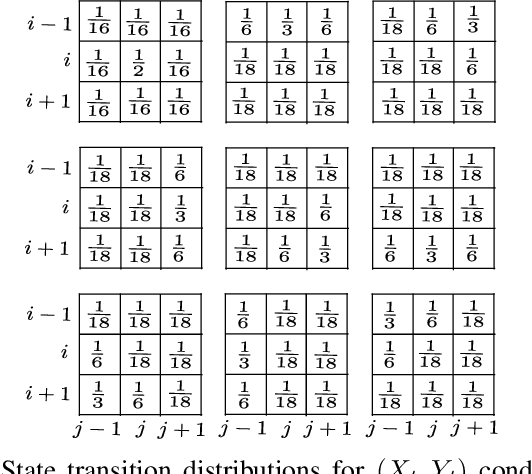
Probability models have been proposed in the literature to account for "intelligent" behavior in many contexts. In this paper, probability propagation is applied to model agent's motion in potentially complex scenarios that include goals and obstacles. The backward flow provides precious background information to the agent's behavior, viz., inferences coming from the future determine the agent's actions. Probability tensors are layered in time in both directions in a manner similar to convolutional neural networks. The discussion is carried out with reference to a set of simulated grids where, despite the apparent task complexity, a solution, if feasible, is always found. The original model proposed by Attias has been extended to include non-absorbing obstacles, multiple goals and multiple agents. The emerging behaviors are very realistic and demonstrate great potentials of the application of this framework to real environments.