AI-Augmented Density-Driven Optimal Control (D2OC) for Decentralized Environmental Mapping

This paper presents an AI-augmented decentralized framework for multi-agent (multi-robot) environmental mapping under limited sensing and communication. While conventional coverage formulations achieve effective spatial allocation when an accurate reference map is available, their performance deteriorates under uncertain or biased priors. The proposed method introduces an adaptive and self-correcting mechanism that enables agents to iteratively refine local density estimates within an optimal transport-based framework, ensuring theoretical consistency and scalability. A dual multilayer perceptron (MLP) module enhances adaptivity by inferring local mean-variance statistics and regulating virtual uncertainty for long-unvisited regions, mitigating stagnation around local minima. Theoretical analysis rigorously proves convergence under the Wasserstein metric, while simulation results demonstrate that the proposed AI-augmented Density-Driven Optimal Control consistently achieves robust and precise alignment with the ground-truth density, yielding substantially higher-fidelity reconstruction of complex multi-modal spatial distributions compared with conventional decentralized baselines.

Optimal Transport-Based Decentralized Multi-Agent Distribution Matching

This paper presents a decentralized control framework for distribution matching in multi-agent systems (MAS), where agents collectively achieve a prescribed terminal spatial distribution. The problem is formulated using optimal transport (Wasserstein distance), which provides a principled measure of distributional discrepancy and serves as the basis for the control design. To avoid solving the global optimal transport problem directly, the distribution-matching objective is reformulated into a tractable per-agent decision process, enabling each agent to identify its desired terminal locations using only locally available information. A sequential weight-update rule is introduced to construct feasible local transport plans, and a memory-based correction mechanism is incorporated to maintain reliable operation under intermittent and range-limited communication. Convergence guarantees are established, showing cycle-wise improvement of a surrogate transport cost under both linear and nonlinear agent dynamics. Simulation results demonstrate that the proposed framework achieves effective and scalable distribution matching while operating fully in a decentralized manner.

Breaking Symmetry-Induced Degeneracy in Multi-Agent Ergodic Coverage via Stochastic Spectral Control

Multi-agent ergodic coverage via Spectral Multiscale Coverage (SMC) provides a principled framework for driving a team of agents so that their collective time-averaged trajectories match a prescribed spatial distribution. While classical SMC has demonstrated empirical success, it can suffer from gradient cancellation, particularly when agents are initialized near symmetry points of the target distribution, leading to undesirable behaviors such as stalling or motion constrained along symmetry axes. In this work, we rigorously characterize the initial conditions and symmetry-induced invariant manifolds that give rise to such directional degeneracy in first-order agent dynamics. To address this, we introduce a stochastic perturbation combined with a contraction term and prove that the resulting dynamics ensure almost-sure escape from zero-gradient manifolds while maintaining mean-square boundedness of agent trajectories. Simulations on symmetric multi-modal reference distributions demonstrate that the proposed stochastic SMC effectively mitigates transient stalling and axis-constrained motion, while ensuring that all agent trajectories remain bounded within the domain.

Density-Driven Multi-Agent Coordination for Efficient Farm Coverage and Management in Smart Agriculture

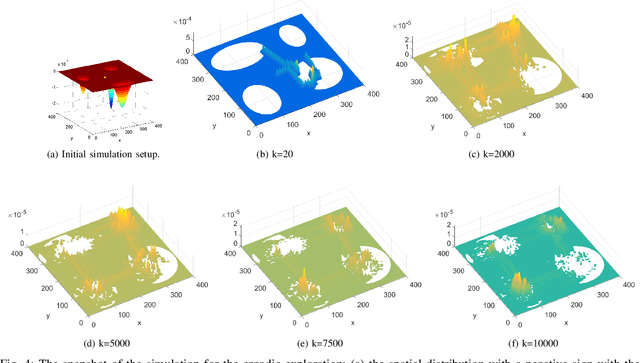
The growing scale of modern farms has increased the need for efficient and adaptive multi-agent coverage strategies for pest, weed, and disease management. Traditional methods such as manual inspection and blanket pesticide spraying often lead to excessive chemical use, resource waste, and environmental impact. While unmanned aerial vehicles (UAVs) offer a promising platform for precision agriculture through targeted spraying and improved operational efficiency, existing UAV-based approaches remain limited by battery life, payload capacity, and scalability, especially in large fields where single-UAV or uniformly distributed spraying is insufficient. Although multi-UAV coordination has been explored, many current frameworks still assume uniform spraying and do not account for infestation severity, UAV dynamics, non-uniform resource allocation, or energy-efficient coordination. To address these limitations, this paper proposes a Density-Driven Optimal Control (D2OC) framework that integrates Optimal Transport (OT) theory with multi-UAV coverage control for large-scale agricultural spraying. The method supports non-uniform, priority-aware resource allocation based on infestation intensity, reducing unnecessary chemical application. UAVs are modeled as a linear time-varying (LTV) system to capture variations in mass and inertia during spraying missions. The D2OC control law, derived using Lagrangian mechanics, enables efficient coordination, balanced workload distribution, and improved mission duration. Simulation results demonstrate that the proposed approach outperforms uniform spraying and Spectral Multiscale Coverage (SMC) in coverage efficiency, chemical reduction, and operational sustainability, providing a scalable solution for smart agriculture.

Density-Driven Optimal Control for Non-Uniform Area Coverage in Decentralized Multi-Agent Systems Using Optimal Transport

This paper addresses the fundamental problem of non-uniform area coverage in multi-agent systems, where different regions require varying levels of attention due to mission-dependent priorities. Existing uniform coverage strategies are insufficient for realistic applications, and many non-uniform approaches either lack optimality guarantees or fail to incorporate crucial real-world constraints such as agent dynamics, limited operation time, the number of agents, and decentralized execution. To resolve these limitations, we propose a novel framework called Density-Driven Optimal Control (D2OC). The central idea of D2OC is the integration of optimal transport theory with multi-agent coverage control, enabling each agent to continuously adjust its trajectory to match a mission-specific reference density map. The proposed formulation establishes optimality by solving a constrained optimization problem that explicitly incorporates physical and operational constraints. The resulting control input is analytically derived from the Lagrangian of the objective function, yielding closed-form optimal solutions for linear systems and a generalizable structure for nonlinear systems. Furthermore, a decentralized data-sharing mechanism is developed to coordinate agents without reliance on global information. Comprehensive simulation studies demonstrate that D2OC achieves significantly improved non-uniform area coverage performance compared to existing methods, while maintaining scalability and decentralized implementability.

Efficient, Decentralized, and Collaborative Multi-Robot Exploration using Optimal Transport Theory

An Optimal Transport (OT)-based decentralized collaborative multi-robot exploration strategy is proposed in this paper. This method is to achieve an efficient exploration with a predefined priority in the given domain. In this context, the efficiency indicates how a team of robots (agents) cover the domain reflecting the corresponding priority map (or degrees of importance) in the domain. The decentralized exploration implies that each agent carries out their exploration task independently in the absence of any supervisory agent/computer. When an agent encounters another agent within a communication range, each agent receives the information about which areas are already covered by other agents, yielding a collaborative exploration. The OT theory is employed to quantify the difference between the distribution formed by the robot trajectories and the given reference spatial distribution indicating the priority. A computationally feasible way is developed to measure the performance of the proposed exploration scheme. Further, the formal algorithm is provided for the efficient, decentralized, and collaborative exploration plan. Simulation results are presented to validate the proposed methods.

Ergodic Control Strategy for Multi-Agent Environment Exploration

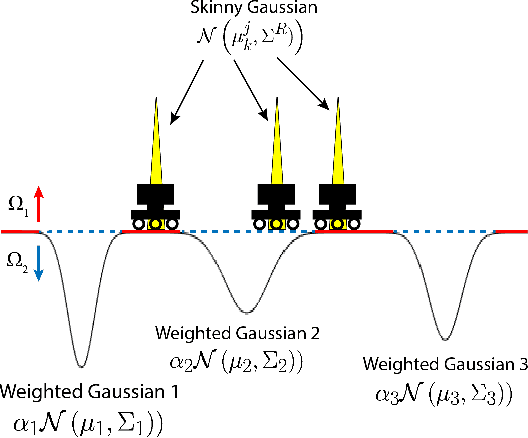
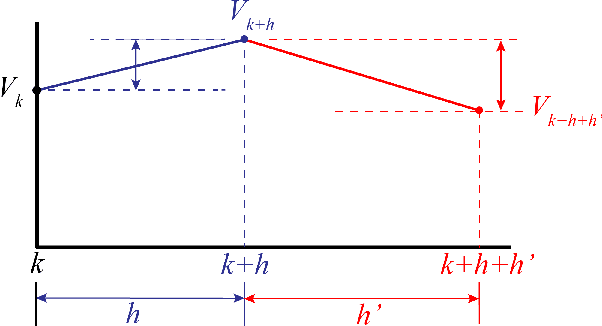
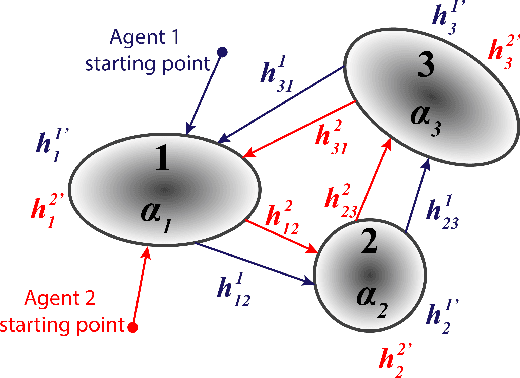
In this study, an ergodic environment exploration problem is introduced for a centralized multi-agent system. Given the reference distribution represented by the Mixture of Gaussian (MoG), the ergodicity is achieved when the time-averaged robot distribution is identical to the given reference distribution. The major challenge associated with this problem is to determine proper timing for a team of agents (robots) to visit each Gaussian component in the reference MoG for ergodicity. The ergodic function is defined as a measure of ergodicity and the condition for convergence is derived based on timing analysis. The proposed control strategy provides relatively reasonable performance to achieve the ergodicity. We provide the formal algorithm for centralized multi-agent control to achieve the ergodicity and simulation results are presented for the validation of the proposed algorithm.

Efficient Multi-Robot Exploration with Energy Constraint based on Optimal Transport Theory

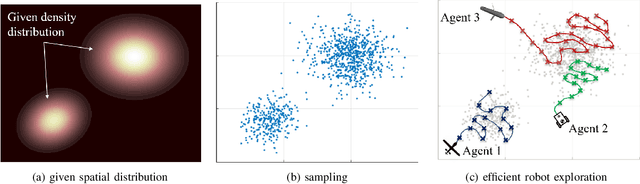
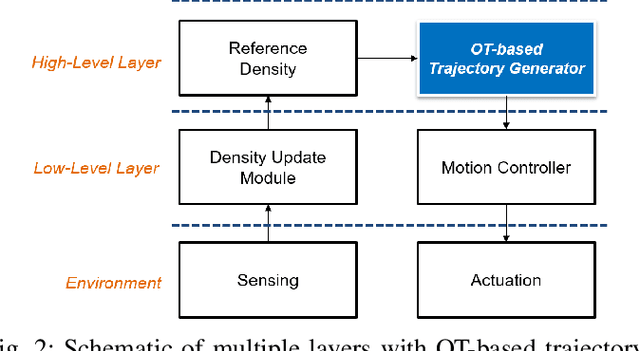
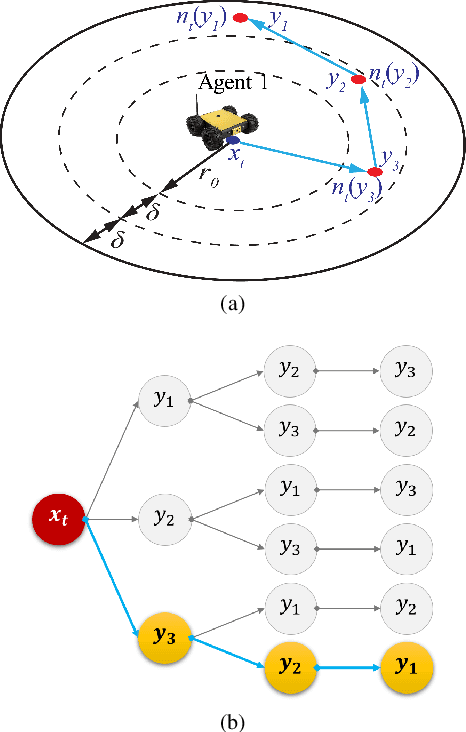
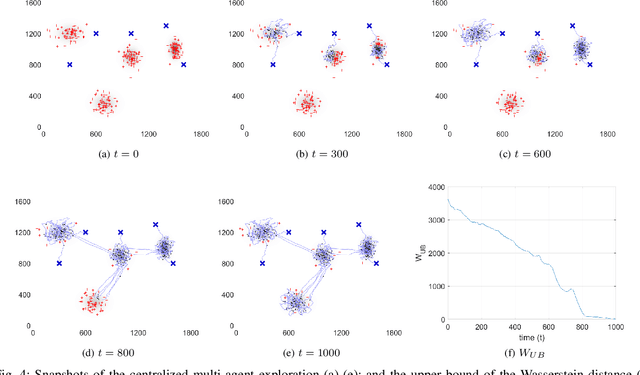
This paper addresses an Optimal Transport (OT)-based efficient multi-robot exploration problem, considering the energy constraints of a multi-robot system. The efficiency in this problem implies how a team of robots (agents) covers a given domain, reflecting a priority of areas of interest represented by a density distribution, rather than simply following a preset of uniform patterns. To achieve an efficient multi-robot exploration, the optimal transport theory that quantifies a distance between two density distributions is employed as a tool, which also serves as a means of performance measure. The energy constraints for the multi-robot system is then incorporated into the OT-based multi-robot exploration scheme. The proposed scheme is decoupled from robot dynamics, broadening the applicability of the multi-robot exploration plan to heterogeneous robot platforms. Not only the centralized but also decentralized algorithms are provided to cope with more realistic scenarios such as communication range limits between agents. To measure the exploration efficiency, the upper bound of the performance is developed for both the centralized and decentralized cases based on the optimal transport theory, which is computationally tractable as well as efficient. The proposed multi-robot exploration scheme is also applicable to a time-varying distribution, where the spatio-temporal evolution of the given reference distribution is desired. To validate the proposed method, multiple simulation results are provided.