LLM Meets Diffusion: A Hybrid Framework for Crystal Material Generation

Recent advances in generative modeling have shown significant promise in designing novel periodic crystal structures. Existing approaches typically rely on either large language models (LLMs) or equivariant denoising models, each with complementary strengths: LLMs excel at handling discrete atomic types but often struggle with continuous features such as atomic positions and lattice parameters, while denoising models are effective at modeling continuous variables but encounter difficulties in generating accurate atomic compositions. To bridge this gap, we propose CrysLLMGen, a hybrid framework that integrates an LLM with a diffusion model to leverage their complementary strengths for crystal material generation. During sampling, CrysLLMGen first employs a fine-tuned LLM to produce an intermediate representation of atom types, atomic coordinates, and lattice structure. While retaining the predicted atom types, it passes the atomic coordinates and lattice structure to a pre-trained equivariant diffusion model for refinement. Our framework outperforms state-of-the-art generative models across several benchmark tasks and datasets. Specifically, CrysLLMGen not only achieves a balanced performance in terms of structural and compositional validity but also generates more stable and novel materials compared to LLM-based and denoisingbased models Furthermore, CrysLLMGen exhibits strong conditional generation capabilities, effectively producing materials that satisfy user-defined constraints. Code is available at https://github.com/kdmsit/crysllmgen

CrysGNN : Distilling pre-trained knowledge to enhance property prediction for crystalline materials

In recent years, graph neural network (GNN) based approaches have emerged as a powerful technique to encode complex topological structure of crystal materials in an enriched representation space. These models are often supervised in nature and using the property-specific training data, learn relationship between crystal structure and different properties like formation energy, bandgap, bulk modulus, etc. Most of these methods require a huge amount of property-tagged data to train the system which may not be available for different properties. However, there is an availability of a huge amount of crystal data with its chemical composition and structural bonds. To leverage these untapped data, this paper presents CrysGNN, a new pre-trained GNN framework for crystalline materials, which captures both node and graph level structural information of crystal graphs using a huge amount of unlabelled material data. Further, we extract distilled knowledge from CrysGNN and inject into different state of the art property predictors to enhance their property prediction accuracy. We conduct extensive experiments to show that with distilled knowledge from the pre-trained model, all the SOTA algorithms are able to outperform their own vanilla version with good margins. We also observe that the distillation process provides a significant improvement over the conventional approach of finetuning the pre-trained model. We have released the pre-trained model along with the large dataset of 800K crystal graph which we carefully curated; so that the pretrained model can be plugged into any existing and upcoming models to enhance their prediction accuracy.

Line Hypergraph Convolution Network: Applying Graph Convolution for Hypergraphs

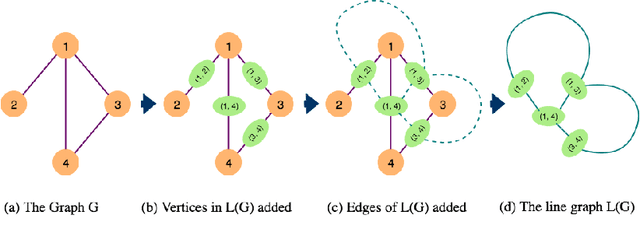
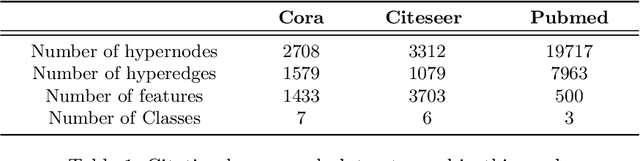
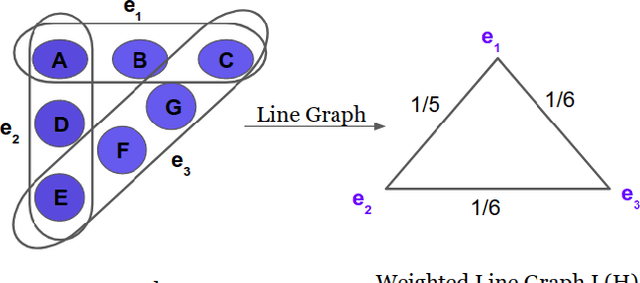
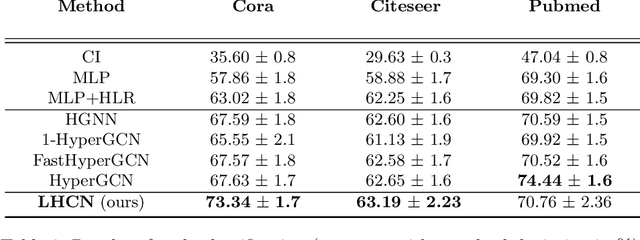
Network representation learning and node classification in graphs got significant attention due to the invent of different types graph neural networks. Graph convolution network (GCN) is a popular semi-supervised technique which aggregates attributes within the neighborhood of each node. Conventional GCNs can be applied to simple graphs where each edge connects only two nodes. But many modern days applications need to model high order relationships in a graph. Hypergraphs are effective data types to handle such complex relationships. In this paper, we propose a novel technique to apply graph convolution on hypergraphs with variable hyperedge sizes. We use the classical concept of line graph of a hypergraph for the first time in the hypergraph learning literature. Then we propose to use graph convolution on the line graph of a hypergraph. Experimental analysis on multiple real world network datasets shows the merit of our approach compared to state-of-the-arts.