Weight-Parameterization in Continuous Time Deep Neural Networks for Surrogate Modeling

Continuous-time deep learning models, such as neural ordinary differential equations (ODEs), offer a promising framework for surrogate modeling of complex physical systems. A central challenge in training these models lies in learning expressive yet stable time-varying weights, particularly under computational constraints. This work investigates weight parameterization strategies that constrain the temporal evolution of weights to a low-dimensional subspace spanned by polynomial basis functions. We evaluate both monomial and Legendre polynomial bases within neural ODE and residual network (ResNet) architectures under discretize-then-optimize and optimize-then-discretize training paradigms. Experimental results across three high-dimensional benchmark problems show that Legendre parameterizations yield more stable training dynamics, reduce computational cost, and achieve accuracy comparable to or better than both monomial parameterizations and unconstrained weight models. These findings elucidate the role of basis choice in time-dependent weight parameterization and demonstrate that using orthogonal polynomial bases offers a favorable tradeoff between model expressivity and training efficiency.

Polynomial Chaos Surrogate Construction for Random Fields with Parametric Uncertainty

Engineering and applied science rely on computational experiments to rigorously study physical systems. The mathematical models used to probe these systems are highly complex, and sampling-intensive studies often require prohibitively many simulations for acceptable accuracy. Surrogate models provide a means of circumventing the high computational expense of sampling such complex models. In particular, polynomial chaos expansions (PCEs) have been successfully used for uncertainty quantification studies of deterministic models where the dominant source of uncertainty is parametric. We discuss an extension to conventional PCE surrogate modeling to enable surrogate construction for stochastic computational models that have intrinsic noise in addition to parametric uncertainty. We develop a PCE surrogate on a joint space of intrinsic and parametric uncertainty, enabled by Rosenblatt transformations, and then extend the construction to random field data via the Karhunen-Loeve expansion. We then take advantage of closed-form solutions for computing PCE Sobol indices to perform a global sensitivity analysis of the model which quantifies the intrinsic noise contribution to the overall model output variance. Additionally, the resulting joint PCE is generative in the sense that it allows generating random realizations at any input parameter setting that are statistically approximately equivalent to realizations from the underlying stochastic model. The method is demonstrated on a chemical catalysis example model.

Compressive sensing adaptation for polynomial chaos expansions

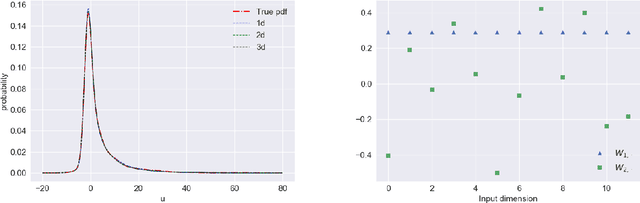
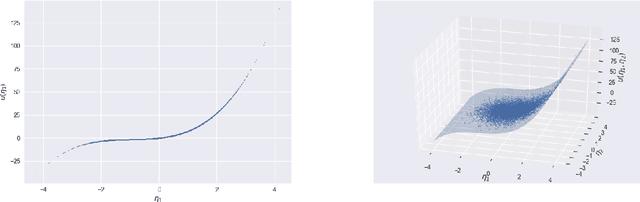
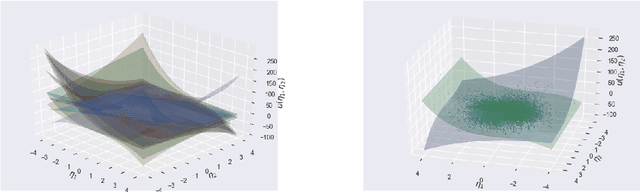
Basis adaptation in Homogeneous Chaos spaces rely on a suitable rotation of the underlying Gaussian germ. Several rotations have been proposed in the literature resulting in adaptations with different convergence properties. In this paper we present a new adaptation mechanism that builds on compressive sensing algorithms, resulting in a reduced polynomial chaos approximation with optimal sparsity. The developed adaptation algorithm consists of a two-step optimization procedure that computes the optimal coefficients and the input projection matrix of a low dimensional chaos expansion with respect to an optimally rotated basis. We demonstrate the attractive features of our algorithm through several numerical examples including the application on Large-Eddy Simulation (LES) calculations of turbulent combustion in a HIFiRE scramjet engine.