Implicit Interpretation of Importance Weight Aware Updates

Due to its speed and simplicity, subgradient descent is one of the most used optimization algorithms in convex machine learning algorithms. However, tuning its learning rate is probably its most severe bottleneck to achieve consistent good performance. A common way to reduce the dependency on the learning rate is to use implicit/proximal updates. One such variant is the Importance Weight Aware (IWA) updates, which consist of infinitely many infinitesimal updates on each loss function. However, IWA updates' empirical success is not completely explained by their theory. In this paper, we show for the first time that IWA updates have a strictly better regret upper bound than plain gradient updates in the online learning setting. Our analysis is based on the new framework, generalized implicit Follow-the-Regularized-Leader (FTRL) (Chen and Orabona, 2023), to analyze generalized implicit updates using a dual formulation. In particular, our results imply that IWA updates can be considered as approximate implicit/proximal updates.

Generalized Implicit Follow-The-Regularized-Leader

We propose a new class of online learning algorithms, generalized implicit Follow-The-Regularized-Leader (FTRL), that expands the scope of FTRL framework. Generalized implicit FTRL can recover known algorithms, as FTRL with linearized losses and implicit FTRL, and it allows the design of new update rules, as extensions of aProx and Mirror-Prox to FTRL. Our theory is constructive in the sense that it provides a simple unifying framework to design updates that directly improve the worst-case upper bound on the regret. The key idea is substituting the linearization of the losses with a Fenchel-Young inequality. We show the flexibility of the framework by proving that some known algorithms, like the Mirror-Prox updates, are instantiations of the generalized implicit FTRL. Finally, the new framework allows us to recover the temporal variation bound of implicit OMD, with the same computational complexity.

Implicit Parameter-free Online Learning with Truncated Linear Models

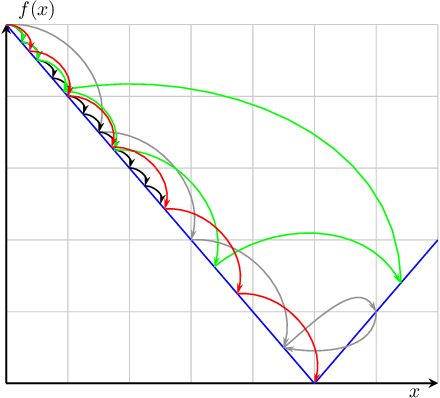
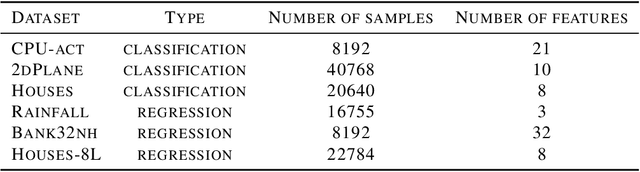
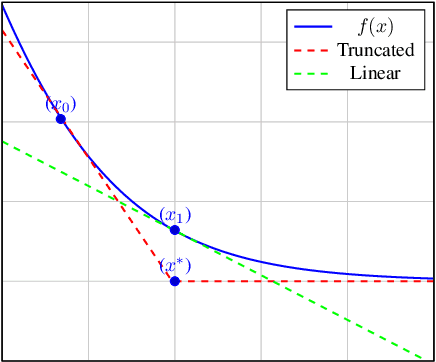
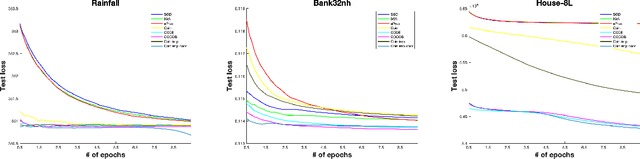
Parameter-free algorithms are online learning algorithms that do not require setting learning rates. They achieve optimal regret with respect to the distance between the initial point and any competitor. Yet, parameter-free algorithms do not take into account the geometry of the losses. Recently, in the stochastic optimization literature, it has been proposed to instead use truncated linear lower bounds, which produce better performance by more closely modeling the losses. In particular, truncated linear models greatly reduce the problem of overshooting the minimum of the loss function. Unfortunately, truncated linear models cannot be used with parameter-free algorithms because the updates become very expensive to compute. In this paper, we propose new parameter-free algorithms that can take advantage of truncated linear models through a new update that has an "implicit" flavor. Based on a novel decomposition of the regret, the new update is efficient, requires only one gradient at each step, never overshoots the minimum of the truncated model, and retains the favorable parameter-free properties. We also conduct an empirical study demonstrating the practical utility of our algorithms.

Better Parameter-free Stochastic Optimization with ODE Updates for Coin-Betting

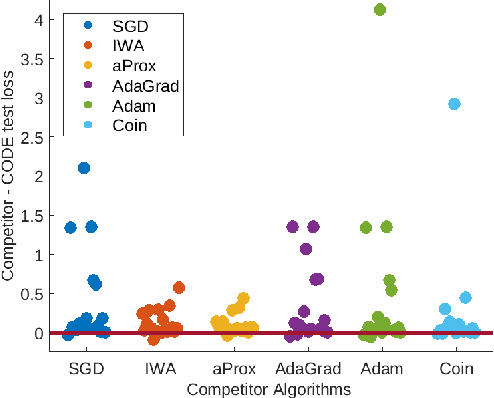
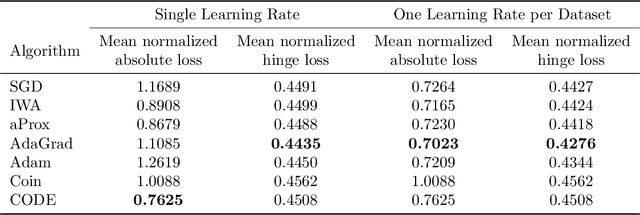
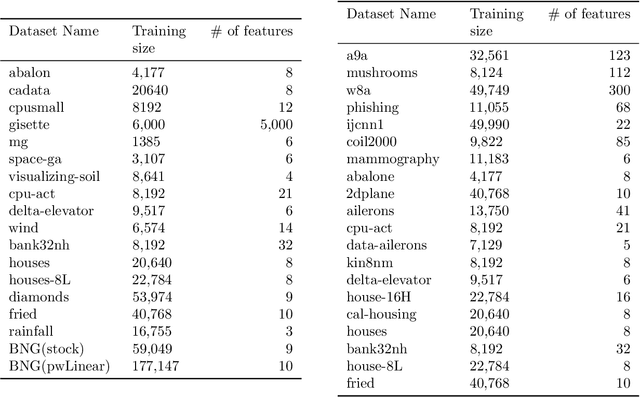
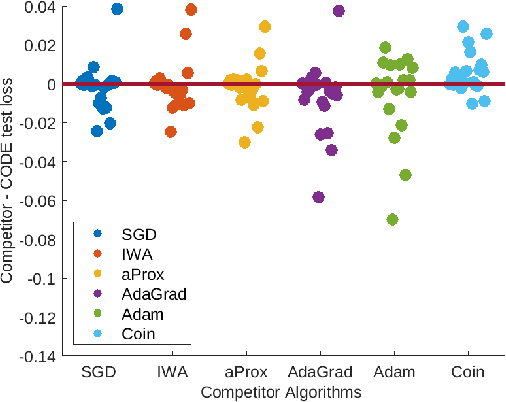
Parameter-free stochastic gradient descent (PFSGD) algorithms do not require setting learning rates while achieving optimal theoretical performance. In practical applications, however, there remains an empirical gap between tuned stochastic gradient descent (SGD) and PFSGD. In this paper, we close the empirical gap with a new parameter-free algorithm based on continuous-time Coin-Betting on truncated models. The new update is derived through the solution of an Ordinary Differential Equation (ODE) and solved in a closed form. We show empirically that this new parameter-free algorithm outperforms algorithms with the "best default" learning rates and almost matches the performance of finely tuned baselines without anything to tune.