Estimation of Stationary Optimal Transport Plans

We study optimal transport problems in which finite-valued quantities of interest evolve dynamically over time in a stationary fashion. Mathematically, this is a special case of the general optimal transport problem in which the distributions under study represent stationary processes and the cost depends on a finite number of time points. In this setting, we argue that one should restrict attention to stationary couplings, also known as joinings, which have close connections with long run average cost. We introduce estimators of both optimal joinings and the optimal joining cost, and we establish their consistency under mild conditions. Under stronger mixing assumptions we establish finite-sample error rates for the same estimators that extend the best known results in the iid case. Finally, we extend the consistency and rate analysis to an entropy-penalized version of the optimal joining problem.

Graph Optimal Transport with Transition Couplings of Random Walks

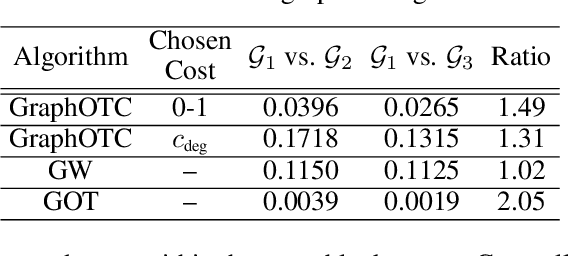
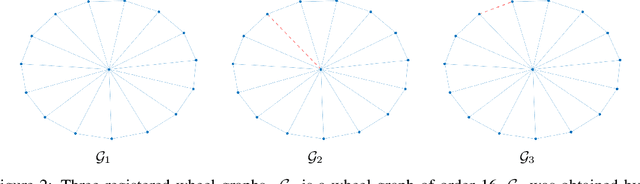
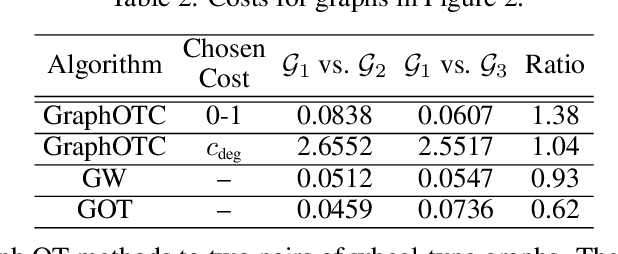
We present a novel approach to optimal transport between graphs from the perspective of stationary Markov chains. A weighted graph may be associated with a stationary Markov chain by means of a random walk on the vertex set with transition distributions depending on the edge weights of the graph. After drawing this connection, we describe how optimal transport techniques for stationary Markov chains may be used in order to perform comparison and alignment of the graphs under study. In particular, we propose the graph optimal transition coupling problem, referred to as GraphOTC, in which the Markov chains associated to two given graphs are optimally synchronized to minimize an expected cost. The joint synchronized chain yields an alignment of the vertices and edges in the two graphs, and the expected cost of the synchronized chain acts as a measure of distance or dissimilarity between the two graphs. We demonstrate that GraphOTC performs equal to or better than existing state-of-the-art techniques in graph optimal transport for several tasks and datasets. Finally, we also describe a generalization of the GraphOTC problem, called the FusedOTC problem, from which we recover the GraphOTC and OT costs as special cases.