Graph Optimal Transport with Transition Couplings of Random Walks

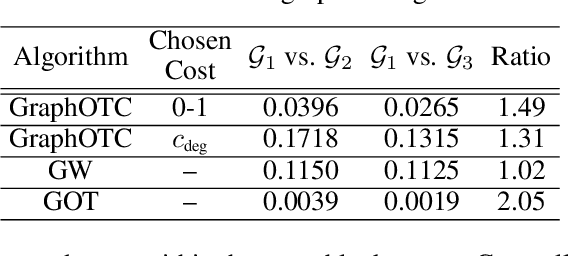
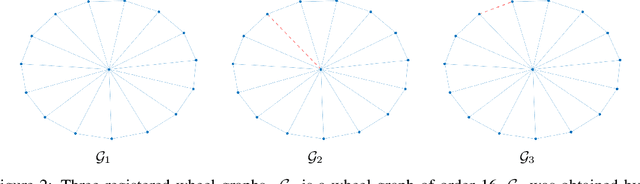
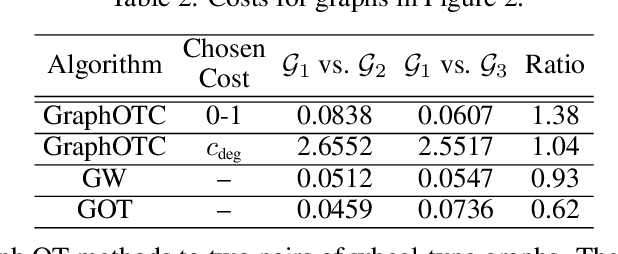
We present a novel approach to optimal transport between graphs from the perspective of stationary Markov chains. A weighted graph may be associated with a stationary Markov chain by means of a random walk on the vertex set with transition distributions depending on the edge weights of the graph. After drawing this connection, we describe how optimal transport techniques for stationary Markov chains may be used in order to perform comparison and alignment of the graphs under study. In particular, we propose the graph optimal transition coupling problem, referred to as GraphOTC, in which the Markov chains associated to two given graphs are optimally synchronized to minimize an expected cost. The joint synchronized chain yields an alignment of the vertices and edges in the two graphs, and the expected cost of the synchronized chain acts as a measure of distance or dissimilarity between the two graphs. We demonstrate that GraphOTC performs equal to or better than existing state-of-the-art techniques in graph optimal transport for several tasks and datasets. Finally, we also describe a generalization of the GraphOTC problem, called the FusedOTC problem, from which we recover the GraphOTC and OT costs as special cases.

Joint and individual variation explained (JIVE) for integrated analysis of multiple data types

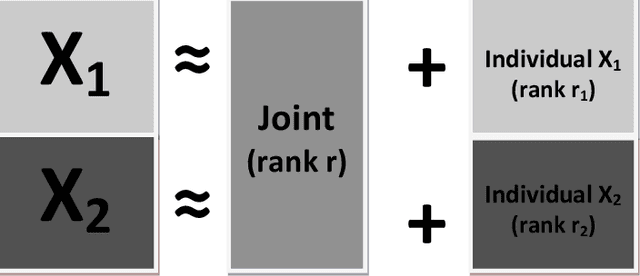
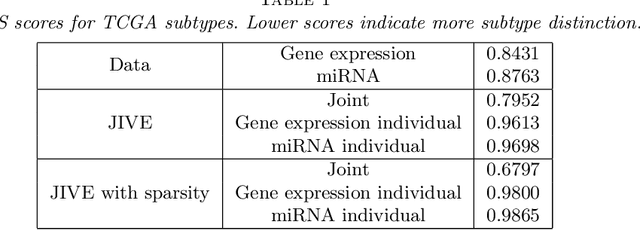
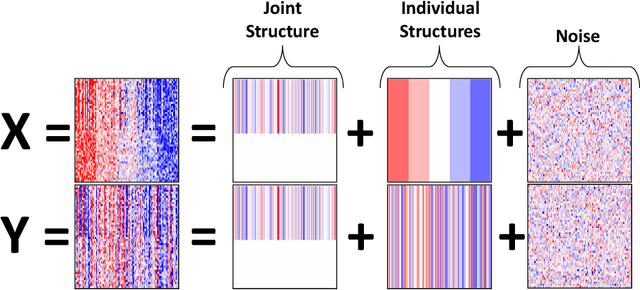
Research in several fields now requires the analysis of data sets in which multiple high-dimensional types of data are available for a common set of objects. In particular, The Cancer Genome Atlas (TCGA) includes data from several diverse genomic technologies on the same cancerous tumor samples. In this paper we introduce Joint and Individual Variation Explained (JIVE), a general decomposition of variation for the integrated analysis of such data sets. The decomposition consists of three terms: a low-rank approximation capturing joint variation across data types, low-rank approximations for structured variation individual to each data type, and residual noise. JIVE quantifies the amount of joint variation between data types, reduces the dimensionality of the data and provides new directions for the visual exploration of joint and individual structures. The proposed method represents an extension of Principal Component Analysis and has clear advantages over popular two-block methods such as Canonical Correlation Analysis and Partial Least Squares. A JIVE analysis of gene expression and miRNA data on Glioblastoma Multiforme tumor samples reveals gene-miRNA associations and provides better characterization of tumor types. Data and software are available at https://genome.unc.edu/jive/

Uniform Approximation of Vapnik-Chervonenkis Classes

For any family of measurable sets in a probability space, we show that either (i) the family has infinite Vapnik-Chervonenkis (VC) dimension or (ii) for every epsilon > 0 there is a finite partition pi such the pi-boundary of each set has measure at most epsilon. Immediate corollaries include the fact that a family with finite VC dimension has finite bracketing numbers, and satisfies uniform laws of large numbers for every ergodic process. From these corollaries, we derive analogous results for VC major and VC graph families of functions.

Uniform Approximation and Bracketing Properties of VC classes

We show that the sets in a family with finite VC dimension can be uniformly approximated within a given error by a finite partition. Immediate corollaries include the fact that VC classes have finite bracketing numbers, satisfy uniform laws of averages under strong dependence, and exhibit uniform mixing. Our results are based on recent work concerning uniform laws of averages for VC classes under ergodic sampling.

The Gap Dimension and Uniform Laws of Large Numbers for Ergodic Processes

Let F be a family of Borel measurable functions on a complete separable metric space. The gap (or fat-shattering) dimension of F is a combinatorial quantity that measures the extent to which functions f in F can separate finite sets of points at a predefined resolution gamma > 0. We establish a connection between the gap dimension of F and the uniform convergence of its sample averages under ergodic sampling. In particular, we show that if the gap dimension of F at resolution gamma > 0 is finite, then for every ergodic process the sample averages of functions in F are eventually within 10 gamma of their limiting expectations uniformly over the class F. If the gap dimension of F is finite for every resolution gamma > 0 then the sample averages of functions in F converge uniformly to their limiting expectations. We assume only that F is uniformly bounded and countable (or countably approximable). No smoothness conditions are placed on F, and no assumptions beyond ergodicity are placed on the sampling processes. Our results extend existing work for i.i.d. processes.